A simple pendulum of length L and mass m has a spring of force constant k connected to it at a distance h below its point of suspension. Find the frequency of vibrations of the system for small values of amplitude.

Let pendulum is given a small angular displacement θ,

Torque about O, τ=mgLsinθ+kxh
=mgLsinθ+kh2tanθ
For small θ, sinθ_-^~tantheta_−~θ
τ=−(mgL+kh2)θ
Iα=−(mgL+kh2)θ
α=−(mgL+kh2mL2)θ=−ω2θ
f=12π√mgL+kh2mL2
Topper's Solved these Questions
Similar Questions
On suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :

View SolutionA block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View Solution
Knowledge Check
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mkA pendulam of length L and bob of mass M has a speing of force constant K connected a speing of force constsnt K connected horizontally to it at a distance h below is point of suspension. The rod is in equilibrium in vertical podition. The rod of length L. used for vertical suspension s rigid and massless. The frequency of vibration of the system for small values of θ is
 A12πL√gL+khmB12πL√mgL+kmC2π√kL2mgL+khD12πL√gL+kh2m
A12πL√gL+khmB12πL√mgL+kmC2π√kL2mgL+khD12πL√gL+kh2m
A simple pendulum length l with a bob of mass m is taken into Earth orbit on the International space station. What is its frequency of oscillation with respect to that on the ground?
View SolutionTwo identical springs, each of force constant k are connected I (a) series (b) parallel and they support a mass M. Calculate the ratio of the frequency of oscillation of the mass in two systems.
View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
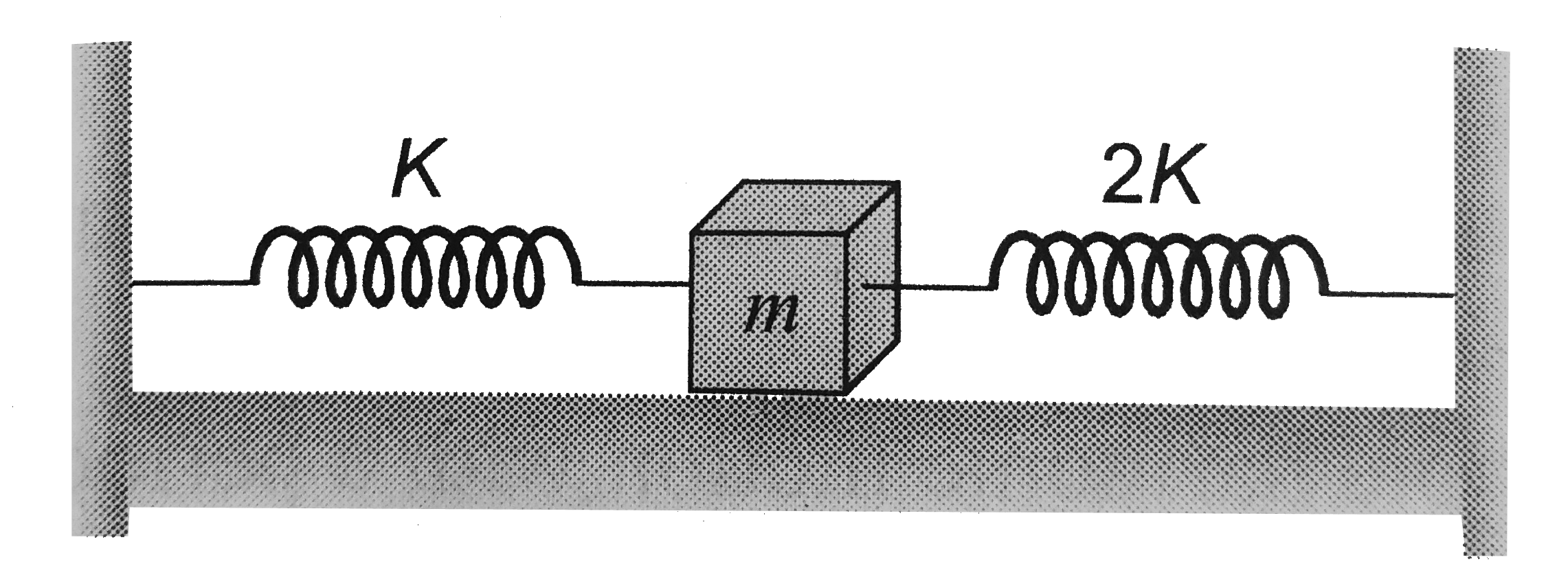
View SolutionA spring of force constant k is cut into two equal parts, and mass 'm' is suspended from parallel combination of the springs. Then frequency of small osciollations is
View SolutionA simple pendulum of length l and mass m is initially at its lowest position. It is given the minimum horizontal speed necessary after to move in a circular path about the point of suspension. The tension in the string at the lowest positive of the bob is
View Solution