The masses (M+m) and (M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are relased from rest the acceleraion of the system is .
gm/M
2gM/m
gm/2M
g(M2−m2)/2M
The correct Answer is:A
To solve the problem of finding the acceleration of the system with masses (M+m) and (M−m) attached to a light inextensible string over a smooth fixed pulley, we will follow these steps:
Step 1: Identify the masses
Let:
- M1=M+m (the mass on one side of the pulley)
- M2=M−m (the mass on the other side of the pulley)
Step 2: Write the equations of motion
For mass M1 (which is M+m):
- The force acting downwards is M1g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
M1g−T=M1a(1)
For mass M2 (which is M−m):
- The force acting downwards is M2g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
T−M2g=M2a(2)
Step 3: Substitute the masses into the equations
Substituting M1 and M2 into equations (1) and (2):
1. For M1:
(M+m)g−T=(M+m)a(3)
2. For M2:
T−(M−m)g=(M−m)a(4)
Step 4: Add equations (3) and (4)
Adding equations (3) and (4) to eliminate T:
(M+m)g−T+T−(M−m)g=(M+m)a+(M−m)a
This simplifies to:
(M+m)g−(M−m)g=(M+m+M−m)a
(2m)g=(2M)a
Step 5: Solve for acceleration a
Now, we can isolate a:
a=(2m)g(2M)=mgM
Final Answer
Thus, the acceleration of the system is:
a=mgM
Let:
- M1=M+m (the mass on one side of the pulley)
- M2=M−m (the mass on the other side of the pulley)
For mass M1 (which is M+m):
- The force acting downwards is M1g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
M1g−T=M1a(1)
- The force acting downwards is M2g (weight).
- The force acting upwards is the tension T.
- According to Newton's second law:
T−M2g=M2a(2)
Substituting M1 and M2 into equations (1) and (2):
1. For M1:
(M+m)g−T=(M+m)a(3)
2. For M2:
T−(M−m)g=(M−m)a(4)
Adding equations (3) and (4) to eliminate T:
(M+m)g−T+T−(M−m)g=(M+m)a+(M−m)a
This simplifies to:
(M+m)g−(M−m)g=(M+m+M−m)a
(2m)g=(2M)a
Now, we can isolate a:
a=(2m)g(2M)=mgM
Thus, the acceleration of the system is:
a=mgM
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -II (C.W)71videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III31videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - C.U.Q73videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
Similar Questions
Two uneqal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
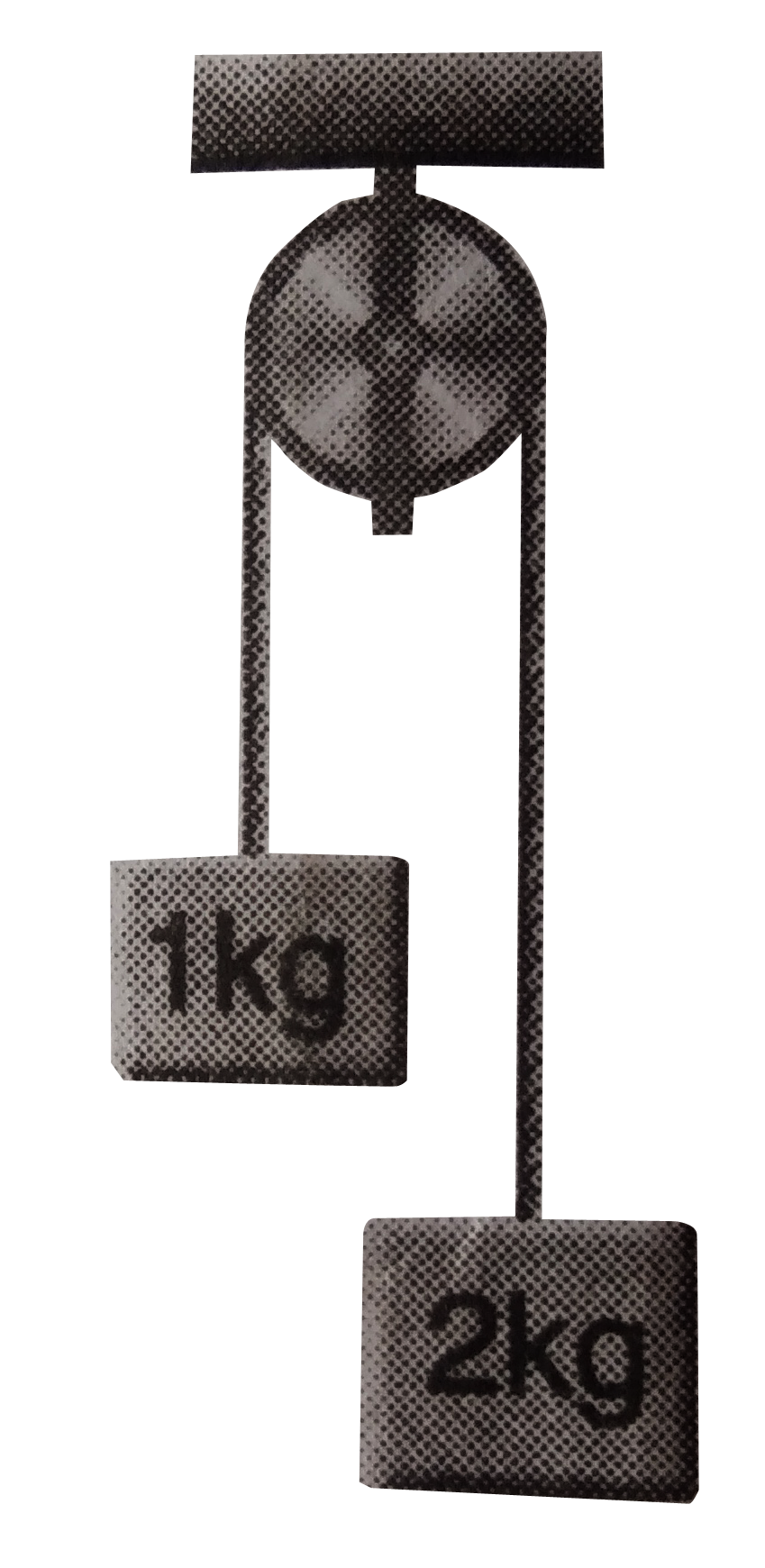 View Solution
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)
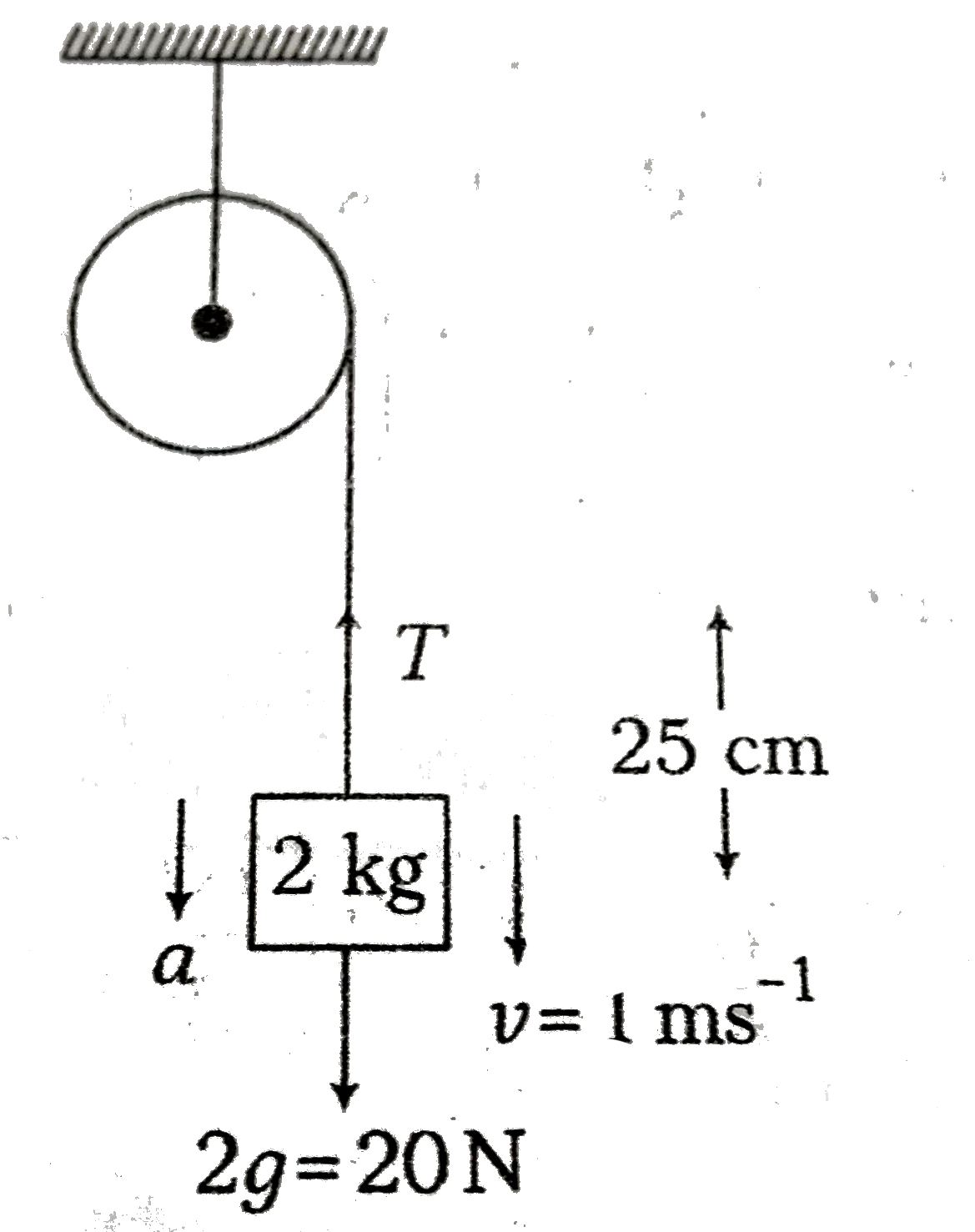 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
Agm/MB2gM/mCgm/2MDg(M2−m2)/2M - Question 2 - Select One
Two masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
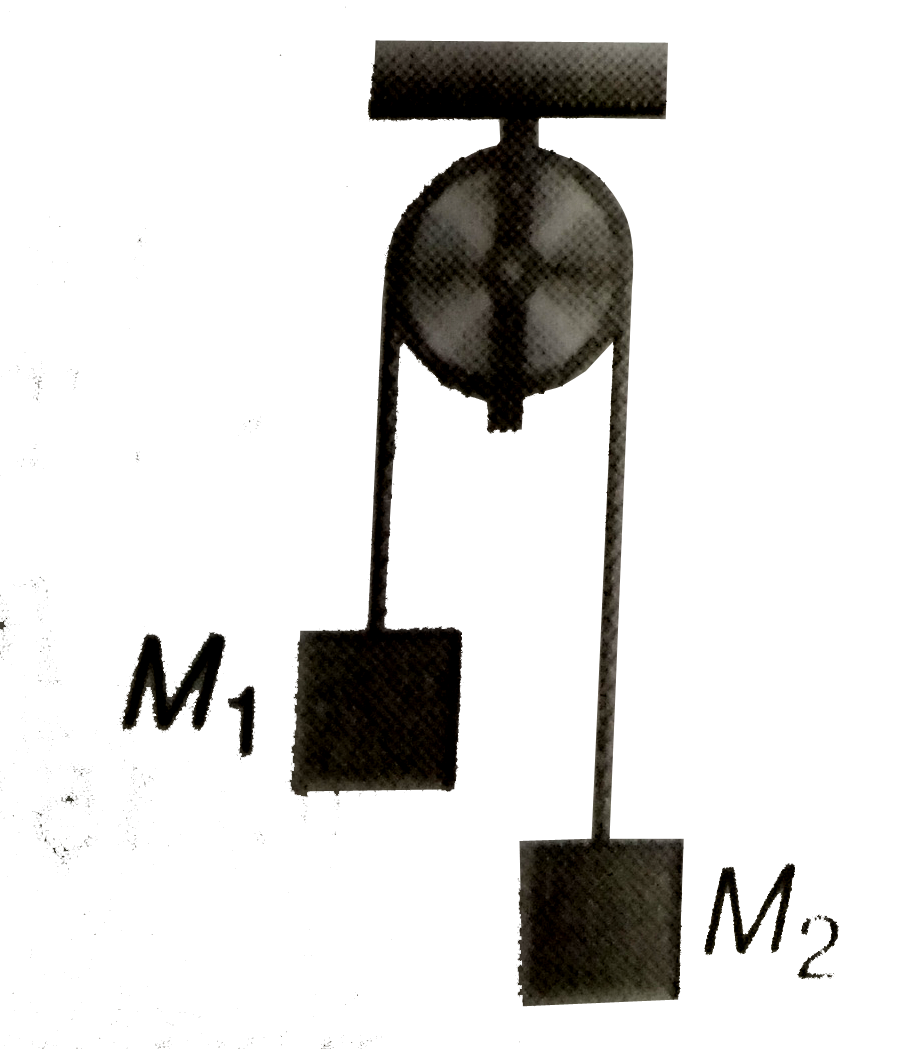 AgBg/2Cg/3Dg/4
AgBg/2Cg/3Dg/4 - Question 3 - Select One
Two particles of mass m1 and m2(m1>m2) are attached to the ends of a light inextensible string passing over a smooth fixed pulley. When the level of m1 is higher than that of m2 by 49 cm and string is just taut m2 is released. 0.5 s after motion started the masses are at the same level. the ratio of m1 to m2 is (Take g=9.8ms−2)
A7:3B4:3C3:2D2:1
Two masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionTwo blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
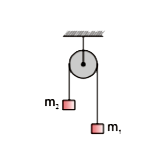 View Solution
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
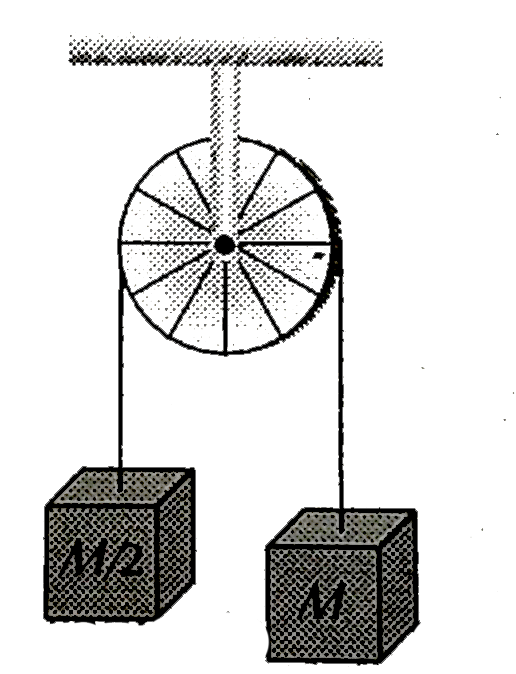 View Solution
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
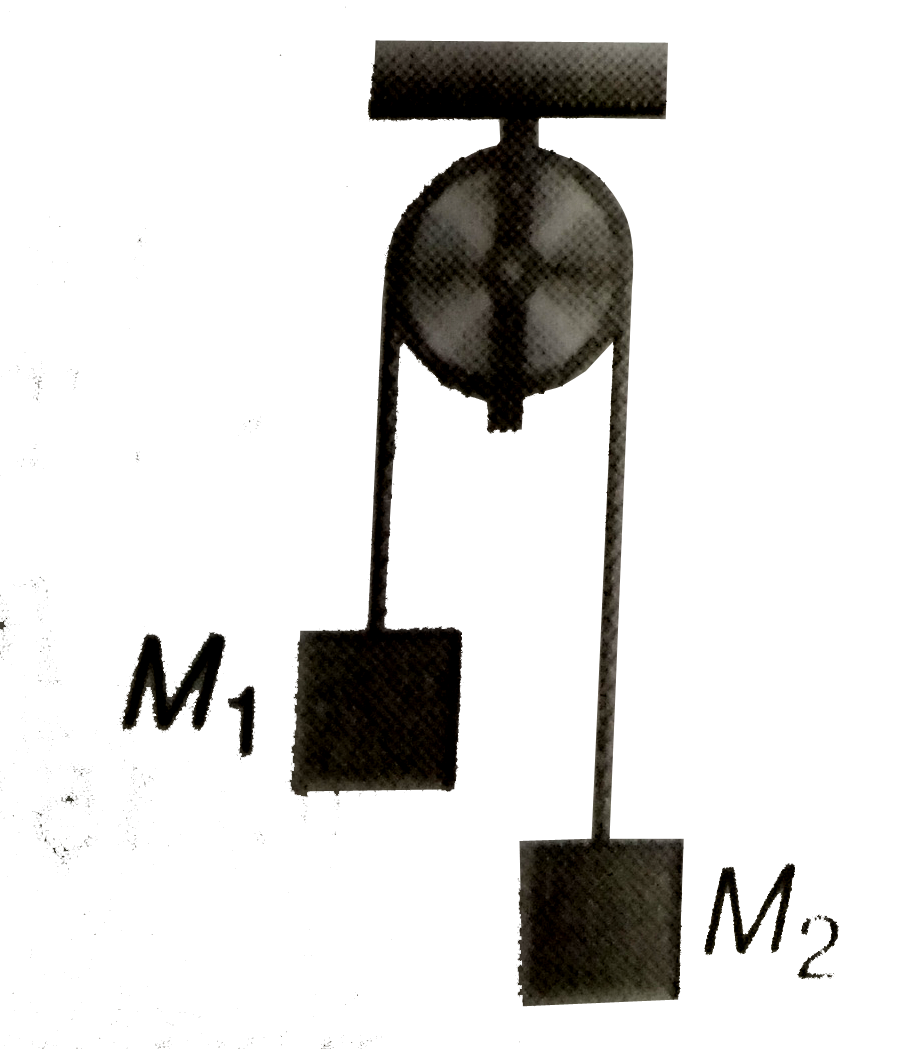 View Solution
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View Solution

