A particle of mass m , initially at rest , is acted upon by a variable force F for a brief interval of time T. It begins to move with a velocity u after the force stops acting . F is shown in the graph as a function of time. The curve is a semicircle.

u=πF202m
u=πT28m
u=πF0T4m
u=πF0T2m
The correct Answer is:C
Impulse = Area of semi circle .
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III31videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION33videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -I (C.W)47videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
Similar Questions
A particle of mass 2 kg is initially at rest. A force , acts on it whose magnitude changes with time. The force-time graph is of shown here.
The velocity of the particle after 10 s is
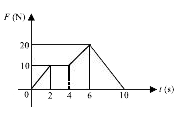 View Solution
View SolutionA particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AF2t2mBF2t22mCF2t23mDFt2m - Question 2 - Select One
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
AF2t2mBF2t22mCF2t23mDFt2m - Question 3 - Select One
A particle of mass m at rest is acted upon by a force P for a time t. Its kinetic energy after an interval t is
Ap2t2mBp2t22mCp2t23mDpt2m
A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA particle of mass 'm' and initially at rest is acted by a force F=a t. Newtons best representation of force-displacement graph is:
View SolutionA particle of mas 70g, moving at 50cm/sis acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t.
 View Solution
View SolutionA particle of mass m initially at rest is acted upon by a unidirectional force F=F∘cos(π2t). The distance travelled by the particle when it stops first in the subsequent motion is ,
View Solution

