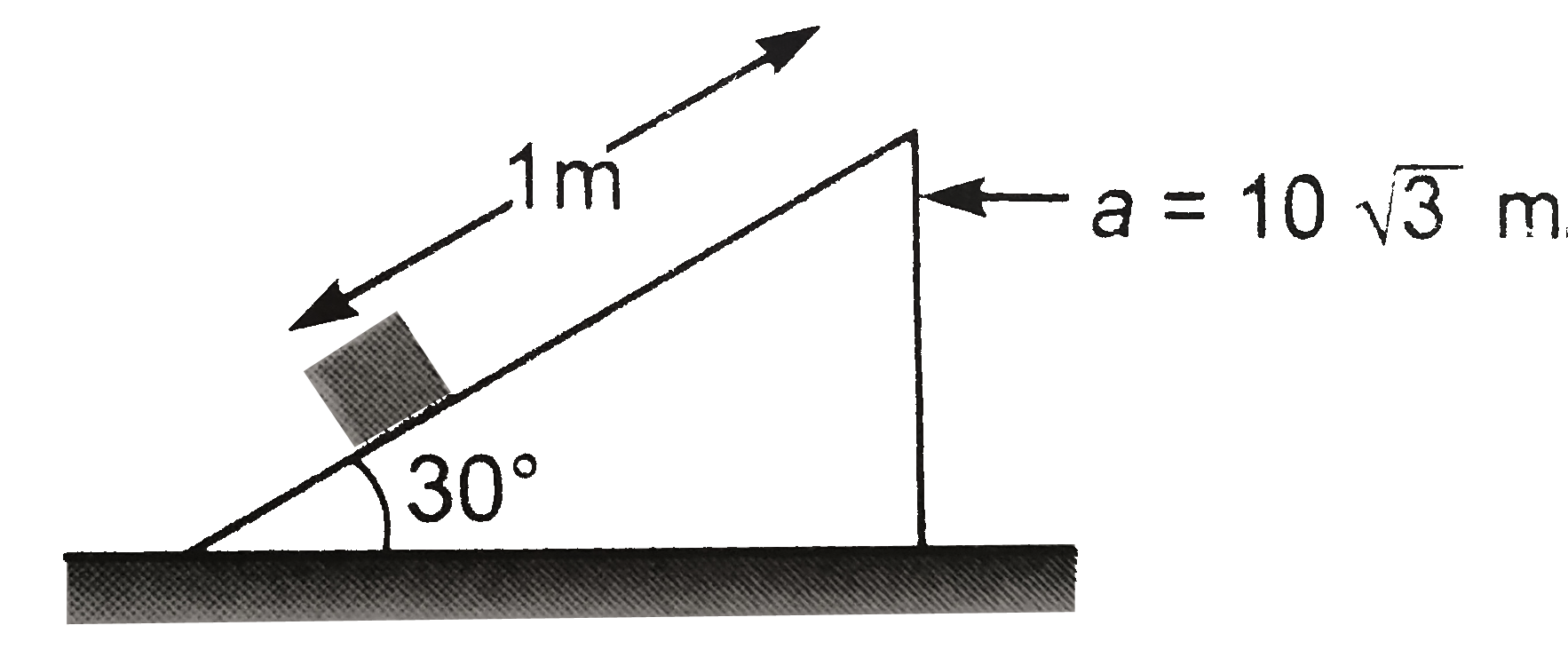
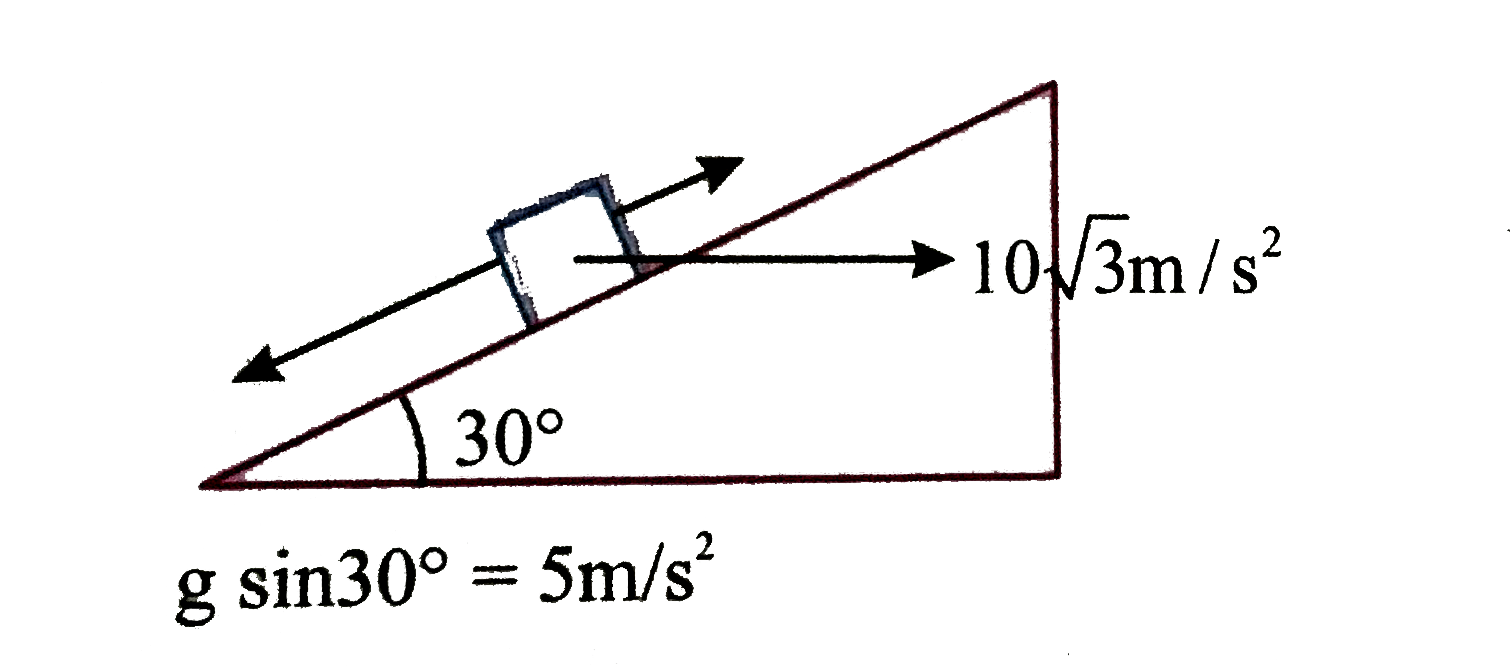
In the figure the wedge is pushed with an acceleration of √3m/s2. It is seen that the block start climbing up on the smooth inclined face of wedge . What will be the time taken by the block to reach the top?
2√5s
1√5s
√5s
√52s
The correct Answer is:B
10√3cos30∘=10√3√32=15m/s2
∴A=15−5=10m/s2∴S=12at2
1=12(10)t2ort=1√5S
 .
.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SINGLE ANSWER QUESTIONS Passage -1
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - INTEGER TYPE QUESTIONS
23 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - NCERT BASED QUESTION
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV
41 Videos
Similar Questions
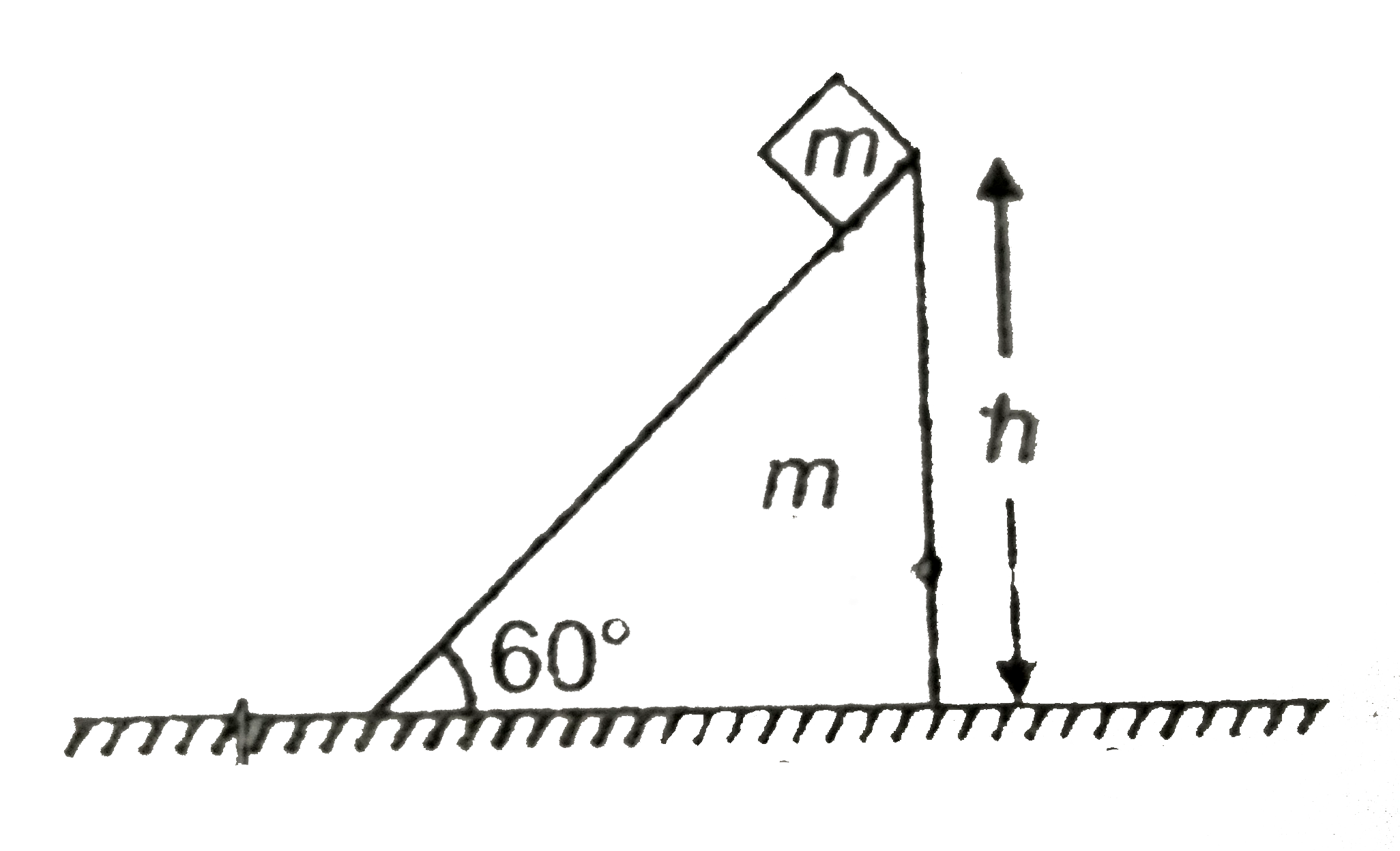
A block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View Solution
Knowledge Check
In the figure the wedge is pushed with an acceleration of √3m/s2. It is seen that the block start climbing up on the smooth inclined face of wedge . What will be the time taken by the block to reach the top?
 A2√5sB√25sC√5sD√52s
A2√5sB√25sC√5sD√52s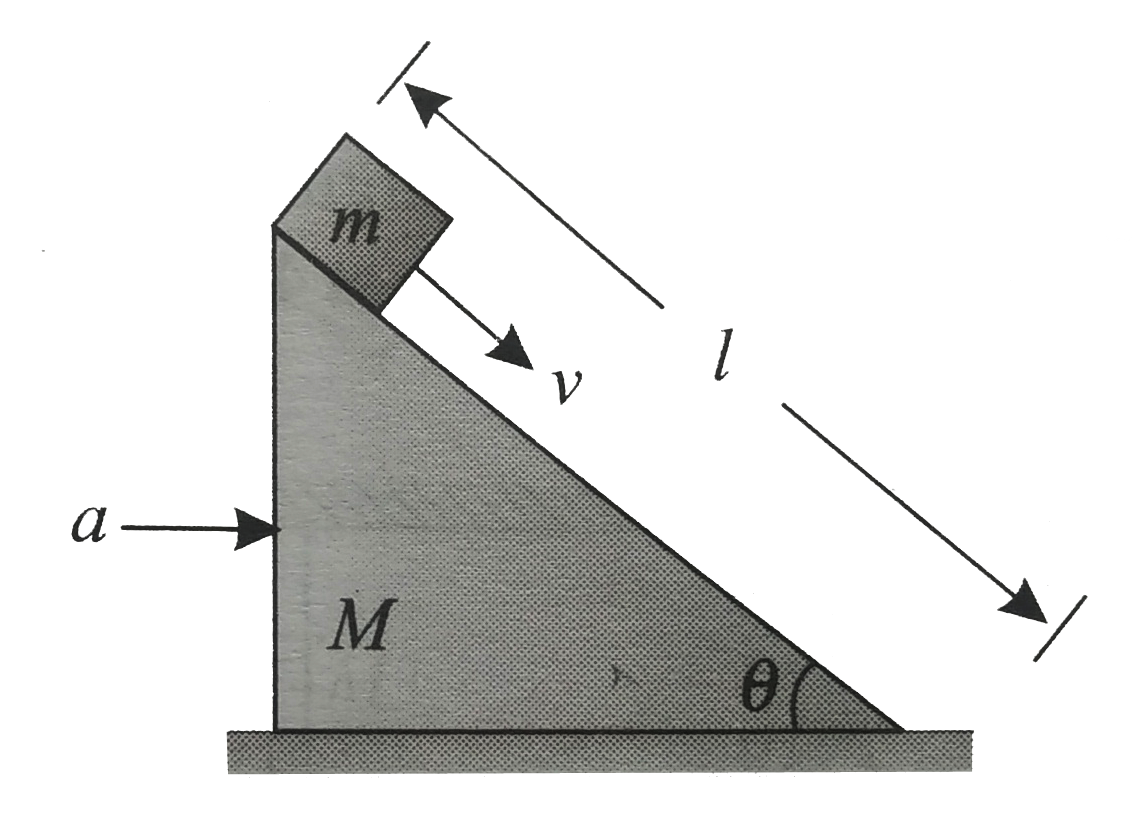
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The time taken by the block to reach the ground is:AlvB√2lgsinθC√2lgcosθDvgsinθA smooth wedge of mass M is pulled towards left with an acceleration a=gcotθ on a horizontal surface and a block of mass m is released w.r.t. wedge. Then answer the following

Time taken by the block to reach the ground isA√2lsinθgB√2lgsinθC√2lgcosθDvgsinθ
A triangular wedge of mass M lies on a smooth horizontal table with half of its base projecting out of the edge of the table. A block of mass m is kept at the top of the smooth incline surface of the wedge and the system is let go. Find the maximum value of Mm for which the block will land on the table. Take θ=60∘.
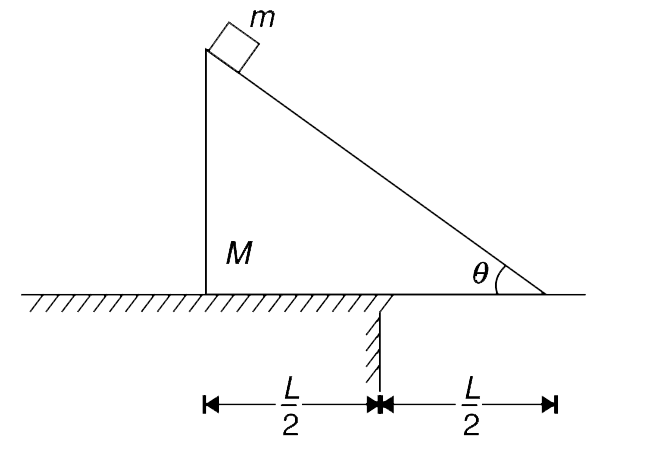
View SolutionA wooden wedge of mass 10m has a smooth groove on its inclined surface. The groove is in shape of quarter of a circle of radius R=0.55m. The inclined face makes an angle θ=cos−1(√115) with the horizontal A block 'A' of mass m is palced at the top of the groove and given a gentle push so as to slide along the groove. There is no friction between the wedge and the horizontal ground on which it has been placed. Neglect width of the groove.
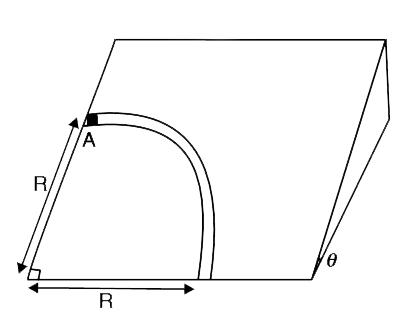
(a) Find the magnitude of displacement of the wedge by the instant the block A reaches the bottom of the groove
(b) Find the velocity of a wedge at the instant the block A reaches the bottom of the groove.
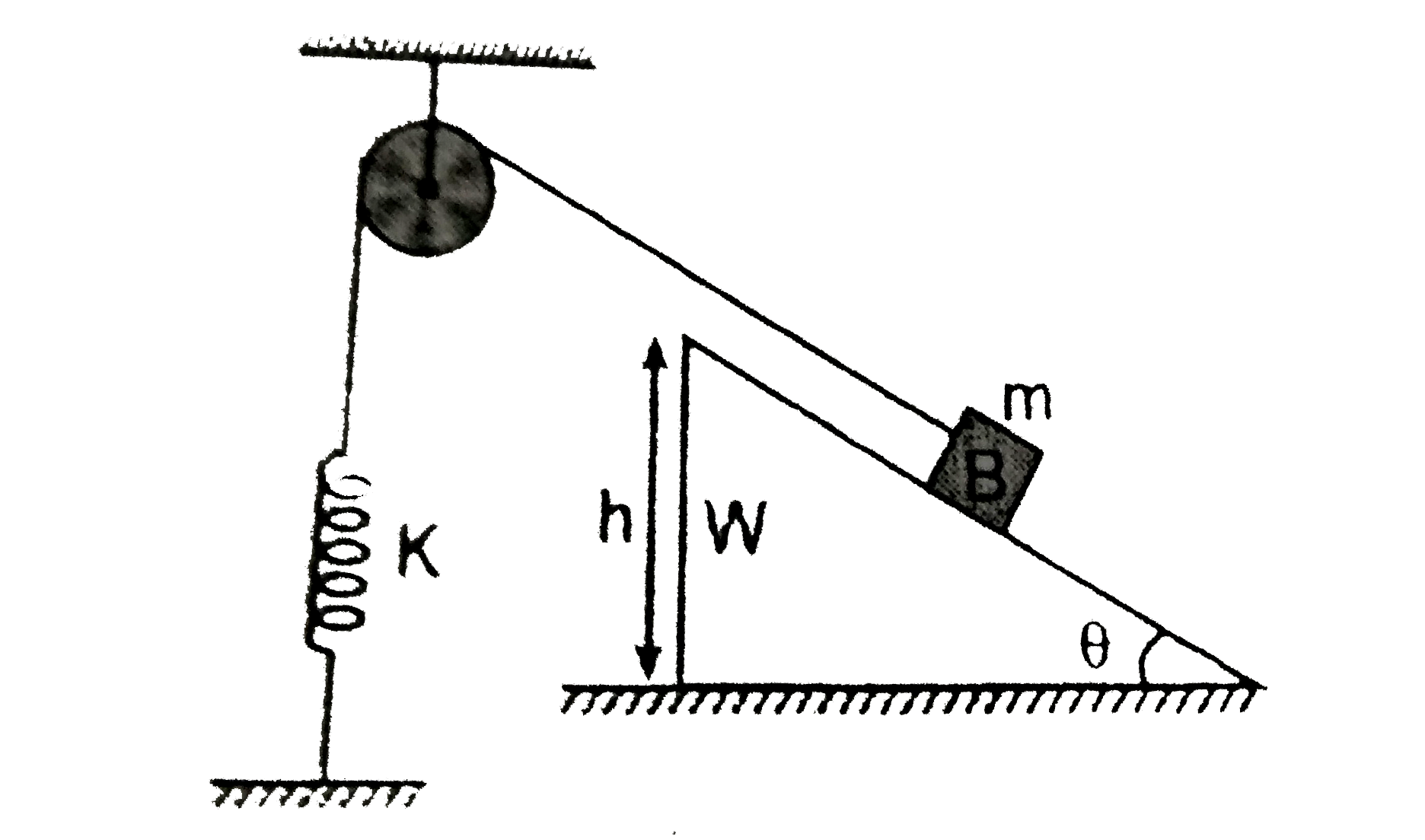
View SolutionIn the figure shown the pulley is smooth . The spring and the string are light. The block 'B' slides down from the top along the fixed rought wedge of inclination θ. Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and the spring was relaxed when the block was relased from the top of the wedge.
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
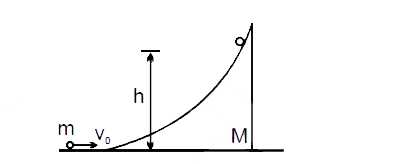
Identify the correct statement(s) related to the situation when the particle starts moving downward
View SolutionFigure shows a block A constrained to slide along the inclined plane of the wedge B shown. Block A is attached with a string which passes through three ideal pulleys and connected to the wedge B. If wedge is pulled toward right with an acceleration a, find
(a) the acceleration of the block with respect to wedge
(b) the acceleration of the block with respect to ground.

View Solution
