The friction coefficient between plank and flooe is μ. The man applies, the maximum possible foce on the string and the system remains at rest. Then

frictional force between plank and surface is 2μmg1+μ
frcitional force on man is zero
tension is the string is 2μmg1+μ
net force on man is zero
The correct Answer is:A, B, C, D
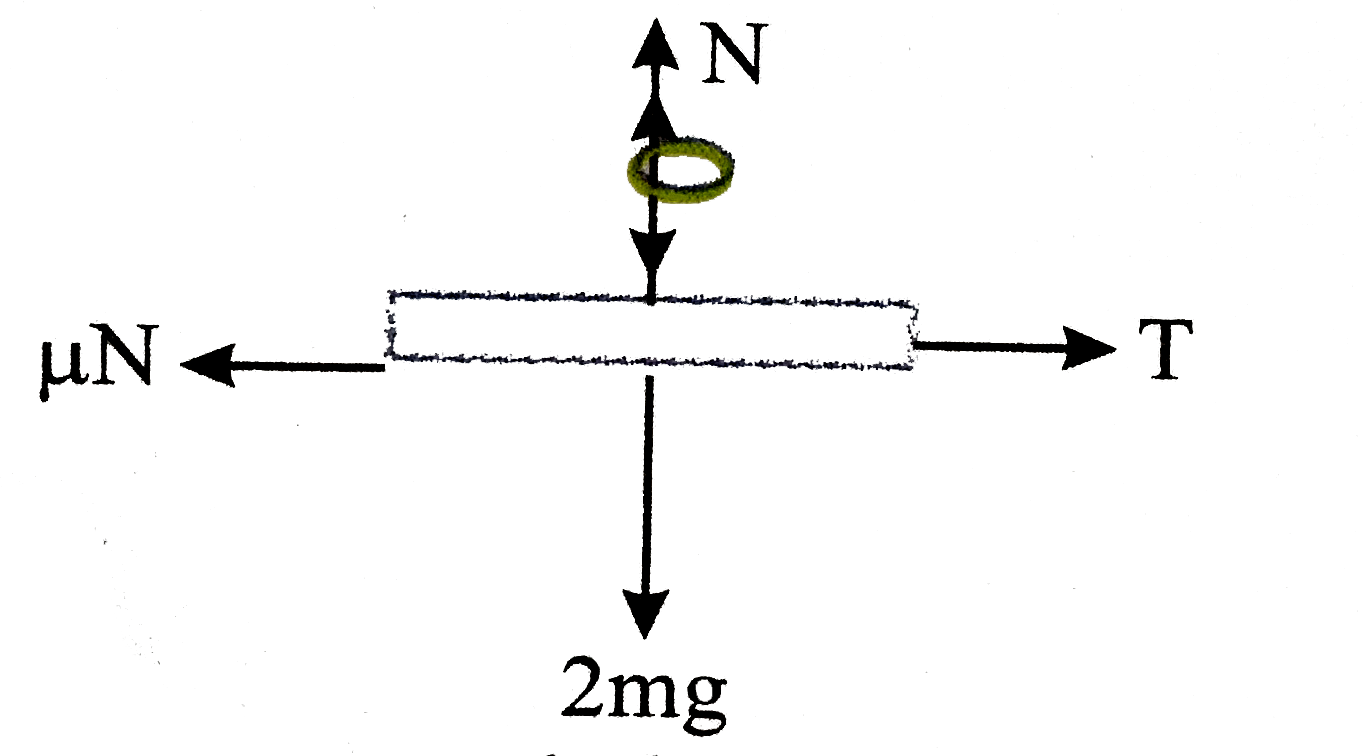
For man and plank as a system
T+N=2mg⇒N=2m−T
T=μN=μ(2mg−T)⇒T=2μmg1+μ,
Friction force −μN=T
No horizontal acts on man, so no friction force will act on man. Also he is in equilibrium so net force acting on man is zero.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions6videos
FRICTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Integer type questions14videos
FRICTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)54videos
COLLISION
- BOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EXERCISE -IV40videos
GRAVITATION
Similar Questions
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor
 View Solution
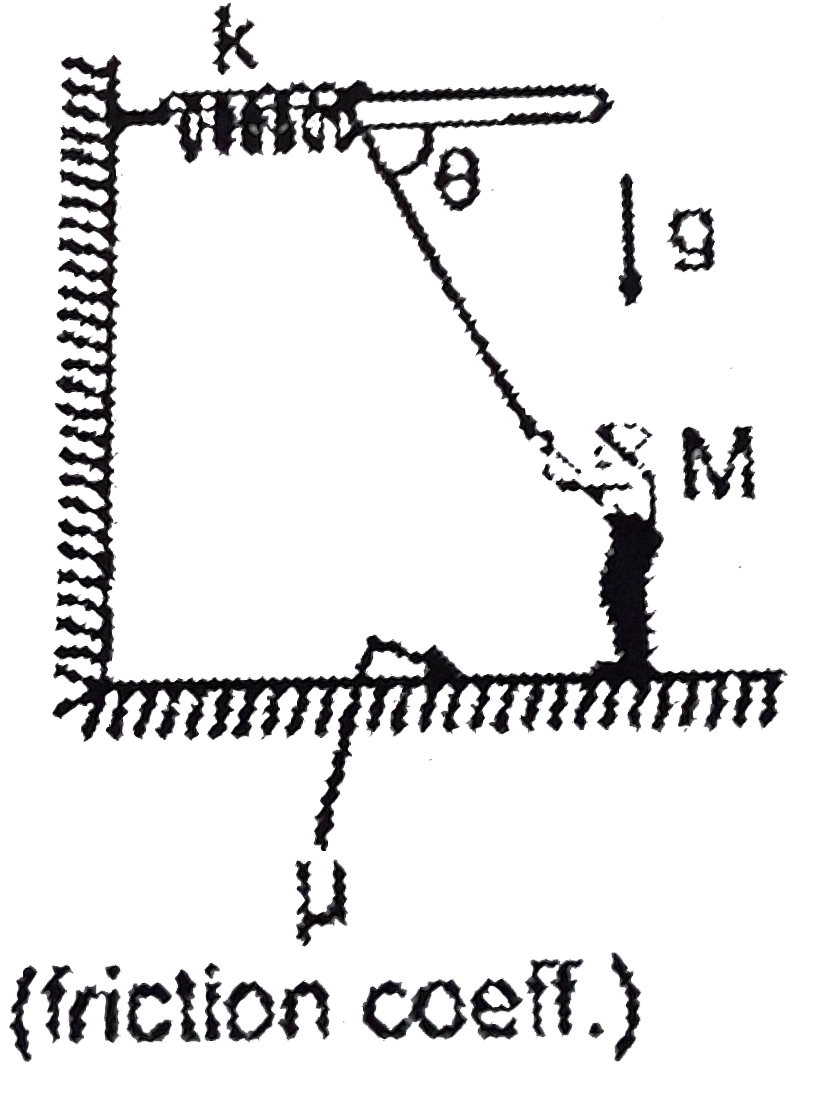
View SolutionA man with mass M has its string'.attached to one end. of a spring which can move without friction along a horizontal, overhead fixed rod. The other end of the spring is fixed to a, wall. The spring constant is k. The string is massless and inextensible and it maintains a constant angle θ with the, overhead rod, even when the man moves. There is friction, iwith coefficient μ between the man and the ground. What is, the maximum distance (in m ) that the man moving slowly can stretch the spring beyond its natural length?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The friction coefficient between the plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then :
 Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zero
Afriction force between plank and surface is 2μmg1+μBfrictional force on man is zeroCtension in the string is 2μmg1+μDnet force on man is zero - Question 2 - Select One
A person throws a ball in vertical plane such that velocity of ball along horizontal is Vx and along vertical is vγ. Coefficinet of friction between man and gound is μ. Necessary condition so that man always remains at rest will be (Note: the process is done in time Δt0)
AVx>μVyBVx≤μVyCVy≤μVxDNone of these - Question 3 - Select One
In the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is μ=0.5 . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.
 A25NB40NC30ND20N
A25NB40NC30ND20N
The friction coefficient between the blocks is μ. If force F is applied on the lower block , analyse motion of two blocks.
 View Solution
View SolutionFigure-2.84 shows a man ofmass M standing on a board of mass m.What minimum force is required to exert on string to slide the board. The friction coefficient between board and floor is μ and there is sufficient friction between man and board so that man does not slip.
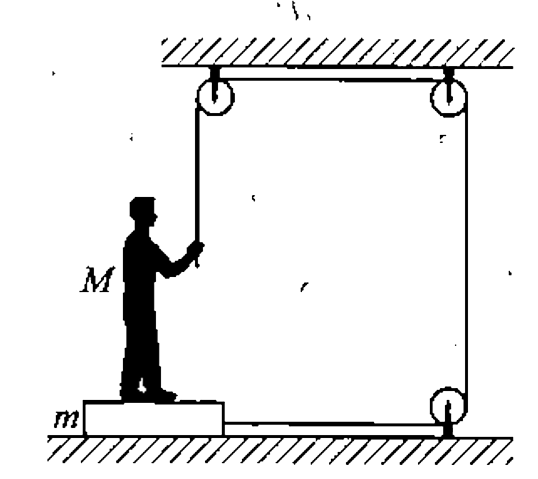
[μ(M+m)g1+μ]View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
 View Solution
View SolutionIn the system shown in Fig the friction coefficient between ground and bigger block is μ There is no friction between both the block .The string connecting both the block is light all three pulley are light and frictionless Then the minimum limiting value of μ so that the system remain in equilibrium , is
 View Solution
View Solution
In the system shown in figure the friction coefficient between ground and bigger block is μ. There is no frinction between both the blocks. The string connecting both the block is light, all three pulleys are light and frictionless. Then the minimum limiting value of μ so that the system remains in equilibrium isView Solution

