A boat of mass 40kg is at rest. A dog of mass 4kg moves in the boat with a velocity of 10m/s. What is the velocity of boat (nearly)?
4m/s
2m/s
8m/s
1m/s
The correct Answer is:D
To solve the problem, we will use the principle of conservation of momentum. The total momentum of the system (boat + dog) before the dog starts moving must equal the total momentum after the dog starts moving.
1. Identify the masses:
- Mass of the boat (M) = 40 kg
- Mass of the dog (m) = 4 kg
2. Initial conditions:
- The boat is initially at rest, so its initial velocity (V_boat_initial) = 0 m/s.
- The dog moves with a velocity (V_dog) = 10 m/s relative to the boat.
3. Final conditions:
- Let the final velocity of the boat be V_boat_final (which we need to find).
4. Apply the conservation of momentum:
- The total initial momentum of the system is:
Pinitial=(M⋅Vboat_initial)+(m⋅Vdog_initial)=(40⋅0)+(4⋅0)=0
- The total final momentum of the system is:
Pfinal=(M⋅Vboat_final)+(m⋅Vdog_final)
- Since the dog moves at 10 m/s relative to the boat, the final velocity of the dog (V_dog_final) can be expressed as:
Vdog_final=Vboat_final+10
5. Set up the equation using conservation of momentum:
0=(M⋅Vboat_final)+(m⋅(Vboat_final+10))
Substituting the values of M and m:
0=(40⋅Vboat_final)+(4⋅(Vboat_final+10))
6. Expand and simplify the equation:
0=40Vboat_final+4Vboat_final+40
0=44Vboat_final+40
7. Solve for V_boat_final:
44Vboat_final=−40
Vboat_final=−4044=−1011≈−0.91 m/s
8. Interpret the result:
The negative sign indicates that the boat moves in the opposite direction to the dog's movement. Thus, the velocity of the boat is approximately 0.91 m/s in the opposite direction.
Final Answer:
The velocity of the boat is approximately 0.91 m/s in the direction opposite to that of the dog's movement.
---
- Mass of the boat (M) = 40 kg
- Mass of the dog (m) = 4 kg
- The boat is initially at rest, so its initial velocity (V_boat_initial) = 0 m/s.
- The dog moves with a velocity (V_dog) = 10 m/s relative to the boat.
- Let the final velocity of the boat be V_boat_final (which we need to find).
- The total initial momentum of the system is:
Pinitial=(M⋅Vboat_initial)+(m⋅Vdog_initial)=(40⋅0)+(4⋅0)=0
- The total final momentum of the system is:
Pfinal=(M⋅Vboat_final)+(m⋅Vdog_final)
- Since the dog moves at 10 m/s relative to the boat, the final velocity of the dog (V_dog_final) can be expressed as:
Vdog_final=Vboat_final+10
0=(M⋅Vboat_final)+(m⋅(Vboat_final+10))
Substituting the values of M and m:
0=(40⋅Vboat_final)+(4⋅(Vboat_final+10))
0=40Vboat_final+4Vboat_final+40
0=44Vboat_final+40
44Vboat_final=−40
Vboat_final=−4044=−1011≈−0.91 m/s
The negative sign indicates that the boat moves in the opposite direction to the dog's movement. Thus, the velocity of the boat is approximately 0.91 m/s in the opposite direction.
The velocity of the boat is approximately 0.91 m/s in the direction opposite to that of the dog's movement.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)64videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-III66videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - C.U.Q.83videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A girl of mass 50 kg jumps out of a rowing boat of mass 300 kg on to the bank, with a horizontal velocity of 3 m/s. With what velocity does the boat begin to move backwards ?
View SolutionA boat of mass 1000 kg is moving with a velocity of 5 m/s. A person of mass 60 kg jumps into the boat. The velocity of the boat with the person will be -
View Solution
Knowledge Check
- Question 1 - Select One
A boat of mass 50kg is at rest. A dog of mass 5kg moves in the boat with a velocity of 20m/s. What is the velocity of boat?
A4m/sB2m/sC8m/sD1m/s - Question 2 - Select One
A person weighing 60kg In a small boat of mass 140kg which is at rest, throws a 5kg stone in the horizontal direction with a velocity of 14m/s−1. The velocity of the boat immediately after the throw is (in m/s)
A1.2B0.5C0.35D0.65 - Question 3 - Select One
A person weighing 60 kg in a small boat of mass 140 kg which is at rest, throws a 5 kg stone in the horizontal direction with a velocity of 14ms−1. The velocity of the boat immediately after the throw is ( in m/s)
A1.2B0.5C0.35D0.65
A ball of mass 1kg moving with a velocity of 15m/s undergoes a head on elastic collision with another ball of unknown mass at rest, and rebound with a velocity of 10m/s. What is the mass of the other ball?
View SolutionA body of mass 1.5kg moving with a velocity of 10m/s encounters another body of mass 2.5kg moving in opposite direction with a velocity of 16m/s, and they stick to eachother. What is the velocity of combination?
View SolutionA person P of mass 50 kg stands at the middle of a boat of mass 100 kg moving at a constant velocity 10 m/s with no friction between water and boat and also the engine of the boat is shut off. With what velocity (relative to the boat surface) should the person move so that the boat comes to rest. Neglect friction between water and boat.
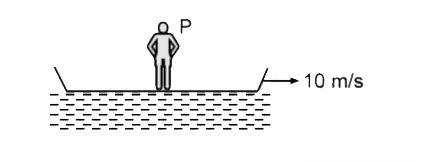 View Solution
View SolutionA bomb of mass 12 kg explodes into two pieces of masses 4 kg and 8 kg. The velocity of mass 4 kg is 20 m/s. Find the velocity of mass 8 kg.
View SolutionA block of mass m in floating in a river flowing with a velocity of 2m/s.A boat is moving behind the block with a velocity of 5m/s with respect to the block as shown.From the boat a stone is thrown with a velocity →v=v1ˆi−vˆj+v3ˆk with respect to the river such that it hits the block.If v1:v2:v3=2√3:2:3 then the velocity of the stone with respect to the ground is (g=10m/s2)
 View Solution
View Solution

