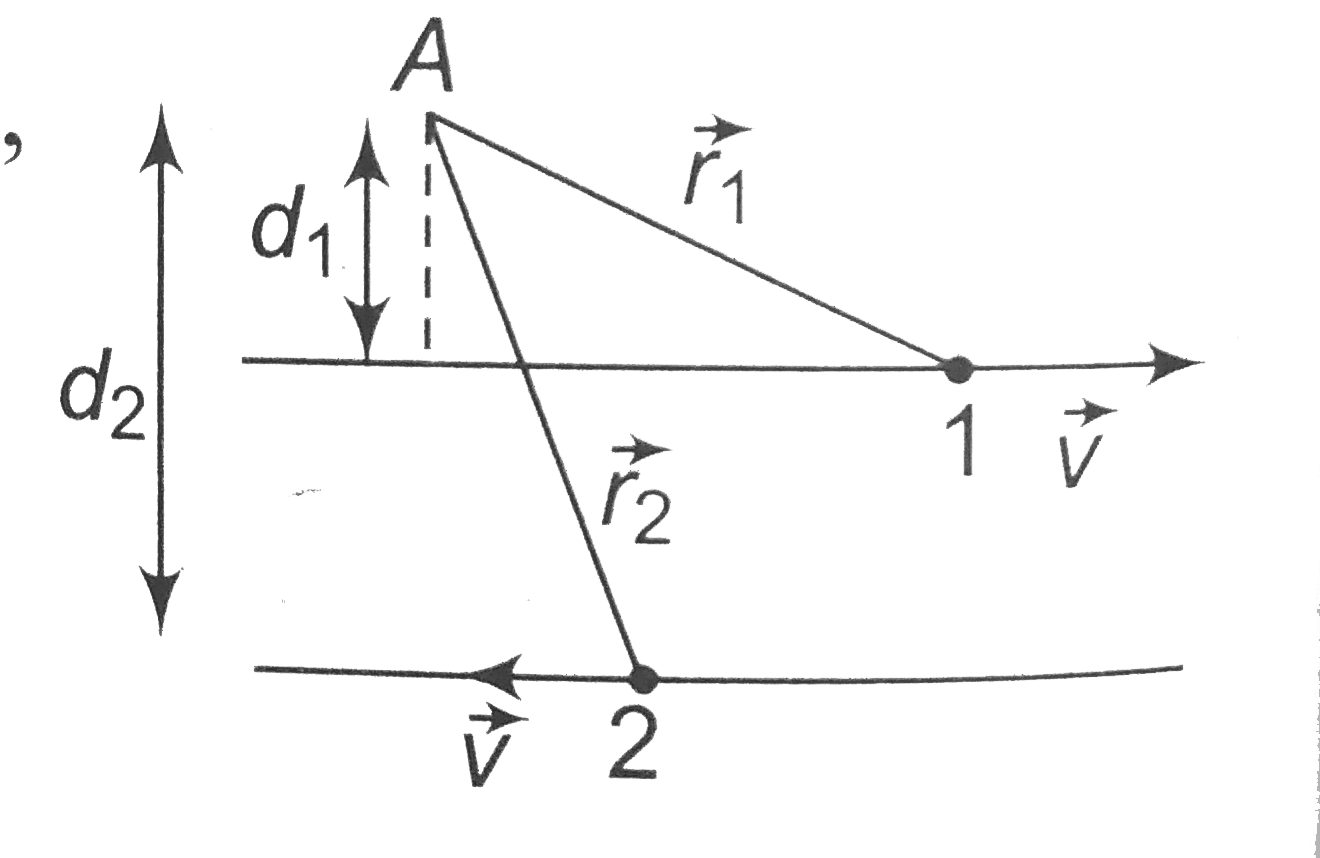
Figure shows two identical particles $1$ and $2$ , each of mass $m$ , moving in opposite directions with same speed $\to V$ along parallel lines. At a particular instant, ${\to r}_{1}$ and ${\to r}_{2}$ are their respective position vectors drawn from point $A$ which is in the plane of the parallel lines. Which of the following is the correct statement ?
.

Angular momentum $l_{1}$ of particle $1$ about $A$ is $l_{1} = m v d_{1} ⊙$

Angular momentum $l_{2}$ of particle $2$ about $I$ is $l_{2} = m v r_{2} ⊙$

Total angular momentum of the system about $A$ is $l = m v (r_{1} + r_{2}) ⊙$

Total angular momentum of the system about $Z$ is $l = m v (d_{1} - d_{2}) \otimes$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Let $\to a and \to b$ be the position vectors of A and B respectively. If C is the point $3 \to a - 2 \to b$ , then which one of the following is correct?
AA. C is in between A and B
BB. A is in between C and B
CC. B is in between A and C
DD. A, B and C are not collinear
Let $\to a and \to b$ be the position vectors of A and B respectively. If C is the point $3 \to a - 2 \to b$ , then which one of the following is correct?
AC is in between A and B
BA is in between C and B
CB is in between A and C
DA, B, C are not collinear
Let $\to v_{1}, \to v_{2}, \to v_{3}, \to v_{4}$ be unit vectors in the xy-plane, one each in the interior of the four quadrants. Which of the following statements is necessarily ture. ?
A $\to v_{1} + \to v_{2} + \to v_{3} + \to v_{4} = 0$
BThere exist i, j with $1 \leq i < j \leq 4$ such $\to v_{i} + \to v_{j}$ is in the first quadrant
CThere exits i, j with $1 \leq i < j \leq 4$ such that $\to v_{i} \cdot \to v_{j} < 0$
DThere exits i, j with $1 \leq i < j \leq 4$ such that $\to v_{i} \cdot \to v_{j} > 0$