A Merry -go-round, made of a ring-like plarfrom of radius , is revolving with angular speed . A person of mass is standing on it. At one instant, the person jumps off the round, radially awaay from the centre of the round (as see from the round). The speed of the round after wards is
The correct Answer is:A
Aa no external torque acts on the system, angular moemtum should be conserved. Hence, ....(i)
Where is moment of inertia of the system and is angular velocity of the system
From eq. (i)
(where and are angular velocities before and after jumping)
(as mass reduce to half, hence, moment of inertia also reduced to half)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -I(H.W)58videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-III66videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionA satellite of mass m is in a circular orbit of radius r round the Earth. Calculate its angular momentum with respect to the centre of the orbit in terms of the mass M of the Earth and G.
View Solution
Knowledge Check
- Question 1 - Select One
A merry-go-round, made of ring-like platform of radius R and mass M is revolving with angular speed ω. A person of mass M is standing on it. At one instant, the person jumps off the round, radially away from the centre of the round (as seen from the round). The speed of the round of afterward is ............
A2ωBωCω2D0 - Question 2 - Select One
A merry -go-round , made of a ring-like platform of radius R and mass M, is revolving with angular speed ω . A person of mass M is standing on it . At one instant , the person jumps off the round , radially away from the centre of the round . The speed of the round afterwards is
A2ωBωCω2D0 - Question 3 - Select One
A girl of mass M stands on the rim of a frictionless merry-go-round of radius R and rotational inertia I that is not moving. She throws a rock of mass m horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the rock. relative to the ground, is v. After, the linear speed of the girl is.
 .AmvR2I+MR2B(m+M)vR2I+MR2CmvR2I+(M+m)R2DmvR2I+(M−m)R2
.AmvR2I+MR2B(m+M)vR2I+MR2CmvR2I+(M+m)R2DmvR2I+(M−m)R2
A uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
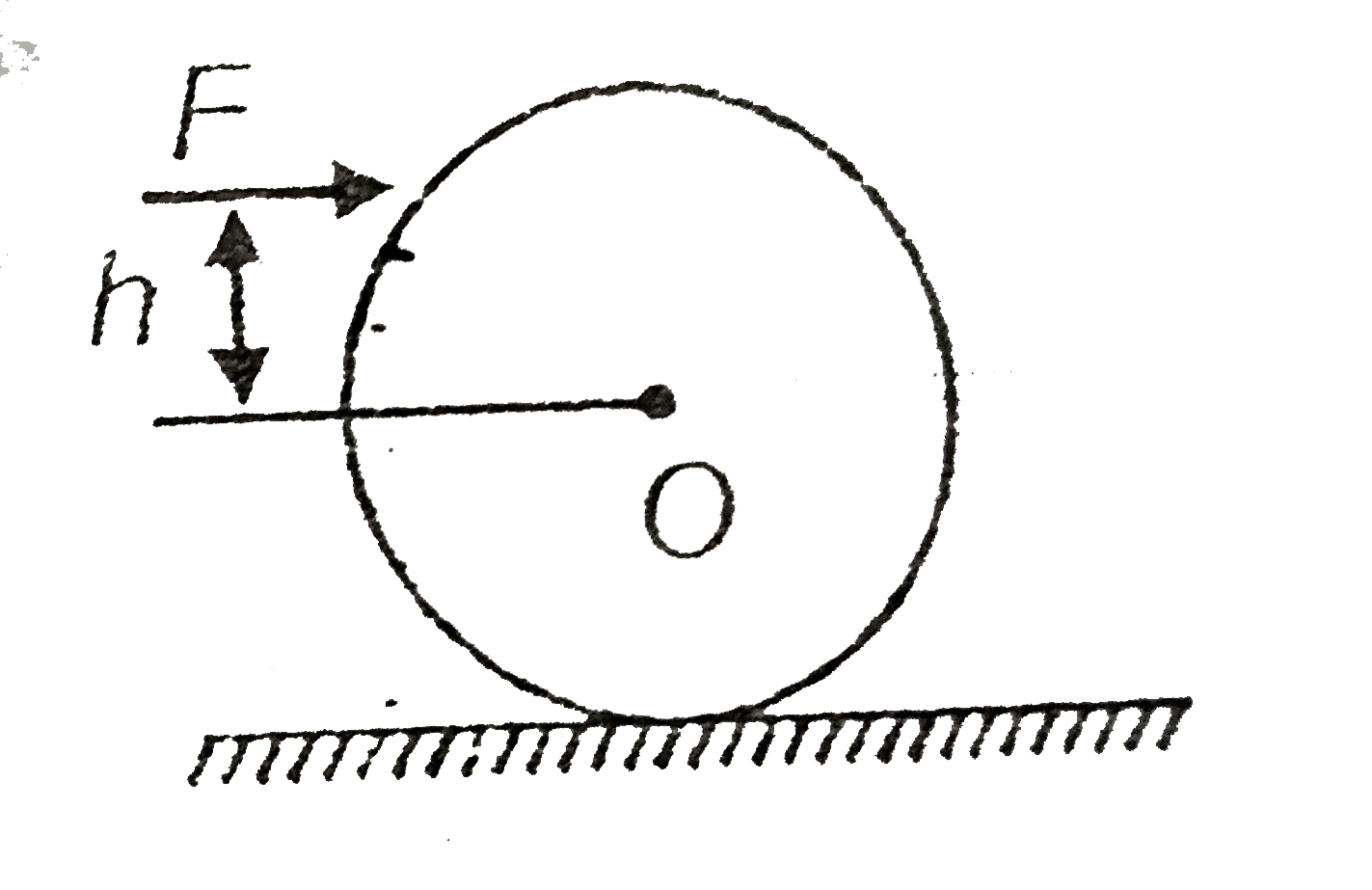 View Solution
View SolutionA scooter is going round a circular road of radius 100 m at a speed of 10m/s . The angular speed of the scooter will be
View SolutionA child is standing on the edge of a merry-go-round that has the shape of a disk, as shown in the figure. The mass of the child is 40 kg. The merry-go-round has a mass of 200kg and a radius of 2.5 m, and it is rotating with an angular velocity of ω=2.0 radians per second. The child then walks slowly towards the centre of the merry-go-round. What will be the final angular velocity of the merry-go-round when the child reaches the centre? (The size of the child can be neglected)
 View Solution
View SolutionA merry -go-round - is moving at a non - varying speed of 10 m/s . It implies that
View SolutionA cord is wound round the circumference of a solid cylinder radius R and mass M. The axis of the cylinder is horizontal. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h.

If the mass starts from rest and falls a distance h, then its speed at that instant is:View Solution

