A circular wooden hoop of mass $m$ and radius $R$ rests fiat on a frictionless surface. A bullet, also of mass $m$ and moving with a velocity $v$ , strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than $R$ . Find the angular velocity with which the system rotates in after the bullet strikes the hoop.

A

$\frac{υ_{0}}{2 R}$

B

$\frac{3 υ_{0}}{R}$

C

$\frac{υ_{0}}{3 R}$

D

$\frac{3 υ_{0}}{R}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Let velocity of $C M$ of hoop be $V_{1}$ and angular velocity of hoop be $ω$ , resultant velocity of bullet just after so collision is $V_{1} + R ω$
From conservation of momentum, we get
$M υ_{0} = m V_{1} + m (V_{1} + ω R) ... (1)$

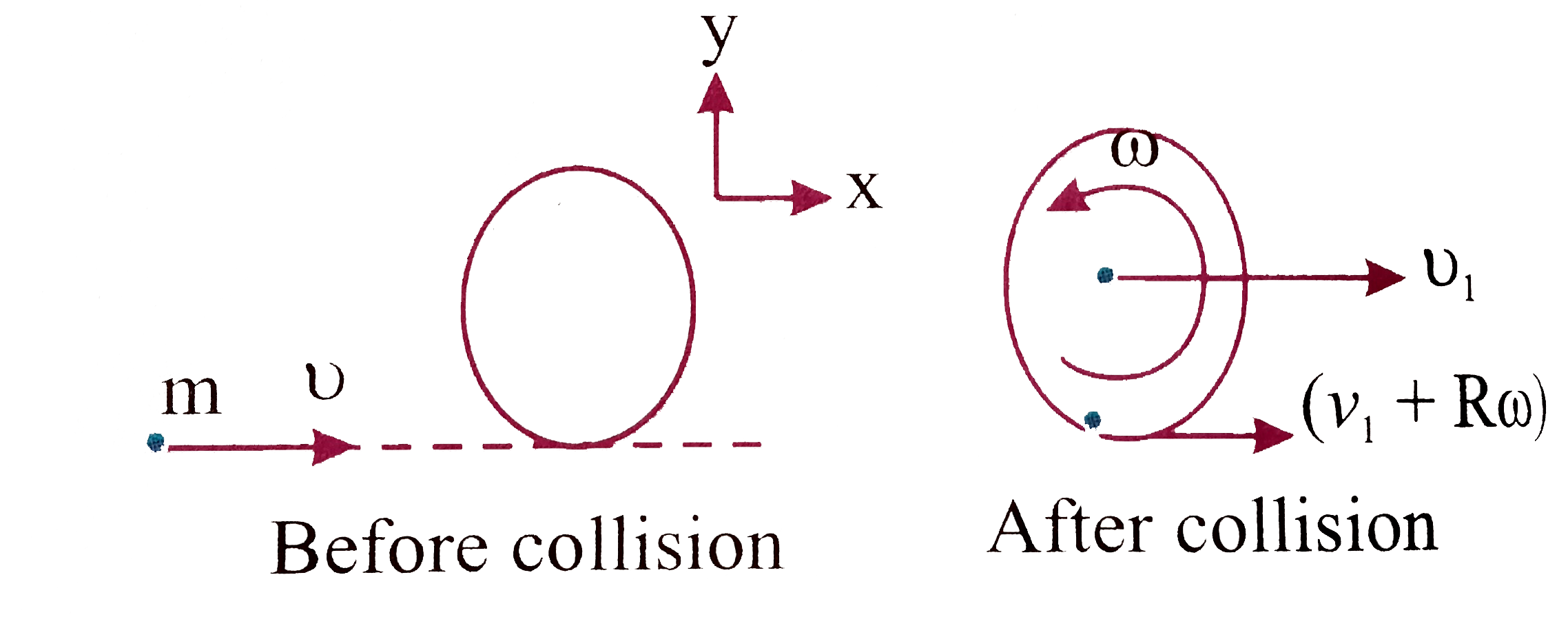
From conservation of angular momentum about $O$ ,
Which is a point on ground just below the point of impact
$L_{i} = 0$
$L_{f} = - m V_{1} R + m R^{2} ω$
$L_{i} = L_{f}$
$V_{1} = R_{ω}$
from eqns (1) and (2), we get
$ω = \frac{υ_{0}}{3 R}$ and $V_{1} = \frac{υ_{0}}{3}$
Absolute velocity of bullet $= V_{1} + R ω = \frac{2 υ_{0}}{3}$
Impulse on bullet
$= 4 \to P = \frac{2 m υ_{0}}{3} ˆ i - m υ_{0} ˆ i = - \frac{m υ_{0}}{3} i$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circular hoop of mass m and radius R rests flat on a horizontal frictionless surface A bullet also of mass m and moving with a velocity v strikes the hoop and gets embedded in it the thickness of the hoop is much smaller then R the angular velocity with which the system rotates after the bullet strikes the hoop is

A $V / (4 R)$
B $V / (3 R)$
C $2 V / (3 R)$
D $3 V / (4 R)$
Question 2 - Select One
A circular hoop of mass $m$ and radius $R$ rests flat on a horizontal smooth surface. A bullet of same mass $m$ and moving with velocity $υ$ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Mark the correct option
Aenergy of system (hoop+ bullet) is conserved
Bmomentum of system is conserved
Cangular momentum of system is conserved about any point in the plane of hoop
Dangular momentum is not conserved due to torque of gravitational force.
Question 3 - Select One
A circular hoop of mass $m$ and radius $R$ rests flat on a horizontal smooth surface. A bullet of same mass $m$ and moving with velocity $υ$ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

What is the impulse on bullet?
A $\frac{- 2 μ ψ l o n_{0}}{3} ˆ i$
B $\frac{- μ ψ l o n_{0}}{3} ˆ i$
C $m υ_{0} ˆ i$
D $\frac{m υ_{0}}{2} ˆ i$

NARAYNA-SYSTEM OF PARTICLES-Level-V

Home
Ask Doubt
Profile