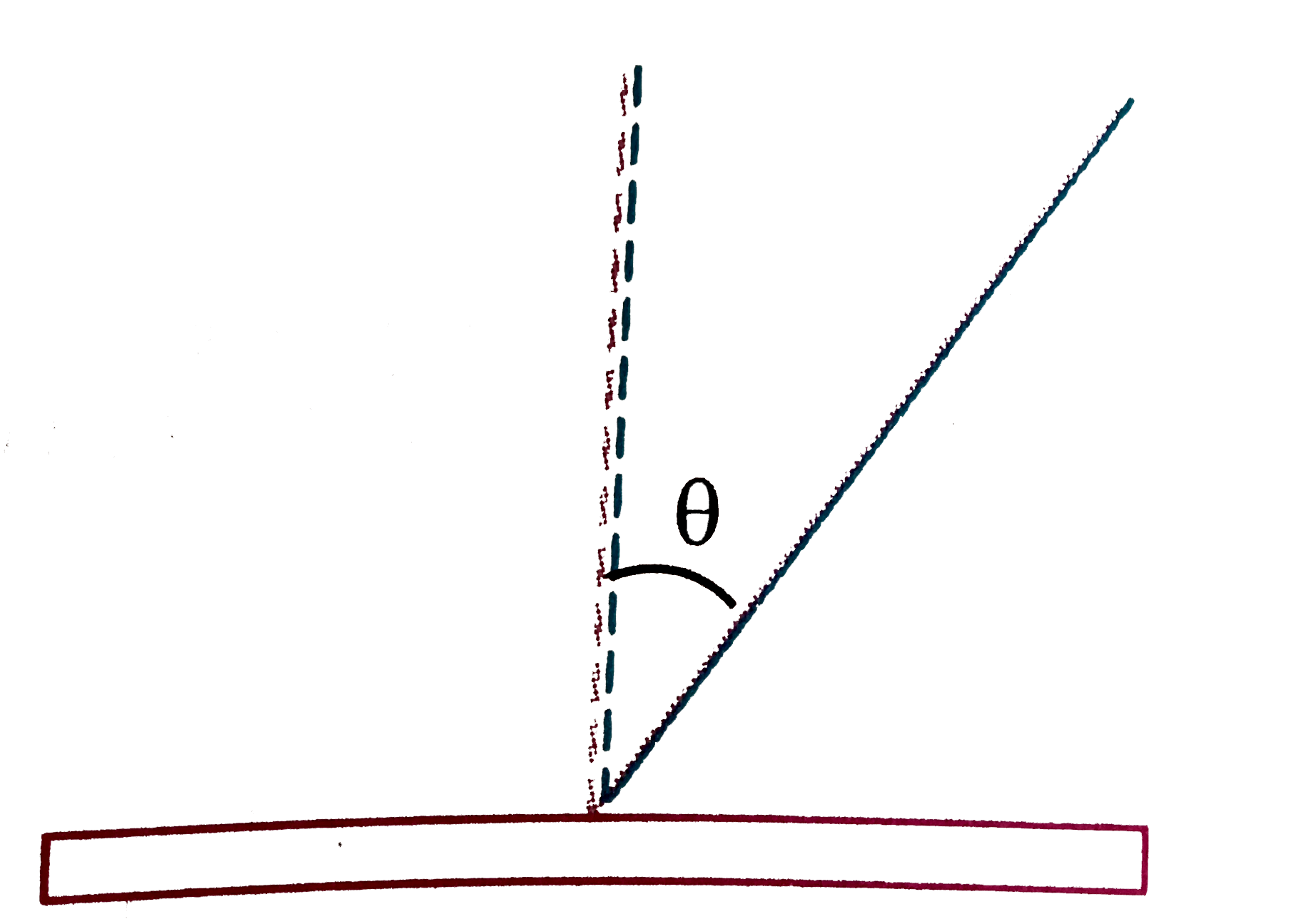
A rod of mass m and length l is released from rest from vertical position as shown in the figure. The normal force as a function of θ, which is exerted on the rod by the ground as it falls downwards, assuming that it does not slip is mg(3cosθ−1n)2 then n=
The correct Answer is:2
At angle θ
12Iω2=mgl2(1−cosθ)or, ω2=3gl(1−cosθ)...(i)
Differentiating w.r.t q.,
α=mgl2sinθml23=32gsinθl.....(ii)
an=l2ω2=3g2(1−cosθ) and at=l2α=34gsinθ
f=max=m(atcosθ−ansinθ)
=m(34gsinθcosθ−3gsinθ2(1−cosθ))
=32mgsinθ[32cosθ−1]
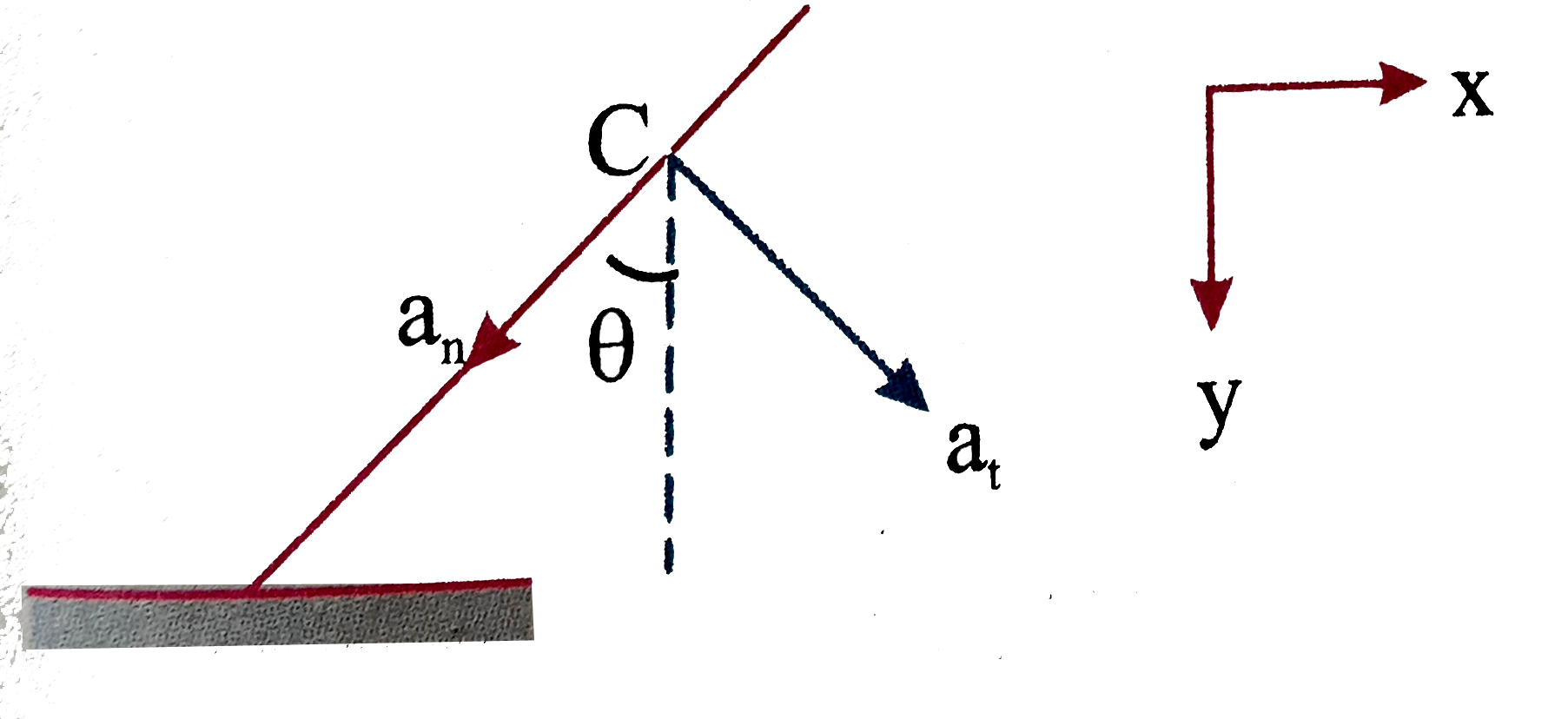
Further, mg−N=mayor,
N=m(g−at)
N=m[g−34gsin2−3gcosθ2(1−cosθ)]
=mg4[4−3sin2θ−6cosθ+6cos2θ]
=mg2(1−3cosθ)2
. The rod does not slip until N=0
i.e.,
θ=cos−1(13)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png) View Solution
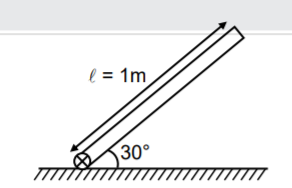
View SolutionA rod of length 1 m is released from rest as shown in the figure below: If ω of rod is √n at the moment it hits the ground, then find n.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14 - Question 2 - Select One
One end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mg - Question 3 - Select One
One end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mg
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
 View Solution
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 View Solution
View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is
 View Solution
View Solution

