A thin uniformed rod of mass m and length L is hinged at one end and from other end a light string is attached. The string is wound over a frictionless pullely (having mass 2m) and a block of mass 2m is connected to string on other side of pulley as shown. the system is released from rest when the rod id making an angle of 37∘ with horizontal. Based on above information answer the following question :
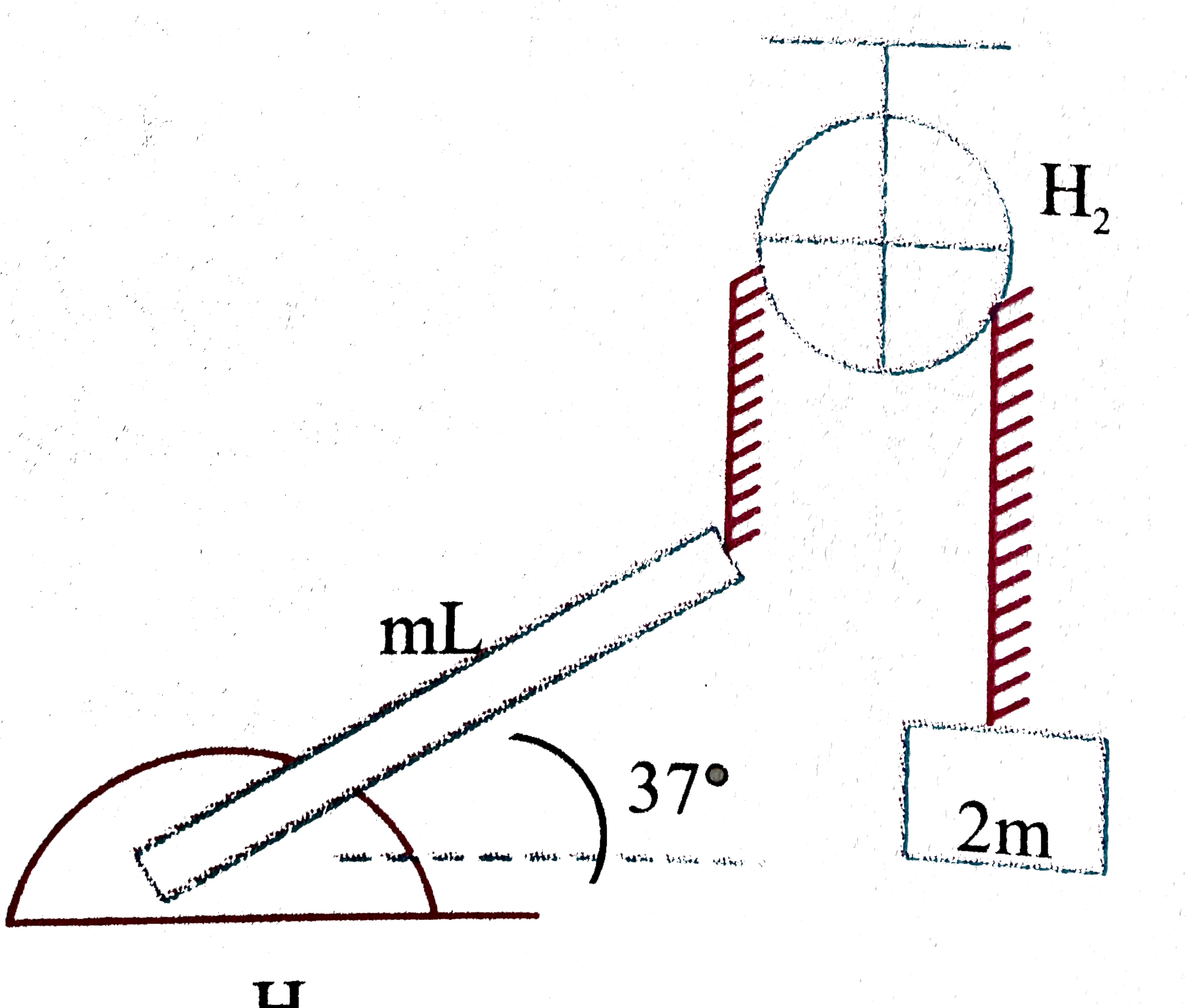
Just after releases of the system from rest acceleration of block is
72g121, downwards
48g119, downwards
90g121, downwards
90g121,upwards
The correct Answer is:A

Let α be the angular acceleration of rod about hinge and a be the acceleration of block just after the system is released from rest.
The free body diagram of rod, pulley and block are shown in figure. in free body diagram of rod, the forece exerted by hinge on rod is not shown. For rod, mg×L2cos37∘−T×Lcos37∘
=−Iα[I=mL23]
For block, 2mg−T=2ma
From constraint, a=Iαcos37∘=4Lα5
Solving above equations, we get
a=72g121,α=90g121L,T=98mg121
Reactions force exerted by H2 on pulley
is, N1=2T+2mg=438121mg
Now draw the complete fee body diagram of rod as follows
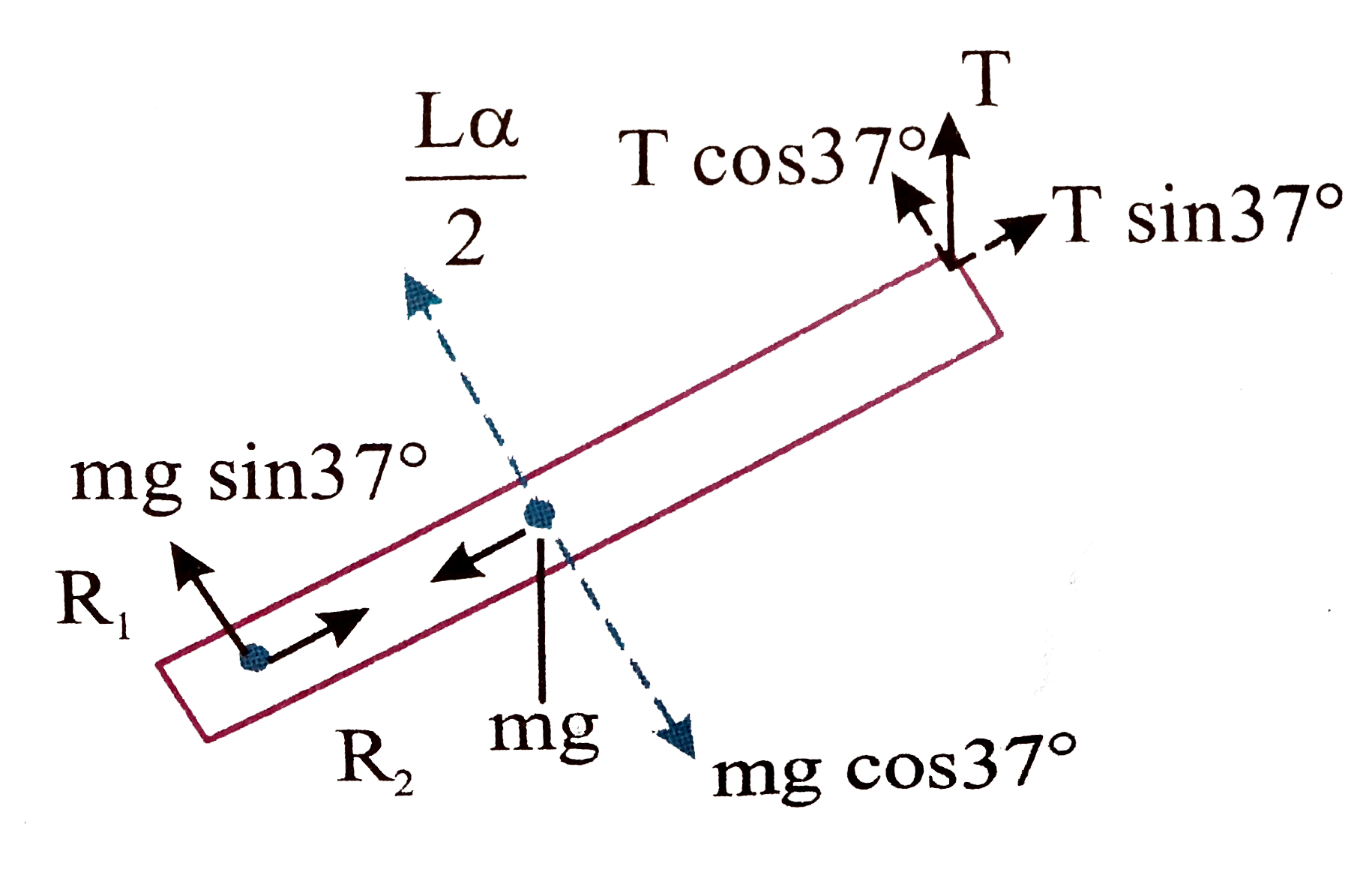
⇒R1+Tcos37∘−mgcos37∘=mL2α
⇒R2+Tsin37∘=mgsin37∘
Net reactions force on rod due to hinge is,
F=√R21+R22
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
The point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
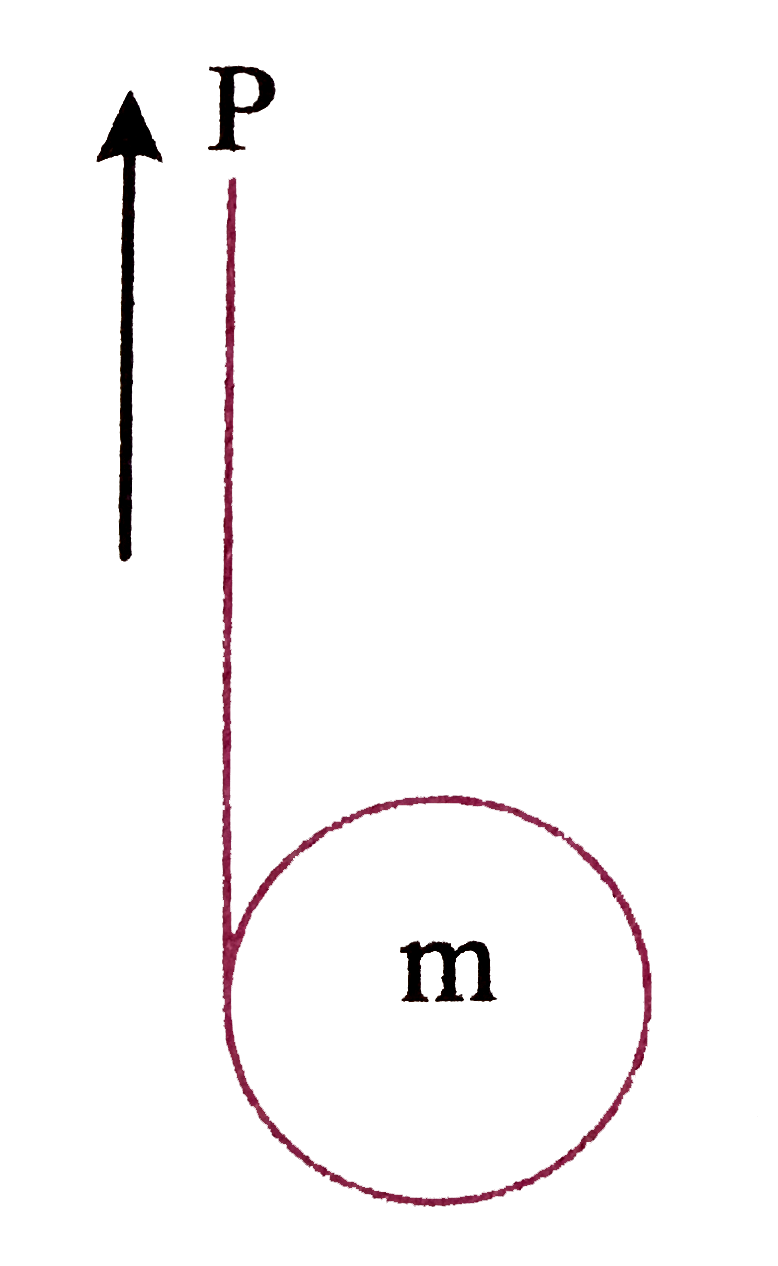 05:14View Solution
05:14View SolutionFour particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
07:47View SolutionWhat is the discovery of CV Raman?
View SolutionFor which of the following does the centre of mass lie outside the body ?
02:55View SolutionUniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to m Then acceleration of block just after release from this position is
05:16View SolutionA ring of mass m=1kg can slide over a smooth vertical rod. A light string attached to the ring passing over a smooth fixed pulley at a distance of L=0.7m from the rod as shown in figure. At the other end of the string mass M=5kg is attached, lying over a smooth fixed inclined plane of inclination angle 37^@ . The ring is held in level with the pulley and released. Determine the velocity of ring when the string makes an angle (alpha=37^@) with the horizontal. [sin 37^@=0.6]
01:26View SolutionA block of mass 2m is attached to a string of length L=5m. The block is released when the string is horizontal , it picks up a particle of 2m kept at rest at the lowest point. The maximum height attached by the combined mass is
View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :
 02:45View Solution
02:45View SolutionUniform rod AB is hinged at end A in horizontal position as shown in the figure the other end is connected to a block through a massless string m as shown the pulley is smooth and massless masses of block and rod is same and is equal to m then acceleration of block just after release from this position is
 02:45View Solution
02:45View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :
 04:41View Solution
04:41View SolutionUniform rod Ab is hinged at the end A in the figure. The other end of the rod is connected toa block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are
 View Solution
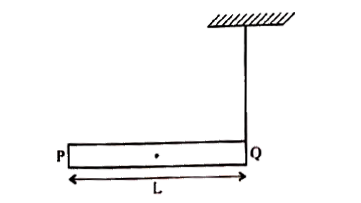
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a mass less than string tied at a point Q as shown in figure. When string is cut, the initial acceleration rod is:
 View Solution
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a mass less than string tied at a point Q as shown in figure. When string is cut, the initial acceleration rod is:
06:12View SolutionTwo masses, m and 2m are connected by a string that passes over a frictionless pulley. When the mass 2m is released, acceleration of the mass m upwards, will be
08:36View SolutionTwo masses (M+m)and(M−m) are attached to the ends of a light inextensible string and the string is made to pass over the surface of a smooth fixed pulley. When the masses are released from rest, the acceleration of the system is
04:43View Solution

