A rough disc of mass m rotates freely with an angular velocity ω. If another rough disc of mass m2 and same radius but spinning in opposite sense with angular speed ω is kept on the first disc. Then:
the final angular speed of the dise is ω3
the net work does by friction is zero
the friction does a positive work on the lighter disc
the net work done by friction is −mR2ω23
The correct Answer is:A, D
12mr2×ω−12m2r2×ω=(12mr2+14mr2)ω'
⇒ω'=ω/3
d) use work energy principle
wf+wg=Δ(DE)⇒12(34mr2)ω2/9
−[14mr2ω2+18mr2ω2]
⇒wf+0=−mω2r23
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V
72 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity ω. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
View Solution
Knowledge Check
A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertiaA disc rotates with angular velocity ω and kinetic energy E. Then its angular momentum
AIωBL=EωCL=2EωDL=ωEA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
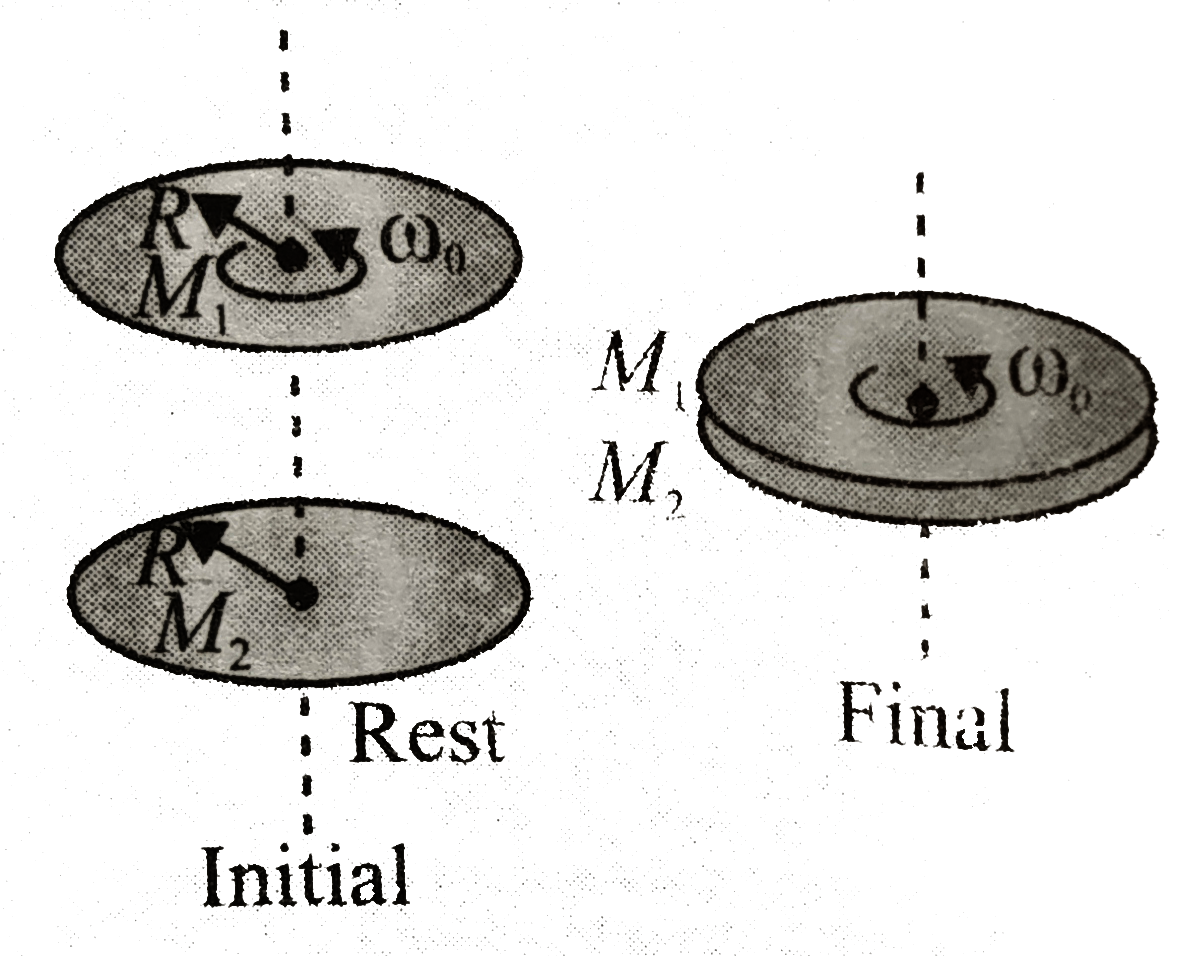 Am1m2Bm2m1+m2Cm2m1Dm1m1+m2
Am1m2Bm2m1+m2Cm2m1Dm1m1+m2
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same thickness and radius but mass 18M is placed gently on the first disc co-axially. The angular velocity of the system is now
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to the plane at an angular velocity ω . Another disc of mass M / 3 but same radius is placed gently on the first disc coaxially . the angular velocity of the system now is
View SolutionA uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
View SolutionA thin and circular disc of mass m and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . If another disc of same dimension but mass ml4 is placed gently on the first disc co-axially, then the new angular velocity of the system is
View SolutionA circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
View Solution
