The KE and moment of inertia about the given end point of a rod of mass m and length l and cross sectional area A which is rotating with ω=√gl as shown in figure. Will be [density of the rod varies as ρ=ρ0(1+xl),x is the distance measured from O)n ]
![The KE and moment of inertia about the given end point of a rod of mass m and length l and cross sectional area A which is rotating with omega=sqrt(g/l) as shown in figure. Will be [density of the rod varies as rho=rho(0)(1+x/l),x is the distance measured from O)n ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NAR_PHY_XI_V03_C01_E01_507_Q01.png)
KE=736mgl
I=7ρ0Al336
KE=739mgl
I=11ρ0Al336
The correct Answer is:A, B
I=∫L013dmx2
=∫l013ρ0(1+xl)(Adx)x2=13ρ0A∫l0[x2dx+x3ldx]
=13ρ0A[l33+1l×l44]=7ρ0Al336
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Moment of inertia of a thin rod of mass 'M' and length 'L' perpendicular to rod at mid point is
AMl22,BMl23CMl212DNone of these - Question 2 - Select One
A uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod isA3FL8AYB3FL5AYC8FL3AYD5FL3AY - Question 3 - Select One
Find the M.I. of thin uniform rod of mass M and length L about the axis as shown.
 A
A B
B C
C D
D
Calculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
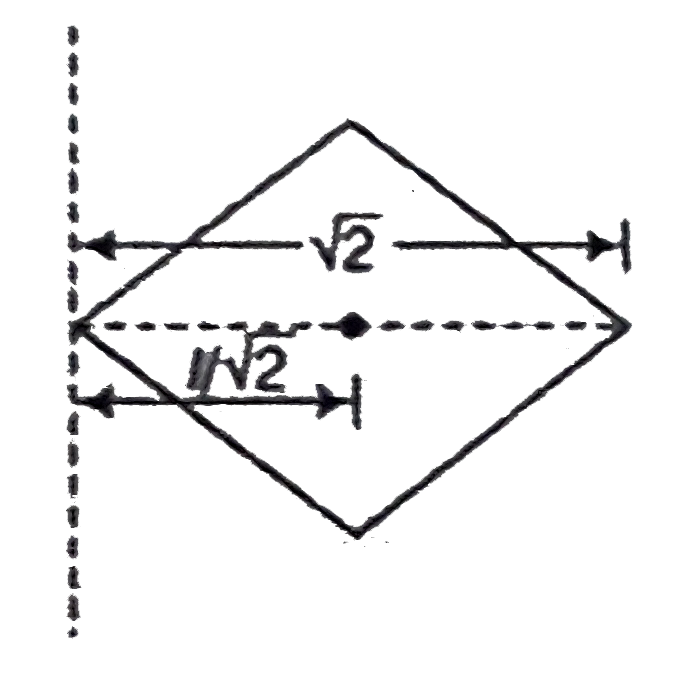
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
 View Solution
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionA uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View Solution

