A rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find
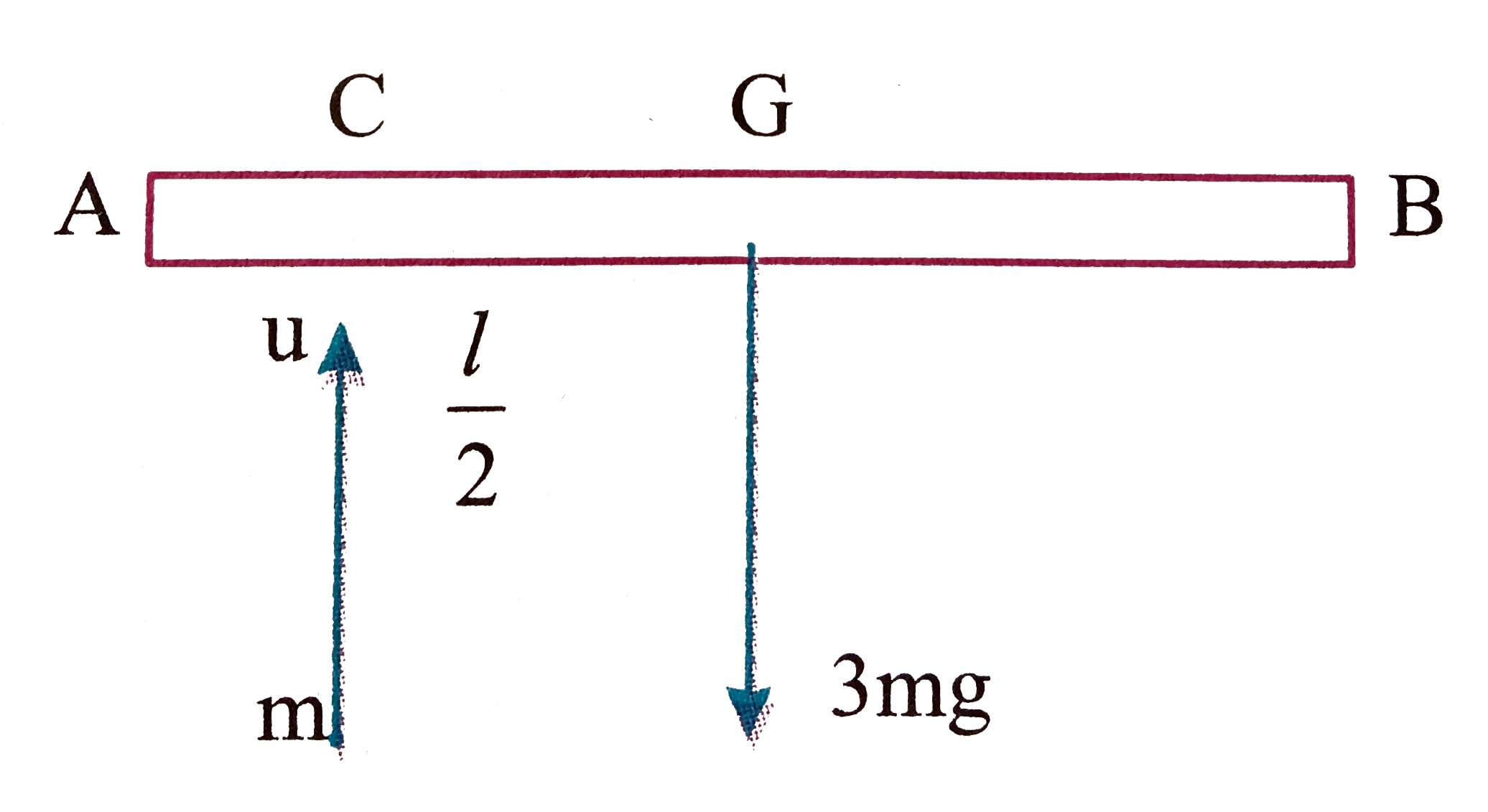
The speed of B immediately after the impact is
1927udown
1927uup
2719udown
2719uup
The correct Answer is:C
In order to use the law of restitution. We need the speed of point C, which is u1−aω (down wards)
law of restitution now given relative velocity of separation at point of impact =e(relative velcity of approch) or u2−(u1−aω)=e(u+u)
hence 2u=u2−u1+aω
For the rod the speed of the particle is 2919υ (down wards)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View SolutionA uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.View Solution
Knowledge Check
- Question 1 - Select One
A rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find

The velocity of the particle immediately after the impactA2919udownB1929udownC2919,uupD2719udown - Question 2 - Select One
A rod AB of mass 3m and length 4a is falling freely in a horizontal position and c is a point distance a from A. When the speed of the rod is u, the point c collides with a particle of mass m which is moving vertically upwards with speed u. if the impact between the particle and the rod is perfectely elastic find
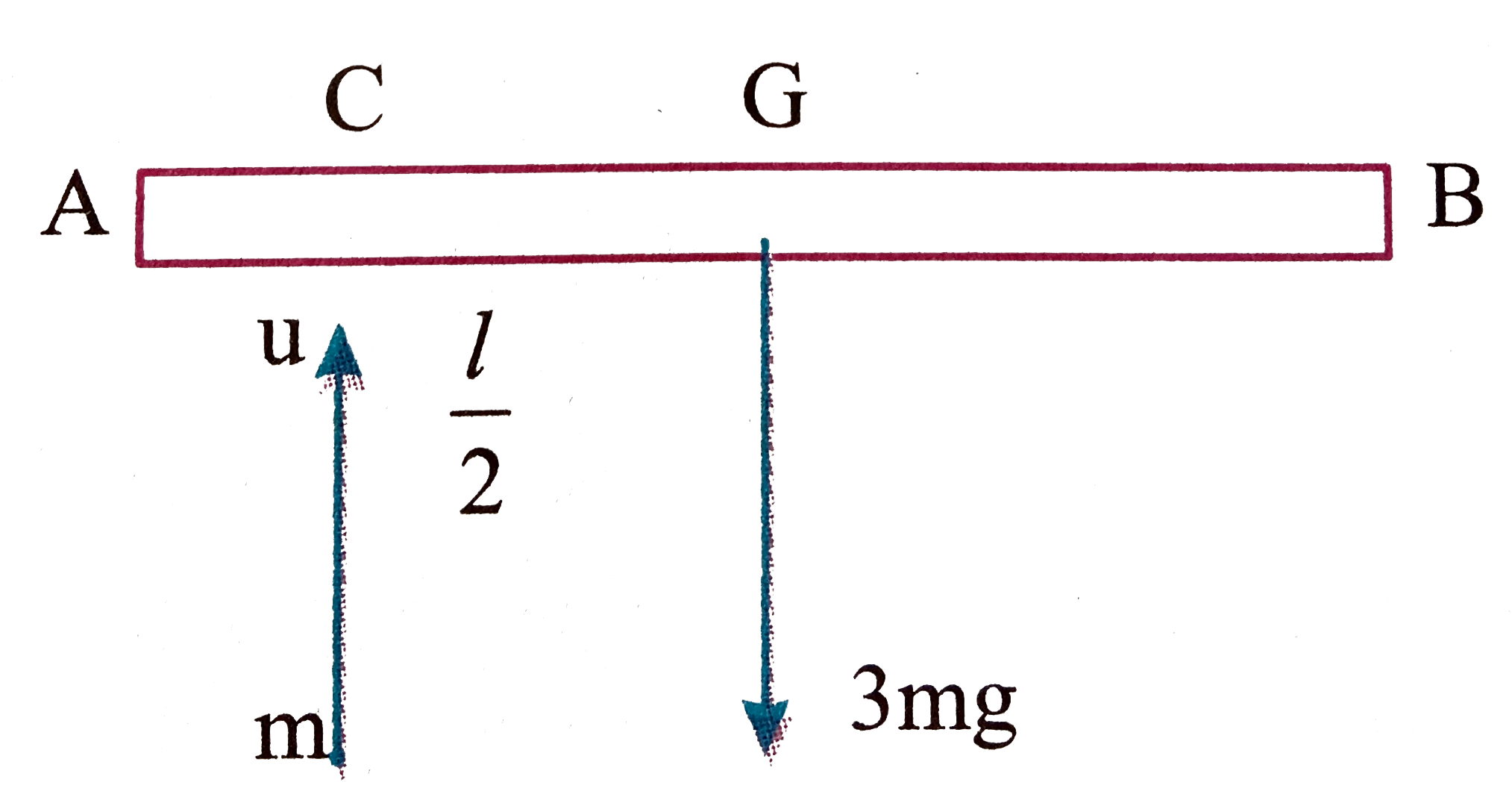
The angular velocity of the rod immediately after the impactA19u12aB12u19aC29u19aD19u29a - Question 3 - Select One
A uniform rod AB of mass m and length 2a is falling freely without rotationb under gravity with AB horizontal. Suddenly the end A is fixed when the speed of the rod is v. The angular speed which the rod begains to rotate is
Av2aB4v3aCv3aD3v4a
A rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA uniform rod AB of mass m and length 5a is free to rotate on a smooth horizontal table about a pivot through P, a point on AB such that AP = a. A particle of mass 2m moving on the table strikes AB perpendicularly at the point 2a from P with speed v, the rod being at rest. If the
coefficient of restitution between them is14 , find
their speeds immediately after impact.View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA particle is projected vertically upwards in vacuum with a speed u.
View SolutionA particle of mass m is moving with speed u. It is stopped by a force F in distance x if the stopping force is 4 F then
View Solution
