A ring of mass M and radius R is rotating with angular speed $ω$ about a fixed vertical axis passing through its centre O with two point masses each of mass $\frac{M}{8}$ at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is $\frac{8}{9} ω$ and one fo the masses is at a distance of $\frac{3}{5} R$ from O. At this instant the distance of the other mass from O is

Video Solution

Text Solution

Verified by Experts

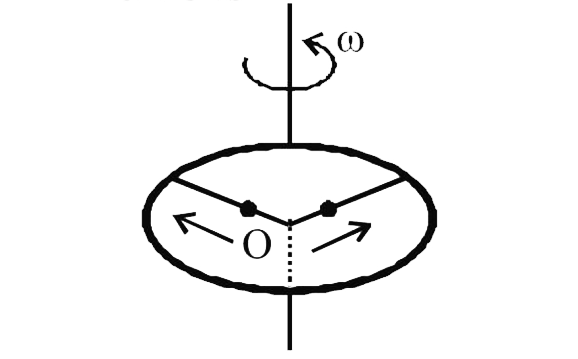
The correct Answer is:4

Using conservation of angular momentum
$m R^{2} ω = (m R^{2} \times \frac{8 ω}{9}) + (\frac{m}{8} \times \frac{9 R^{2}}{25} \times \frac{8 ω}{9}) + (\frac{m}{8} \times x^{2} \times \frac{8 ω}{9}) \Rightarrow x = \frac{4 R}{5}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid cylinder of mass M and radius R rotates about its axis with angular speed $ω$ . Its rotational kinetic energy is
A $\frac{1}{2} M R^{2} ω^{2}$
B $M R^{2} ω^{2}$
C $\frac{1}{4} M R^{2} ω^{2}$
D $\frac{1}{8} M R^{2} ω^{2}$
Question 2 - Select One
A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity $ω$ . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A $\frac{(M - 2 m) ω}{(M - m)}$
B $\frac{(M + 2 m) ω}{(M + m)}$
C $\frac{(M - 2 m) ω}{(M + m)}$
D $\frac{(M + 2 m) ω}{(M - m)}$
Question 3 - Select One
A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity $ω$ . Its kinetic energy is
A $\frac{1}{2} m r^{2} ω^{2}$
B $m r ω^{2}$
C $m r^{2} ω^{2}$
D $\frac{1}{2} m r ω^{2}$

NARAYNA-SYSTEM OF PARTICLES-Level-VI

Home
Ask Doubt
Profile