A thin rod of mass m and length 2l is placed horizontally and perpendicular to a horizontal rough nail, as shown in figure and set free. The point of contanct of the rod with the nails is l/3 distance away form the centre of rod. If the rod starts slipping when it forms an angle θ with the horizontal and the coefficient of friction of rod with nails is μ, then find μtanθ.

The correct Answer is:2

Till the rod does'tn slip the centre of mass of the rod in circular motion around the peg. Thus from COE
mg12sinθ=12lω2
Where I=4ml212+ml29=4ml29
thus ω=√3g2lsinθ
Now m13ω2=Fr−mgsinθ.......(1)
or Fr=32mgsinθ
angular acceleration of rod at an angle3 θ
mg(13)cosθ(4/9)ml2⇒α=34glcosθ
and linear acceleration of centre of mass perpendicular to rod⇒mgcosθ−N=ma from pure rolling a=(13)α
thusa=g4cosθ
⇒N=3mg4cosθ.....(ii)
μ=Fr/N=2tanθ
Topper's Solved these Questions
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V
72 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
Similar Questions
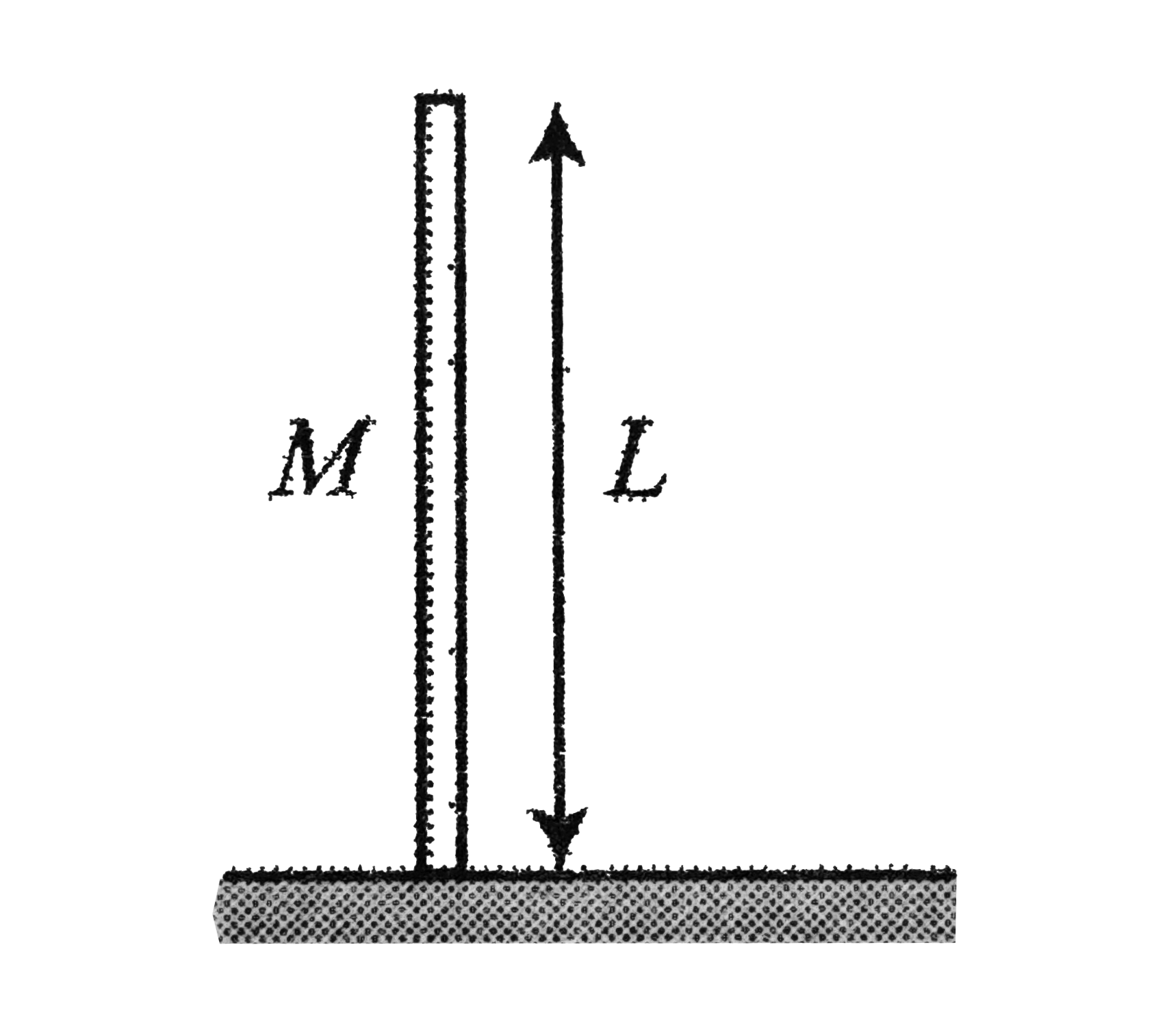
A uniform rod of mass M and length L is held vertically upright on a horizontal surface as shown in figure. Assuming zero potential energy at the base of the rod, determine the potential energy of the rod.
View SolutionA uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a/3 from the edge. The rod is released from rest. If the rod slips after it turned an angle θ, find the coefficient of friction between the rod and the table.
View Solution
Knowledge Check
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘Aπl7Bπl4Cπl12Dπl5A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What angle will the rod make with the vertical
 Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
Acos−1(gω2l)Bcos−1(2g3ω2l)Ccos−1(3g2ω2l)Dcos−1(3g4ω2l)
A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View SolutionA rod of mass m and length L , lying horizontally ils free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude LF acts on the rod at a distance of L/4 frm the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
View Solution
