
A tortoise is just sinking in water of density ρ The tortoise is assumed to be3 a hemisphere of radius R.
Q. Find the total hydrostatic force
ρgπR3
√133ρgπR3
23ρgπR3
√163ρgπR3
The correct Answer is:B
Hence the net hydrostatic force on the tortoise is
F=√F2h+F2v=√(ρgπR3)2+(23ρgπR3)2
=√133ρgπR3
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Single Answer Questions
108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - More Than One Alternative Type Question
32 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
Knowledge Check
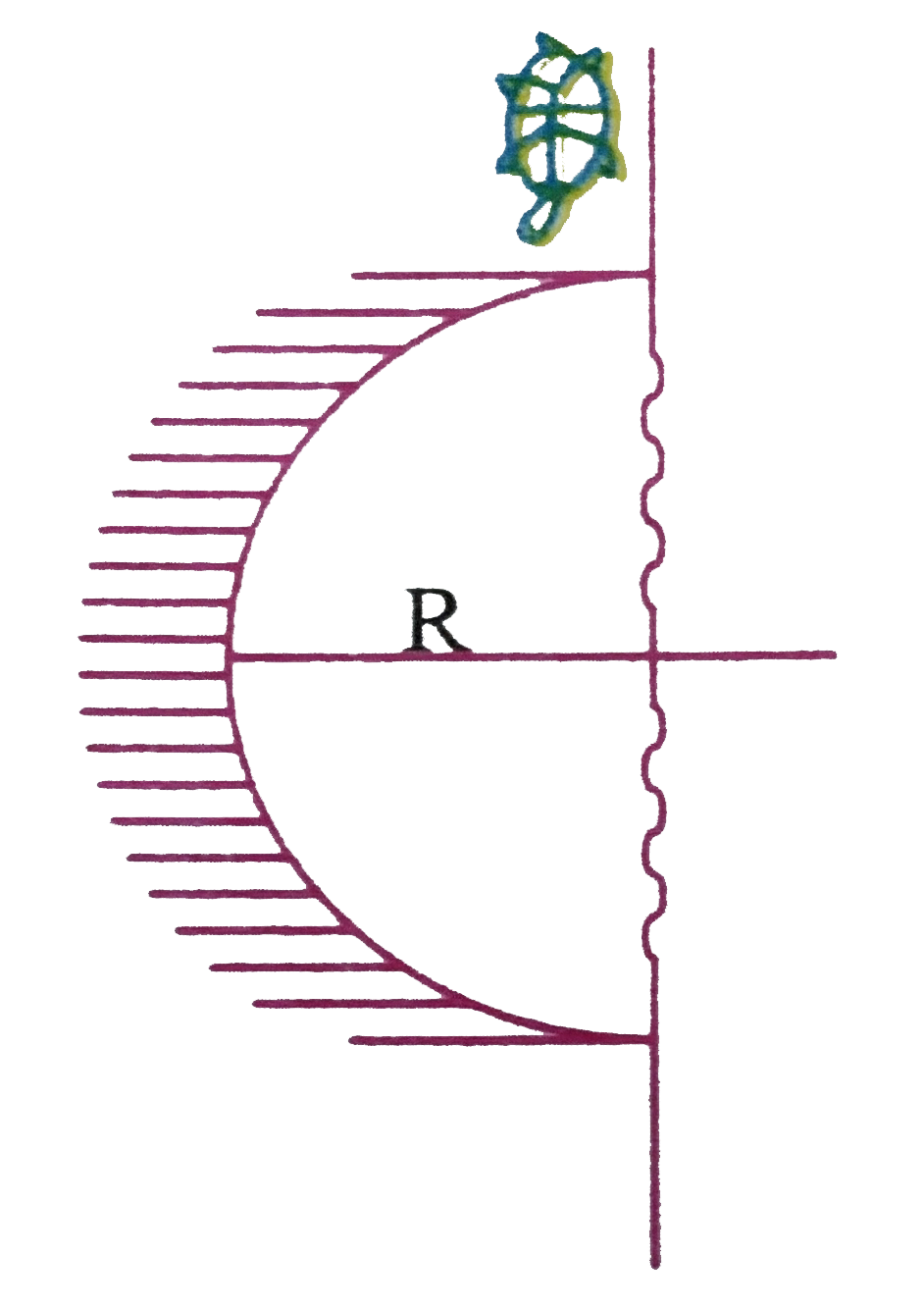
A tortoise is just sinking in water of density ρ The tortoise is assumed to be3 a hemisphere of radius R.
Find vertical thrustAρgπR3B13ρgπR3C23ρgπR3D0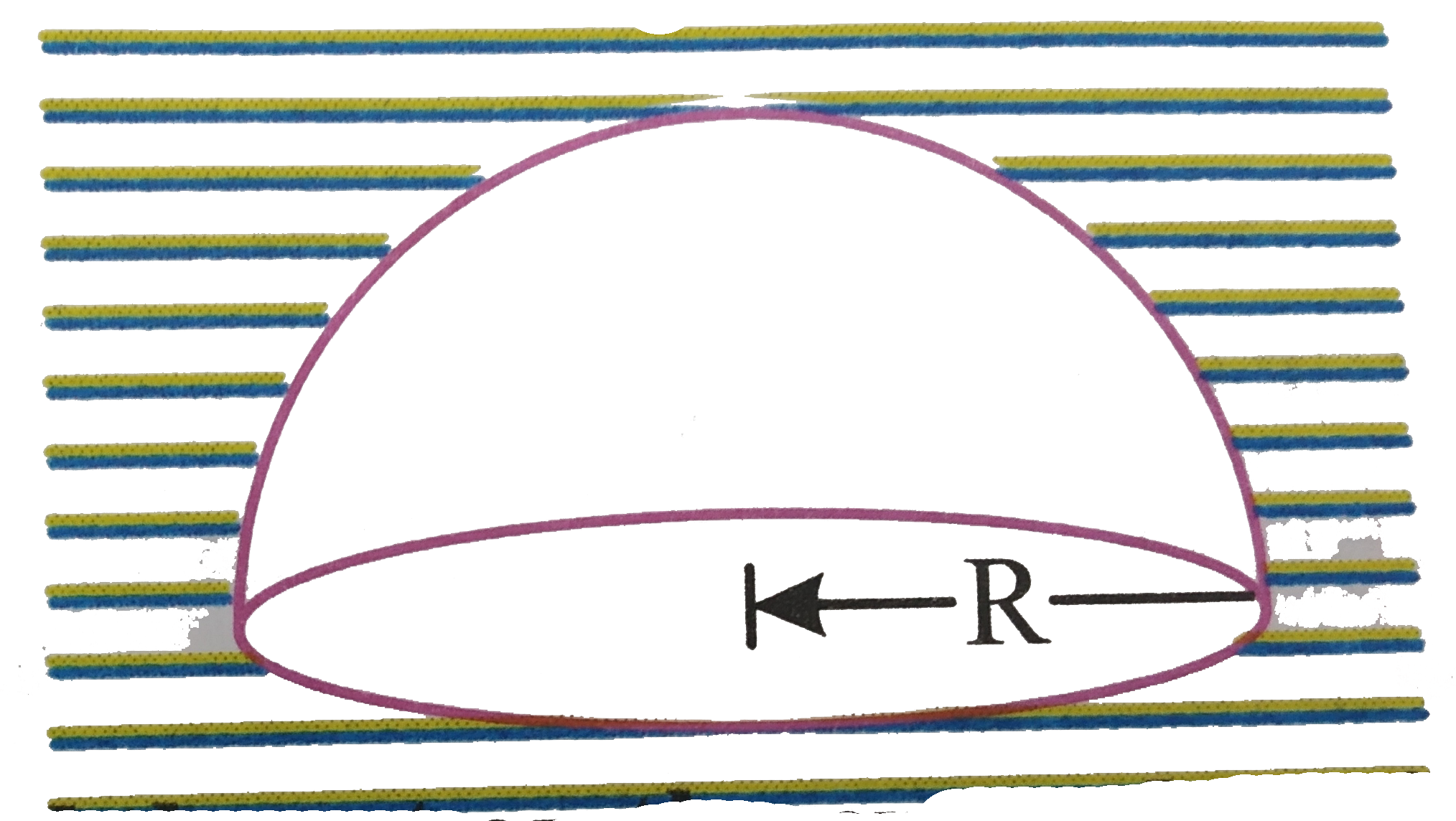
A solid hemisphere of radius R is made to just sink in a liquid of density ρ find theAπR3ρg3BπR3ρg2C0DπR3ρgA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
Aa(a2ρg+k)Ba(aρg+2k)Ca(aρg2+2k)Da(a2ρg+k2)
A solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
View SolutionA composite plate comprises a triangular area (1) and rectangular area (2) as shown in the figure. The triangular plate experiences forces due to the liquids of densities ρ1 and the rectangular plate experiences the force due to liquid of density ρ2. Find the hydrostatic forces on (a) area 1, (b) area 2, (c) total composite area of the plate. Assume ρ1=ρ and ρ2=2ρ.

View Solution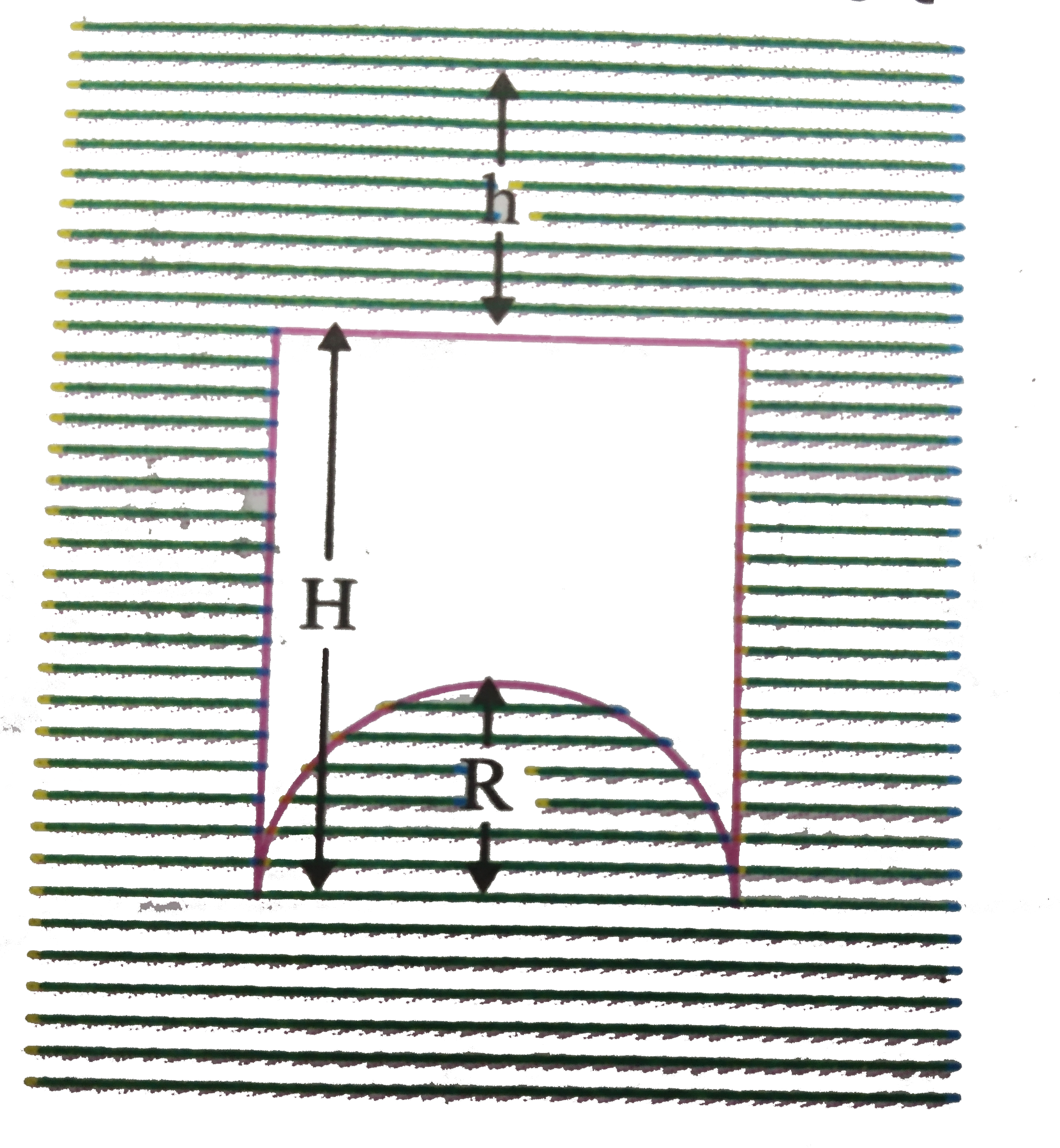
A cylinder of radius R, height H and density simga has a hemispherical cut at its bottom. The top of the cyliner is kept at depth h from the liquid surface. If the density of liquid is ρ, find the hydrostatic force acting on the hemispherical surface of the cylinder.
View SolutionA solid glass hemisphere of density d and radius R lies (with curved surface of hemisphere below the flat surface) at the bottom of a tank filled with water of density ρ such that the flat surface of hemisphere is H depth below the liquid surface. Weight of water + tank is W1 and that of hemisphere is'W2. W Then choose the incorrect options
View SolutionA mango tree is at the bank of a river and one of the branch of tree extends over the river. A tortoise lives in the river. A mango falls just ono the tortoise. The acceleration of the mango falling from tree as it appears to the tortoise is (refractive index of water is 4/3 and the tortoise is stationary)
View Solution
