Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and thired plates are maintained at temperatures 2T and 3T respectively Find the temperature of the middle (i.e second) plate under steady state .
Let T1 is the temperature of the middlte plate Under steady rate of emission =rate of absorption
σ(2A)(T1)4=σA(2T)4+σA(3T)4
2T_(1)^(4) = 16T^(4) + 81T^(4) rArr T_(1) = ((97)/(2))^(¼) T
 .
.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - C .U .Q89videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL -1 (C.W)1videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise187videos
THERMODYNAMICS
- BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION23videos
UNITS AND MEASUREMENTS
Similar Questions
Three very large plates of same area are kept parallel equispaced and close to each other. They are considered as ideal black surfaces and have very high thermal conductivity. The first and third plates are maintained at temperature 3R and 2R, respectively. What will be the value of n4 if the temperature of the middle (i.e., second) plane under steady state condition is nT.
View SolutionThree large identical plates are kept close and parallel to each other. The outer two plates are maintained at temperatures T and 2T. respectively. The temperature of the middle plate in steady state will be close to
View Solution
Knowledge Check
- Question 1 - Select One
Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and third plates are maintained at temperatures 2T and 3T respectively Find the temperature of the middle (i.e second) plate under steady state .
A(652)1/4TB(974)1/4TC(972)1/4TD(97)1/4T - Question 2 - Select One
Three identical metal plates with large surface areas are kept parallel to each other as shown. The left most is given a charge Q, the right most part a charge −2Q and the middle one remains neutral. Then which is wrong-
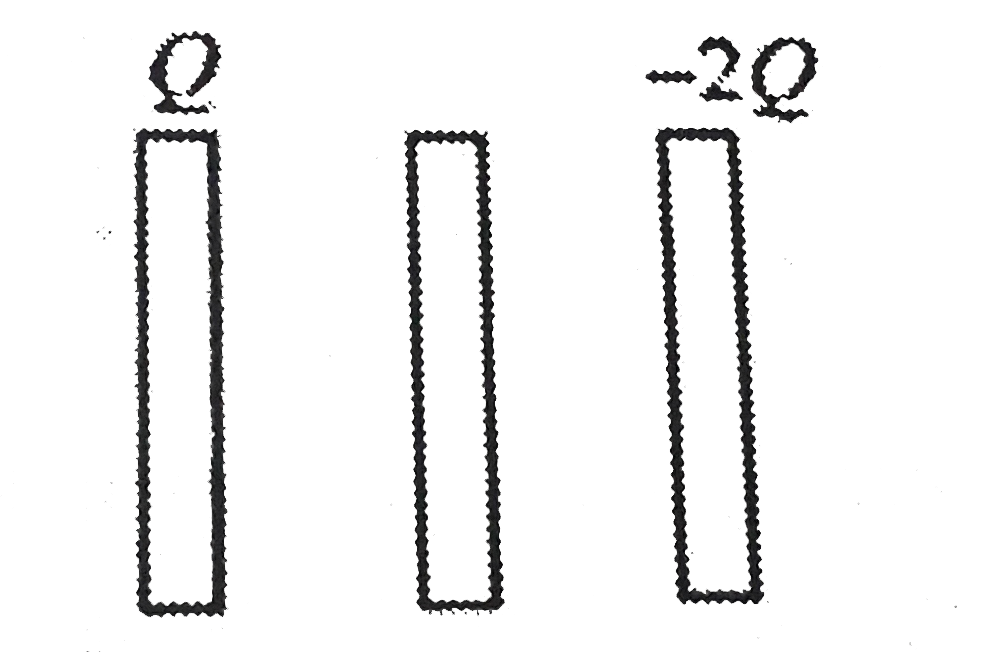 AThe charge appearing on outer surface of right most plate is −Q2BThe charge appearing on outer surface of left most plate is −Q2CThe charge appearing on left surface of middle plate is −3Q2DThe charge appearing on right surface of middle plate is 3Q4
AThe charge appearing on outer surface of right most plate is −Q2BThe charge appearing on outer surface of left most plate is −Q2CThe charge appearing on left surface of middle plate is −3Q2DThe charge appearing on right surface of middle plate is 3Q4 - Question 3 - Select One
Two plates of same area are placed in contact. Their thickness as well as thermal conductivities are in the ratio 2:3. The outer surface of one plate is maintained at 10∘C and that of the other at 0∘C. What is the temperature at the common surface?
A0∘CB2.5∘CC5∘CD6.5∘C
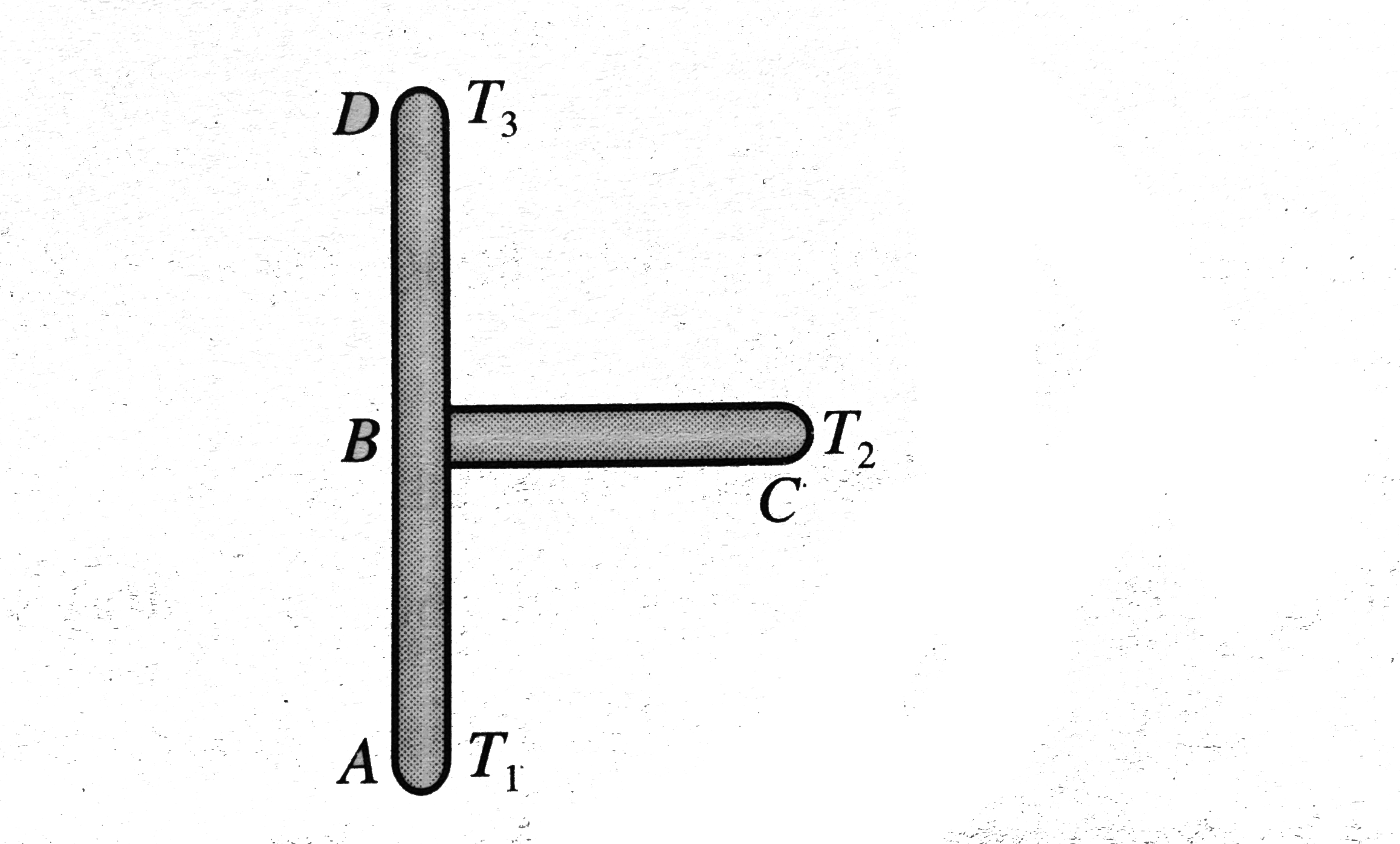
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
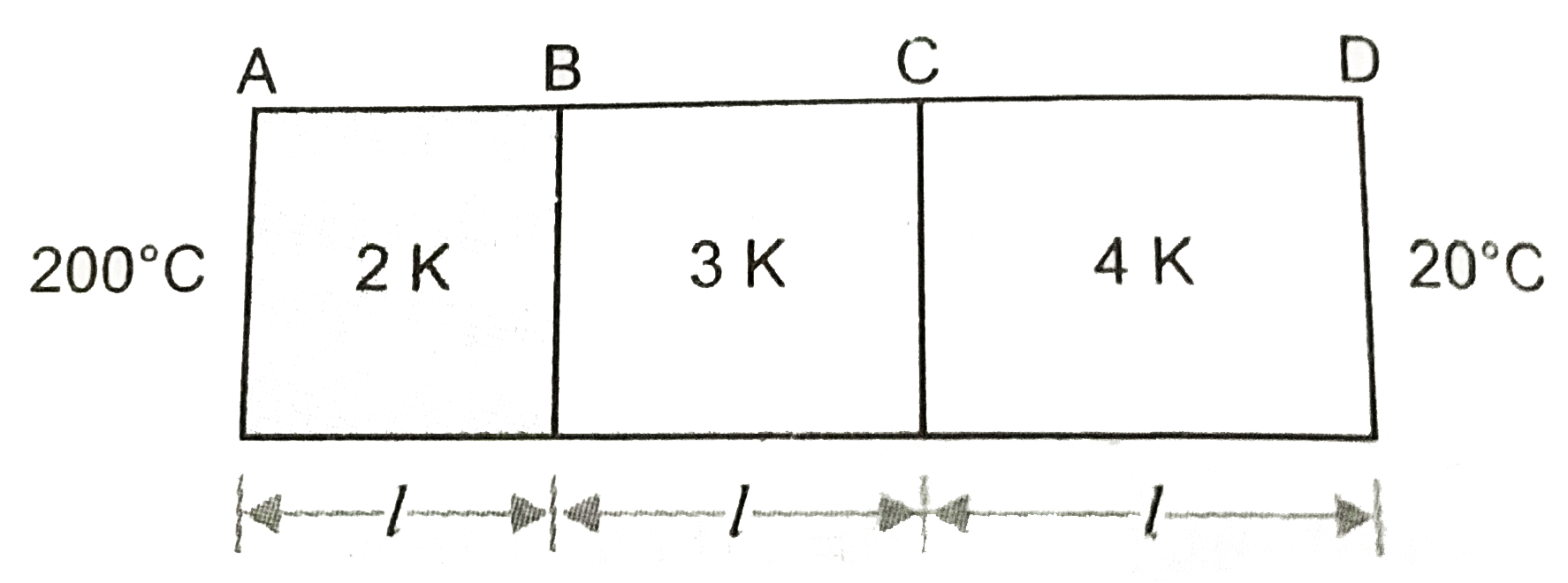 .View Solution
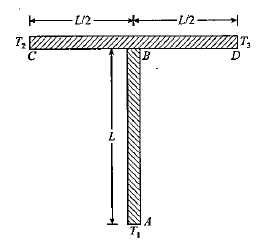
.View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
 View Solution
View SolutionThe plane surface of two sheets of different metals are kept in contact with each other. The thickness of sheets 2.5cm and 3 cm respectively and the ratio of their thermal conductivities in the same order is 5:6. If the outer surfaces of the sheets are at constant temperatures of 100∘C and 10∘C respectively, calculate the temperature of interface.
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod isView Solution

