Three large identical plates are kept close and parallel to each other. The outer two plates are maintained at temperatures T and 2T. respectively. The temperature of the middle plate in steady state will be close to
1.1 T
1.3 T
1.7 T
1.9 T
To find the temperature of the middle plate in a steady state when three large identical plates are kept parallel to each other, with the outer plates at temperatures T and 2T, we can use the principles of heat transfer and the Stefan-Boltzmann law.
1. Identify the Temperatures:
- Let the temperature of the first plate (outer) be T1=T.
- Let the temperature of the third plate (outer) be T3=2T.
- Let the temperature of the middle plate be T2.
2. Assume Steady State:
- In steady state, the rate of heat loss from the middle plate must equal the rate of heat gain from the outer plates.
3. Apply Stefan-Boltzmann Law:
- The heat transfer due to radiation can be expressed using the Stefan-Boltzmann law:
Q=σA(T4)
- Here, σ is the Stefan-Boltzmann constant, and A is the area of the plates.
4. Calculate Heat Loss from the Middle Plate:
- The middle plate loses heat to both outer plates. Therefore, the total heat loss from the middle plate can be written as:
Qloss=2σAT42
5. Calculate Heat Gain by the Outer Plates:
- The first plate (at temperature T) gains heat from the middle plate:
Qgain, 1=σAT4
- The third plate (at temperature 2T) also gains heat from the middle plate:
Qgain, 3=σA(2T)4=σA⋅16T4
- Therefore, the total heat gain by the outer plates is:
Qgain=σAT4+σA⋅16T4=σA(1+16)T4=σA⋅17T4
6. Set Heat Loss Equal to Heat Gain:
- In steady state, we have:
2σAT42=σA⋅17T4
- We can cancel σA from both sides:
2T42=17T4
7. Solve for T2:
- Rearranging gives:
T42=172T4
- Taking the fourth root:
T2=(172)1/4T
8. Approximate the Value:
- Calculate (172)1/4:
172=8.5⇒√(4)8.5≈1.7
- Thus, we find:
T2≈1.7T
Final Answer:
The temperature of the middle plate in steady state will be approximately 1.7T.
- Let the temperature of the first plate (outer) be T1=T.
- Let the temperature of the third plate (outer) be T3=2T.
- Let the temperature of the middle plate be T2.
- In steady state, the rate of heat loss from the middle plate must equal the rate of heat gain from the outer plates.
- The heat transfer due to radiation can be expressed using the Stefan-Boltzmann law:
Q=σA(T4)
- Here, σ is the Stefan-Boltzmann constant, and A is the area of the plates.
- The middle plate loses heat to both outer plates. Therefore, the total heat loss from the middle plate can be written as:
Qloss=2σAT42
- The first plate (at temperature T) gains heat from the middle plate:
Qgain, 1=σAT4
- The third plate (at temperature 2T) also gains heat from the middle plate:
Qgain, 3=σA(2T)4=σA⋅16T4
- Therefore, the total heat gain by the outer plates is:
Qgain=σAT4+σA⋅16T4=σA(1+16)T4=σA⋅17T4
- In steady state, we have:
2σAT42=σA⋅17T4
- We can cancel σA from both sides:
2T42=17T4
- Rearranging gives:
T42=172T4
- Taking the fourth root:
T2=(172)1/4T
- Calculate (172)1/4:
172=8.5⇒√(4)8.5≈1.7
- Thus, we find:
T2≈1.7T
The temperature of the middle plate in steady state will be approximately 1.7T.
Topper's Solved these Questions
Similar Questions
Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and thired plates are maintained at temperatures 2T and 3T respectively Find the temperature of the middle (i.e second) plate under steady state .
View SolutionThree very large plates of same area are kept parallel equispaced and close to each other. They are considered as ideal black surfaces and have very high thermal conductivity. The first and third plates are maintained at temperature 3R and 2R, respectively. What will be the value of n4 if the temperature of the middle (i.e., second) plane under steady state condition is nT.
View Solution
Knowledge Check
- Question 1 - Select One
Three very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and third plates are maintained at temperatures 2T and 3T respectively Find the temperature of the middle (i.e second) plate under steady state .
A(652)1/4TB(974)1/4TC(972)1/4TD(97)1/4T - Question 2 - Select One
Two large metal plates are placed parallel to each other The inner surfaces of plates are charge by +σand−σ(Cm−2) The outer surfaces are neutral .The electric field in the negion between the plates and outside the plates is
A2σε0,σε0Bσε0, zeroC2σε0, zeroDzero , 2σε0 - Question 3 - Select One
Three large identical conducting plates of area A are closely placed parallel to each other as shown (the area A is perpendicular to plane of diagram). The net charge on left, middle and right plates are QL,QM and QR respectively. Three infinitely large parallel surface SL,SM and SR are drawn passing through middle of each plate such that surface are perpendicular to plane of diagram as shown. Then pick up the correct option(s).
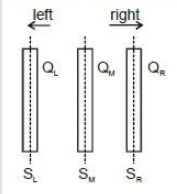 AThe net charge on left side of surface SL is equal to net charge on right side of surface SRBThe net charge on left side of surface SL is equal to net charge on right side of surface SMCThe net charge on left side of surface SL is equal to net charge on right side of surface SLDThe net charge on right side of surface SL is equal to net charge on left side of surface SR
AThe net charge on left side of surface SL is equal to net charge on right side of surface SRBThe net charge on left side of surface SL is equal to net charge on right side of surface SMCThe net charge on left side of surface SL is equal to net charge on right side of surface SLDThe net charge on right side of surface SL is equal to net charge on left side of surface SR
Three identical metallic plates are kept parallel to one another at a separation of a and b. The outer plates are connected by a thin conducting wire and a charge Q and 3Q is placed on the central plate and left plate respectively. Find electric field at P.
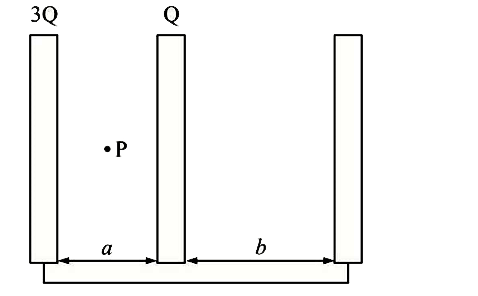 View Solution
View SolutionTwo conducting plates each having area A are kept at a separation d parallel to each other. The two plates are con- nected to a battery of emf V. The space between the plates is filled with a liquid of dielectric constant K. The height (x) of the liquid between the plates increases at a uniform rate from zero to d in a time interval t0.
(a) Write the capacitance of the system as a function of x as the liquid beings to fill the space between the plates.
(b) write the current through the cell at time t
 View Solution
View SolutionThree large plates A, B and C are placed parallel to each other and charges are given as shown. The charge that appears on the left surface of plate B is
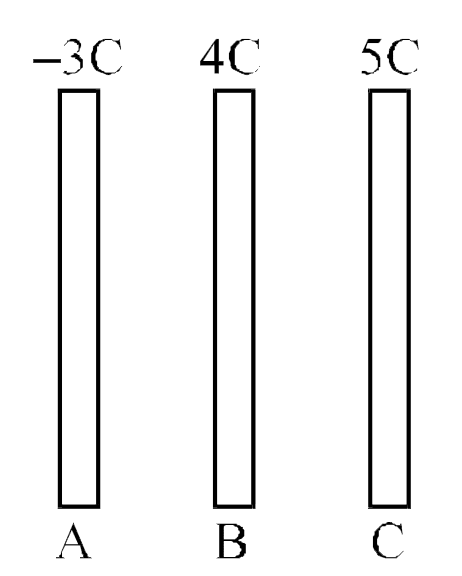 View Solution
View SolutionThree identical metallic plates are kept parallel to one another at separations a and b. The outer plates are connected to the ground and the middle plate is given charge Q. Then, the charge on the right side of middle plate is
 View Solution
View SolutionTwo large conducting plates are placed parallel to each other with a separation of d between them. An electron starting from rest near one of the plates reaches the other plate in time t. If e is the charge on the electron and m is its mass, then the surface charge density on the inner surface is
View Solution

