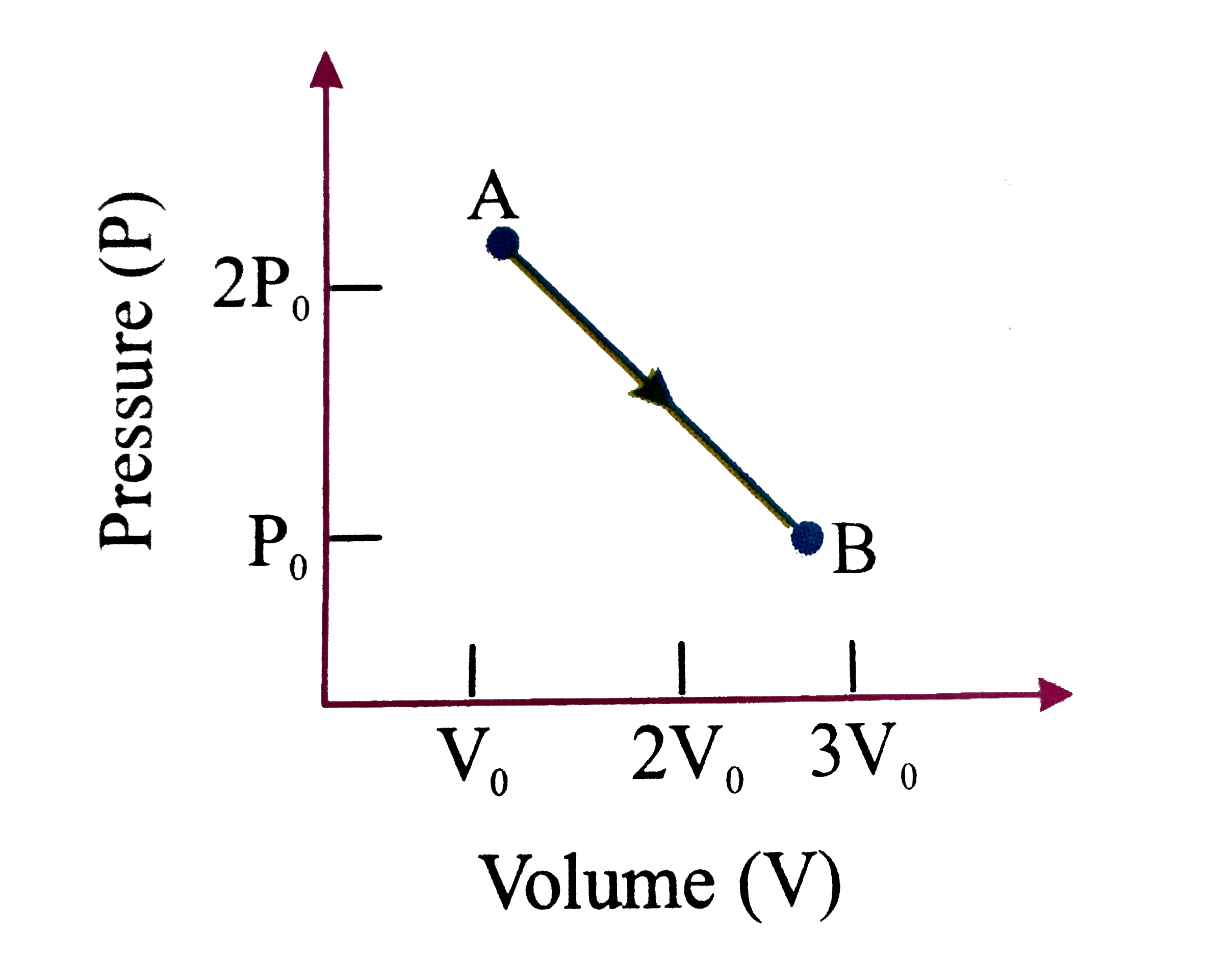
Determine the average molar heat capacity of an ideal gas under going a process shown in fig.

A

$(\frac{γ - 1}{γ - 1}) R$

B

$(\frac{3 γ - 2}{γ - 1}) R$

C

$(\frac{γ - 2}{γ - 4}) R$

D

$(\frac{γ + 1}{γ - 1}) R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let n be the number of moles of the gas,
then $T_{A} = \frac{2 P_{0} V_{0}}{n R} and T_{B} = \frac{3 P_{0} V_{0}}{n R}$
Now, work done by the gas during the proces is given by area under curve
$Δ W = \frac{1}{2} (P_{0} + 2 P_{0}) (3 V_{0} - V_{0}) = 3 P_{0} V_{0}$
work done per mole of the gas per unit rise in temperature.
$W^{1} = \frac{Δ W}{n Δ T} = \frac{Δ W}{n (T_{B} - T_{A})}$ ,
$= \frac{3 P_{0} V_{0}}{n [\frac{3 P_{0} V_{0}}{n R} - \frac{2 P_{0} V_{0}}{n R}]} = 3 R$
Molar heat capacity of the gas for the above process will be
$C = C_{v} + W' = \frac{R}{γ - 1} + 3 R = (\frac{3 γ - 2}{γ - 1}) R$

|

Updated on:21/07/2023

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
The molar heat capacity for an ideal gas cannot
Abe negative
Bbe equal to either $C_{V}$ or $C_{P}$
Clie in the range $C_{V} \leq C \leq C_{P}$
Dit may have any value between $- \infty$ and $+ \infty$
Question 2 - Select One
Molar heat capacity of a gas is
AExtensive property
BIntensive property
CChemical property of gas
DColligative property
Question 3 - Select One
The molar heat capacity of a gas in a process
Ais either $C_{V} or C_{P}$
Blies between $C_{V} or C_{P}$
Cmay range from zero to infinity
Dcan have any real value

NARAYNA-THERMODYNAMICS-Exercise

Home
Ask Doubt
Profile