A vertical cylinder of cross-section area A contains one mole of an ideal mono-atmic gas under a piston of mass M At a certain instant a heater which supplies heat at the rate q J/s is switched ON under the piston. The velocity with which the piston moves upward under the condition that pressure of gas remains constant is [Assume on heat transfer through walls of cylinder]
![A vertical cylinder of cross-section area A contains one mole of an ideal mono-atmic gas under a piston of mass M At a certain instant a heater which supplies heat at the rate q J//s is switched ON under the piston. The velocity with which the piston moves upward under the condition that pressure of gas remains constant is [Assume on heat transfer through walls of cylinder]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NAR_PHY_XI_V06_C02_E01_095_Q01.png)
constant and equal to 25×qp0A+Mg
constant and equal to 35×qp0A+Mg
varying
constant but can't be determined from given information.
The correct Answer is:A
From equilibrium of piston, pA=p0A+Mg where P is presseure of gas.
From first law of thermodynamics Q=ΔU+W
∫nCpdT=∫nCvdT+∫pdV
nCpΔT=nCvΔT+∫pAdx
n×5R2ΔT−n×32RΔT=∫pAdx
∫pAdx=1×RΔTAlsoQ=∫qdt
So, ∫pAdx=∫qdt−32RΔT⇒qdt=52pAdx
⇒dxdt=25×qpA=25×qp0A+Mg
Topper's Solved these Questions
Similar Questions
A vertical cylinder pistion system has cross-section S. It contains 1 mole of an ideal monoatomic gas under a pistion of mass M.At a certain instant a heater is switched on which transmits a heat Q per unit constant and the system is thermally insulated.
View SolutionTwo moles of an ideal monoatomic gas are contained in a vertical cylinder of cross sectional area A as shown in the figure. The piston is frictionless and has a mass m. At a certain instant a heater starts supplying heat to the gas at a constant rate qJ/s. Find the steady velocity of the piston under isobaric condition. All the boundaries are thermally insulated.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
A375KB425KC475KD515K - Question 2 - Select One
A resistance coil, connected to an external battery is placed inside an adiabatic cylinder filled with frictionless piston of mass m and containing an ideal gas. A current i flows through the coil, which has resistance R. The speed with which the piston must move in order to keep the temperature of the gas constant will be
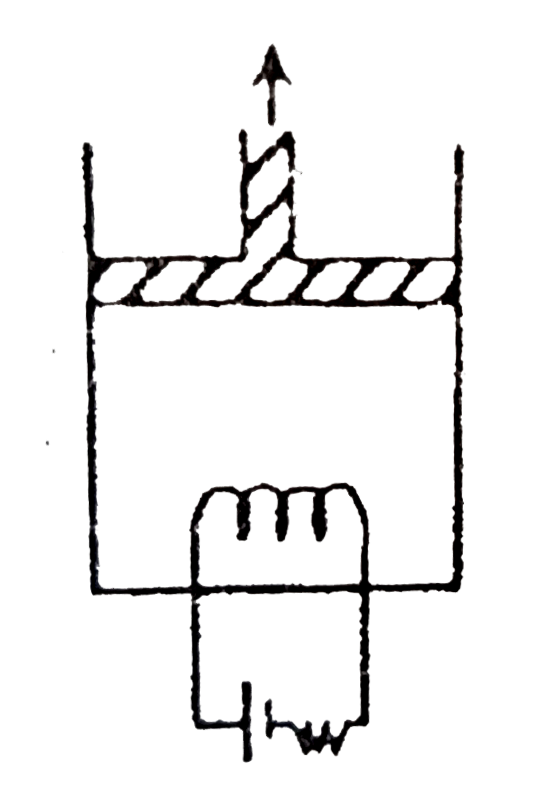 Ai2R/mgBiR/mgC0DData is insufficient.
Ai2R/mgBiR/mgC0DData is insufficient. - Question 3 - Select One
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (figure). If the temperature is increased
 Aboth p and v of the gas will changeBonly p will increase according to Charles' lawCV will change but not pDp will change but not V
Aboth p and v of the gas will changeBonly p will increase according to Charles' lawCV will change but not pDp will change but not V
A Perfect gas is enclosed in a vertical cylinder filled with a piston of mass m. The gas is heated by passing constant current I through a heating coil of resistance R placed inside the cylinder. At what speed v must the piston move upward in order that temperature of the gas may remain unchanges? Assume ideal insulating walls and piston and there is no fusion.
View SolutionA horizontal cylinder has two sections of unequal cross - sections, in which two pistons can move freely. The pistons are joined by a string, Some gas is trapped between the pistons. If this gas is heated the pistons will
 View Solution
View SolutionOne mole of a certain ideal gas is contained under a weight-less piston of a vertical cylinder at a temperature T. The space over the piston opens into the atmosphere. What work has to be performed on order to increase isothermally the gas volume under the piston n times by slowly raising the piston ? The friction of the piston against the cylinder walls is negligibly small.
View SolutionA cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (figure). If the temperature is increased
 View Solution
View SolutionA heating element of piston resistance r is fitted inside an adiabatic cylinder which carries a frictionless piston of mass m and crosssection A as shown in diagram. The cylinder contains one mole of an ideal diatomic gas. The current flows through the element such that the temperature rises with time t as ΔT=alpaht+12βt2? (α and β are constants), while pressure remains constant. The atmospheric pressure above the piston is P0. Then
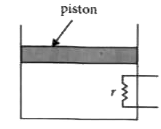 View Solution
View Solution

