From the above figure the values of stopping potentials for M1 and M2 for a frequency v3(>v02) of the incident radiatioins are V1 and V2 respectively. Then the slope of the line is equal to
V2−V1v02−v01
V1−V2v02−v01
V2v02−v01
V1v02−v01
The correct Answer is:B
hv01+eV1=hv02+eV2e(V1−V2)=h(V02−V01),he=(V1−V2)(V02−V01)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - NCERT BASED QUES.26videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-V31videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (C.W)20videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -443videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
The stopping potential (v0) varies linearly with the frequency (v)of the incident radiation for a given photosensitive surface with the slope remaining the same for different surface . Given reason.
View SolutionDraw a plot showing the variation of photoelectric current with collector plate potential for two different frequencies, v1>v2, of incident radiation having the same intensity. In which case will the stopping potential be higher ? Justify your answer.
View Solution
Knowledge Check
- Question 1 - Select One
Figure show the variation of the stopping potential (V0) with the frequency (v) of the incident radiations for two different photosensitive matererial M1 and M2 What are the values of work functions for M1 and M2 respectively
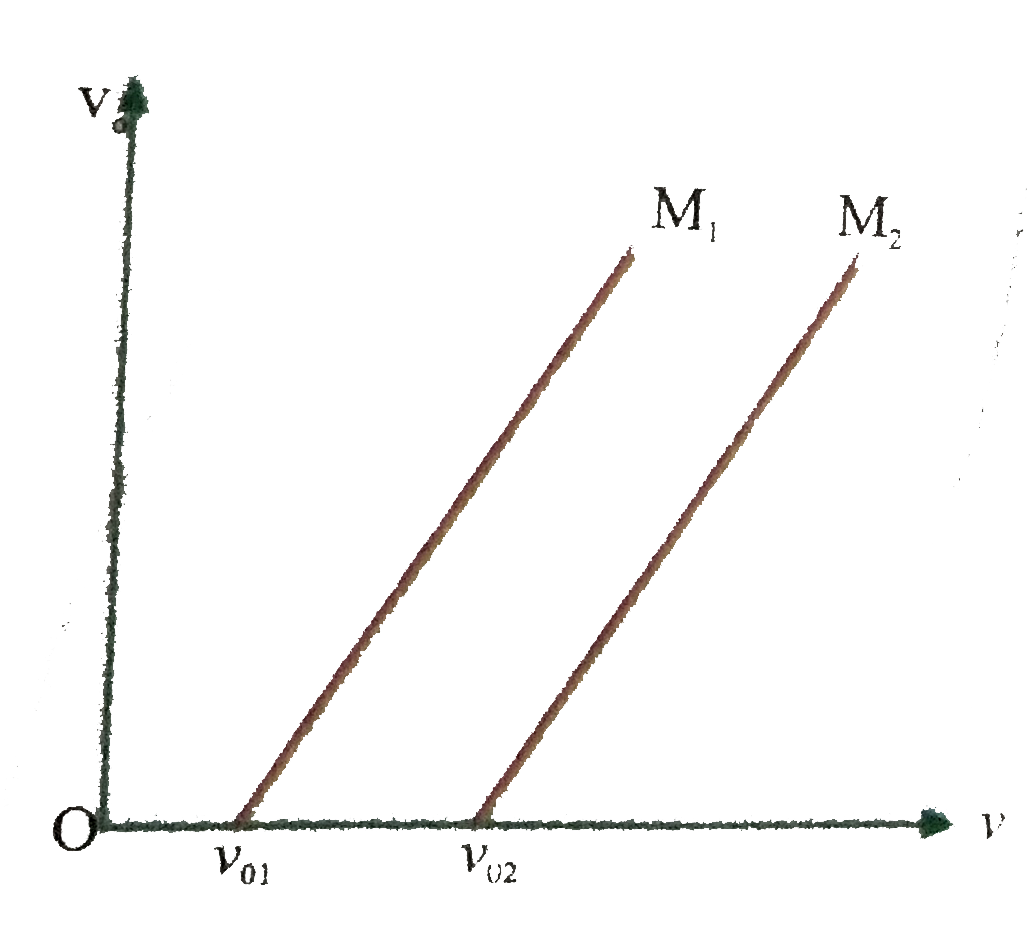 Ahv01,hv02Bhv02,hv01Chv01,hv01Dhv02,hv02
Ahv01,hv02Bhv02,hv01Chv01,hv01Dhv02,hv02 - Question 2 - Select One
From the graph shown, the value of work function if the stopping potential (V), and frequency of the incident light vare on y and x-axes respectively is
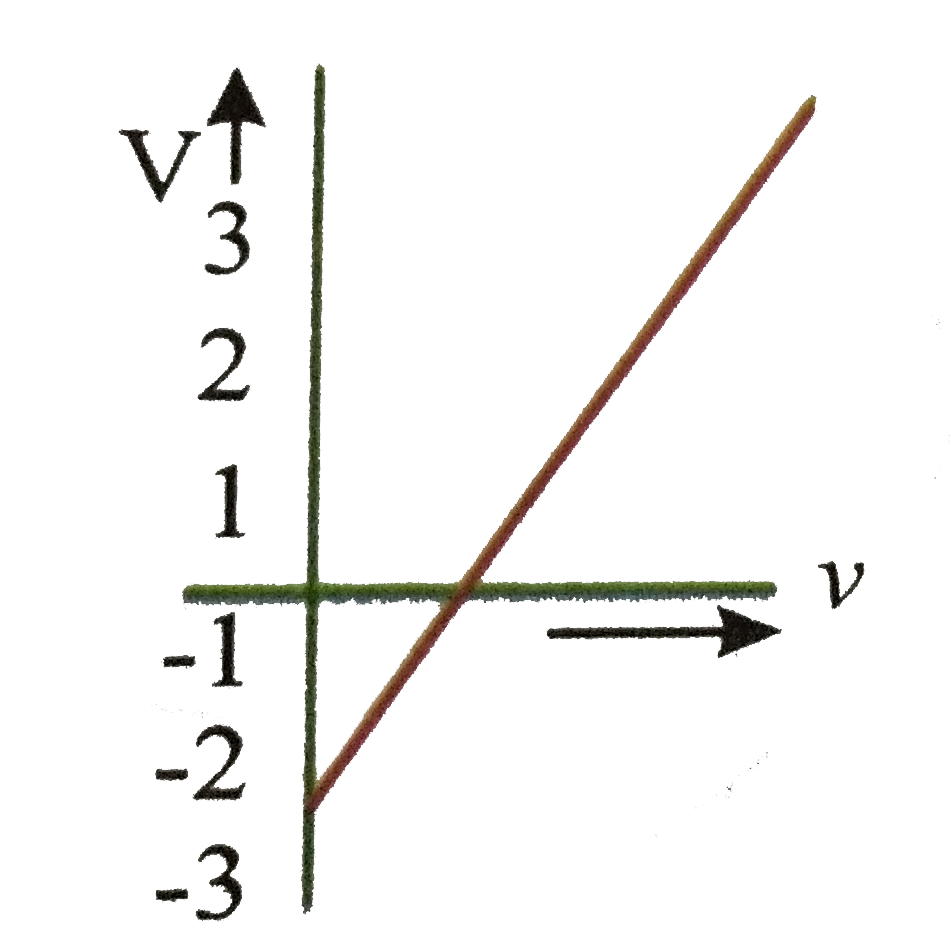 A1eVB2eVC3eVD4eV
A1eVB2eVC3eVD4eV - Question 3 - Select One
The stopping potential are V1 and V2. Calculate the (V1−V2), if the λ1 and λ2 are wavelength of incident lights, respectively.
Ahce(1λ1−1λ2)Bhce(1λ1+1λ1)Cehc(1λ1+1λ2)Dehc(1λ1−1λ2)
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
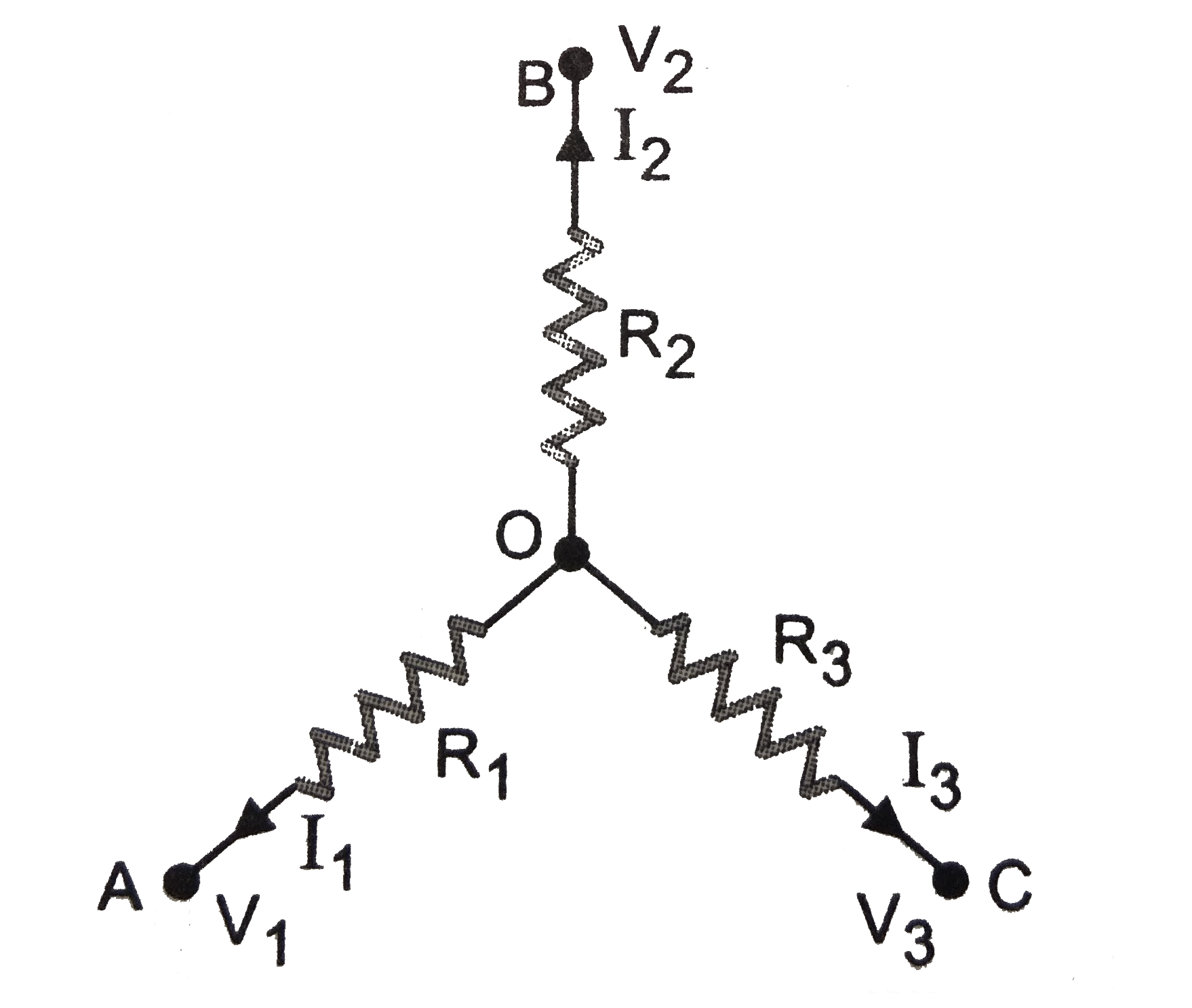 View Solution
View SolutionIn photoelectric effect the slope of straight line graph between stopping potential (Vs) and frequency of incident light (v) gives
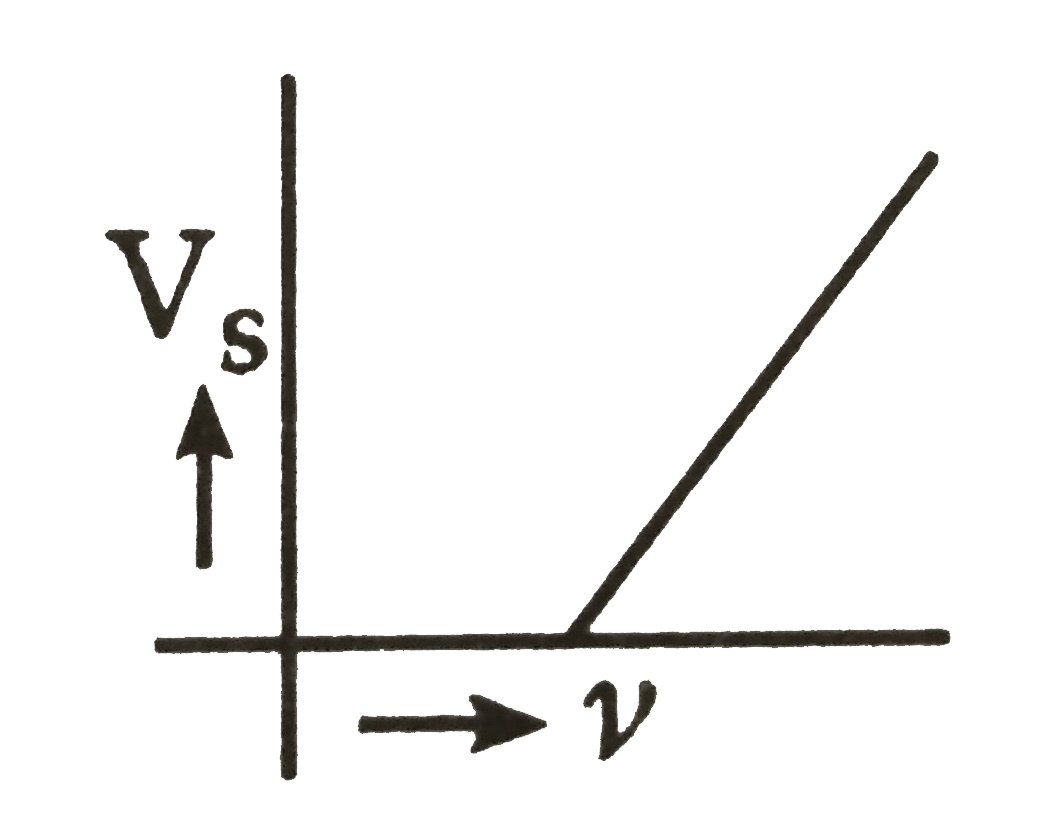 View Solution
View SolutionGraph plotted between stopping potential V0 and frequency v, where v>v0, for a photosensitive material is a_____graph whose slope is ____.
View SolutionThe variation of the stopping potential (V0) with the frequency (v) of the light incident on two different photosensitive surfaces M1andM2 is shown in the figure. Identify the surfaces which has greater value of the work function.
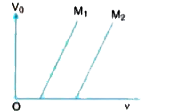 View Solution
View SolutionIn photoelectric effect, stopping potential for a light of frequency n1 is V1. If light is replaced by another having a frequency n2 then its stopping potential will be
View Solution

