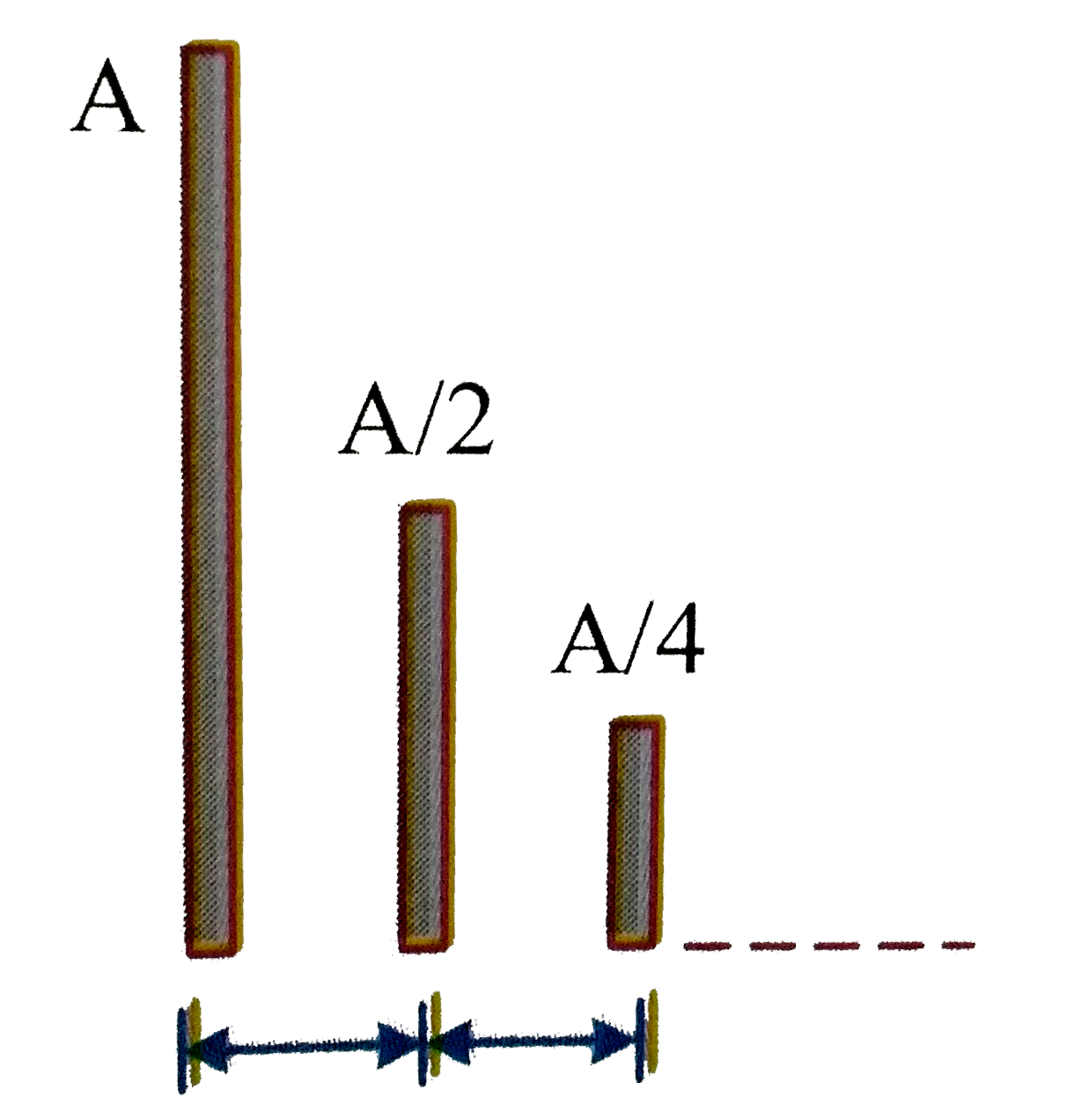
n conducting plates are placed face to face. Distance between two consecutive plates is d.
Area of plates is A,A2,A4,A8....(12n−1)A
A dielectric slab of dielectric constant k is inserted between the first and second plates and the assembly is charged by a battery of emfξ. Find the charge stored in the assembly.
 .
.
ε0Aξ2d[1k+2n−1−2]
ε0Aξ2d[1k+2n−1−1]
ε0Aξd[1k+2n−1−2]
ε0Aξ3d[1k+2n−1−2]
The correct Answer is:A
(n−1) capacitors are in series, So,
1C=1ε0A/2d+1ε0A/4d+...+1ε0A/2n−1ds
Ceq=ε0A2d[1k+2n−1−2]
∴q=Ceqξ⇒1=ε0Aξ2d[1k+2n−1−2]
V1=30VandV2=30V (Conceptual).
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-VI28videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Subjective9videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - NCERT Based13videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -447videos
ATOMS
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
Similar Questions
Find the charge on each plate given area of each plate is A and separation between two consecutive plates is d.
 View Solution
View SolutionIntroduction of a dielectric slab of dielectric constant K between the plates |When the battery is disconnected |When the battery remains connected |Questions |Force between capacitor plates
View Solution
Knowledge Check
- Question 1 - Select One
n conducting plates are placed face to face. Distance between two consecutive plates is d.
Area of plates is A,A2,A4,A8....(12n−1)A
A dielectric slab of dielectric constant k is inserted between the first and second plates and the assembly is charged by a battery of emfξ. Find the charge stored in the assembly.
 .Aε0Aξ2d[1k+2n−1−2]Bε0Aξ2d[1k+2n−1−1]Cε0Aξd[1k+2n−1−2]Dε0Aξ3d[1k+2n−1−2]
.Aε0Aξ2d[1k+2n−1−2]Bε0Aξ2d[1k+2n−1−1]Cε0Aξd[1k+2n−1−2]Dε0Aξ3d[1k+2n−1−2] - Question 2 - Select One
The separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
Aε0Ad−x(1−1K)Bε0Ad+x(1−1K)Cε0Ad+x(1+1K)Dε0Ad−x(1+2K) - Question 3 - Select One
A parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
Athe stored energy remains unchanged.Bthe stored energy is increased by a factor of 2.Cthe stored energy is reduced to half its previous value.Dnone of the above is correct.
A dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionTwo dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.
 View Solution
View SolutionSuppose n conducting face to face, and the distance between two successive plates is d. Each plate is half of the area of the previous one. If area of first plate is A
 .
.
(i) If the area of the first plate is A, find the equyivalent capacitance of the system.
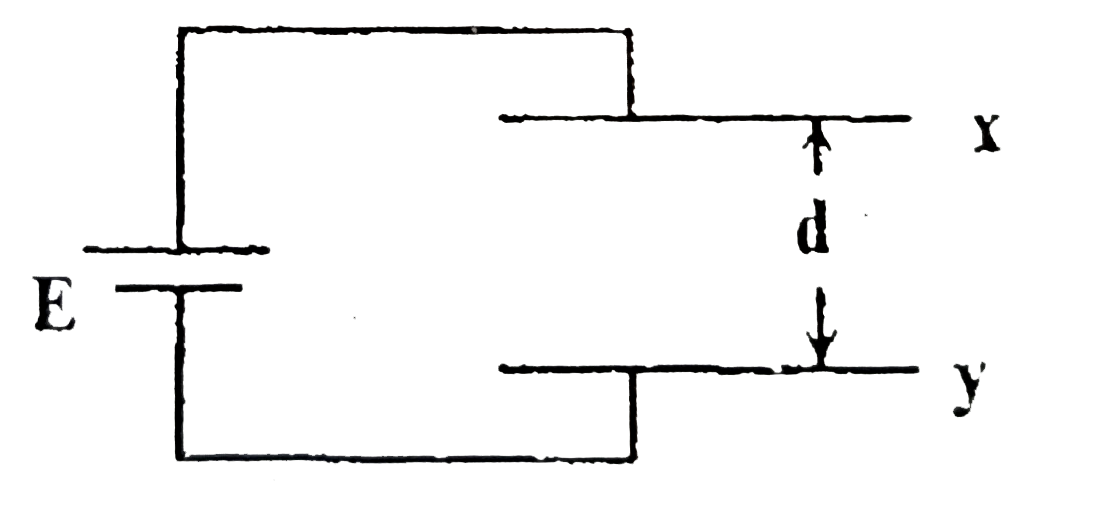
(ii) If a cell of emf V is connected as shown in and a dielectric of dielectric constant k is inserted between the first and second plates, dind the charge on the nth plate.View SolutionA parallel-plate capacitor has plate area A, the distance between its two plates x and y is d and a dielectric slab of dielectric constant εr is filled between the regions. It is connected to a cell of emf E. If the dielectric slab is removed, then
 View Solution
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View Solution

