Four capacitors C1(=1μF),C2(=2μF),C3(=3μF) and C4(=4μF) are connected in a network as shown in the diagram. The emf of the battery is E=12V and its internal resistance is negligible. The keys S1 and S2 can be independetly put on or off. Indicate the charge on the capacitors by q1,q2,q3 and q4 respectively and the potential drops across them by V1,V2,V3 and V4 respectively.
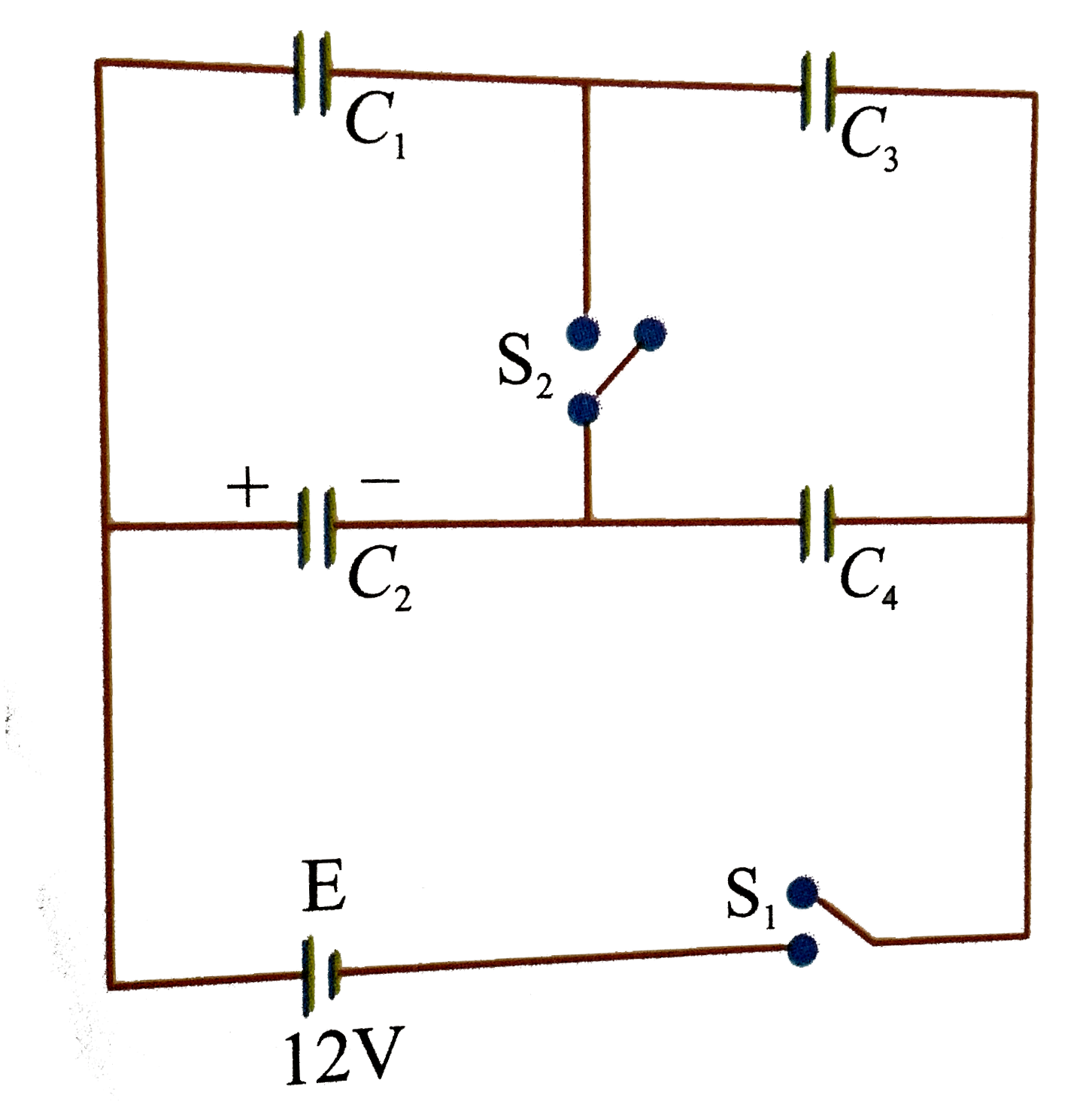
Initially key S2 is open. The key S1 is closed and teh capacitors are charged. If now key S2 be closed, the charge that will flow across this key is.
2.4μC
0.4μC
0.2μC
1.2μC
The correct Answer is:A
Before S2 is closed, C1 and C3 are in series and hence the total charge on their common plate is (+Q−Q)=0. Similarly for the plates joining C2 and C4. However when C2 and C4 is closed, the charges read just to the values calculated in problem 86. Hence total charge on the linking plates of C1 and C3 is (−8.4μC+10.8μC)=+2.4μC while the total charge on the linking plates of C2 and C4 is (−16.8μC+14.4μC=−2.4μC which shows that a charge of 2.4μC has crossed the key S2 from (C2,C4) to (C1,C3).
Topper's Solved these Questions
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Subjective
9 Videos
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Previous IIT-JEE
16 Videos
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-V
35 Videos
- ATOMS BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -4
47 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
Similar Questions
Four capacitors C1=8μF,
C2=2μf,C3=6μF, and C4=6,μF are arranged as shown in. Find the charge on all the capacitors in the circuit.
 .
.
View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .
.
View Solution
Knowledge Check
Four capacitors C1(=1μF),C2(=2μF),C3(=3μF) and C4(=4μF) are connected in a network as shown in the diagram. The emf of the battery is E=12V and its internal resistance is negligible. The keys S1 and S2 can be independetly put on or off. Indicate the charge on the capacitors by q1,q2,q3 and q4 respectively and the potential drops across them by V1,V2,V3 and V4 respectively.
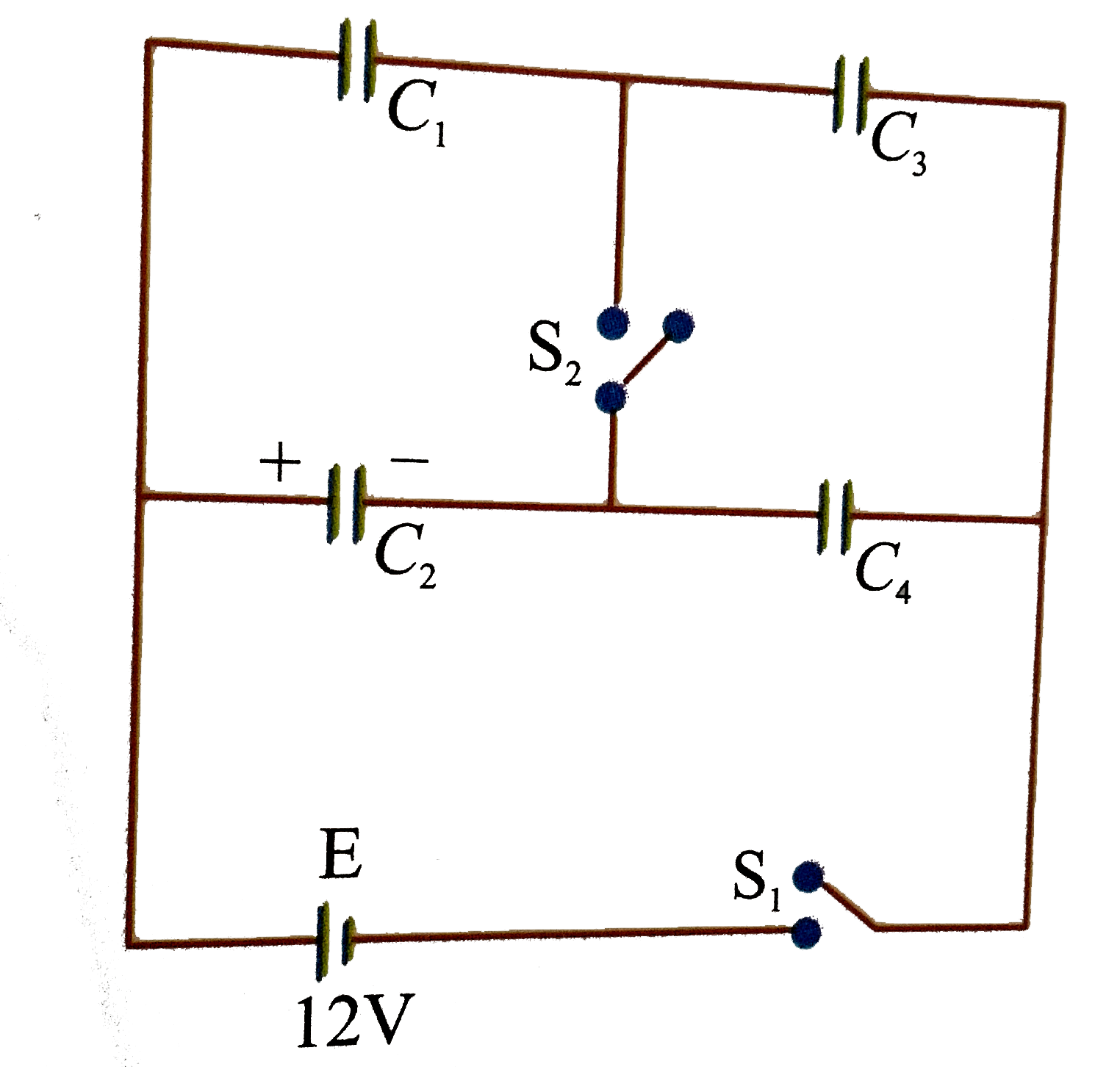
Initially key S2 is closed. Then the key S1 is now closed. Then the charges on the capacitors are.Aq1=q2=24μC,q3=q4=12μCBq1=q2=12μC,q3=q4=24μCCq1=10.8μC,q2=14.4μC,3q3=2q4,2q4=25.2μCD2q1=q2=16.8μC,4q3=3q4=43.3μCFour capacitors C1(=1μF),C2(=2μF),C3(=3μF) and C4(=4μF) are connected in a network as shown in the diagram. The emf of the battery is E=12V and its internal resistance is negligible. The keys S1 and S2 can be independetly put on or off. Indicate the charge on the capacitors by q1,q2,q3 and q4 respectively and the potential drops across them by V1,V2,V3 and V4 respectively.

Initially both the keys are open. Then the key S1 is closed. Then the charges on the capacitors are.Aq1=q2=16μC,q3=q4=9μCBq1=q3=16μC,q2=q4=9μCCq1=q4=9μC,q2=q3=16μCDq1=q3=9μC,q2=q4=16μCFour capacitors with capacitances C1=1μF,C2=1.5μF,C3=2.5μF and C4=0.5μF are connected as shown in Fig, to a 30 voltg source. The potentail difference between points a and b is
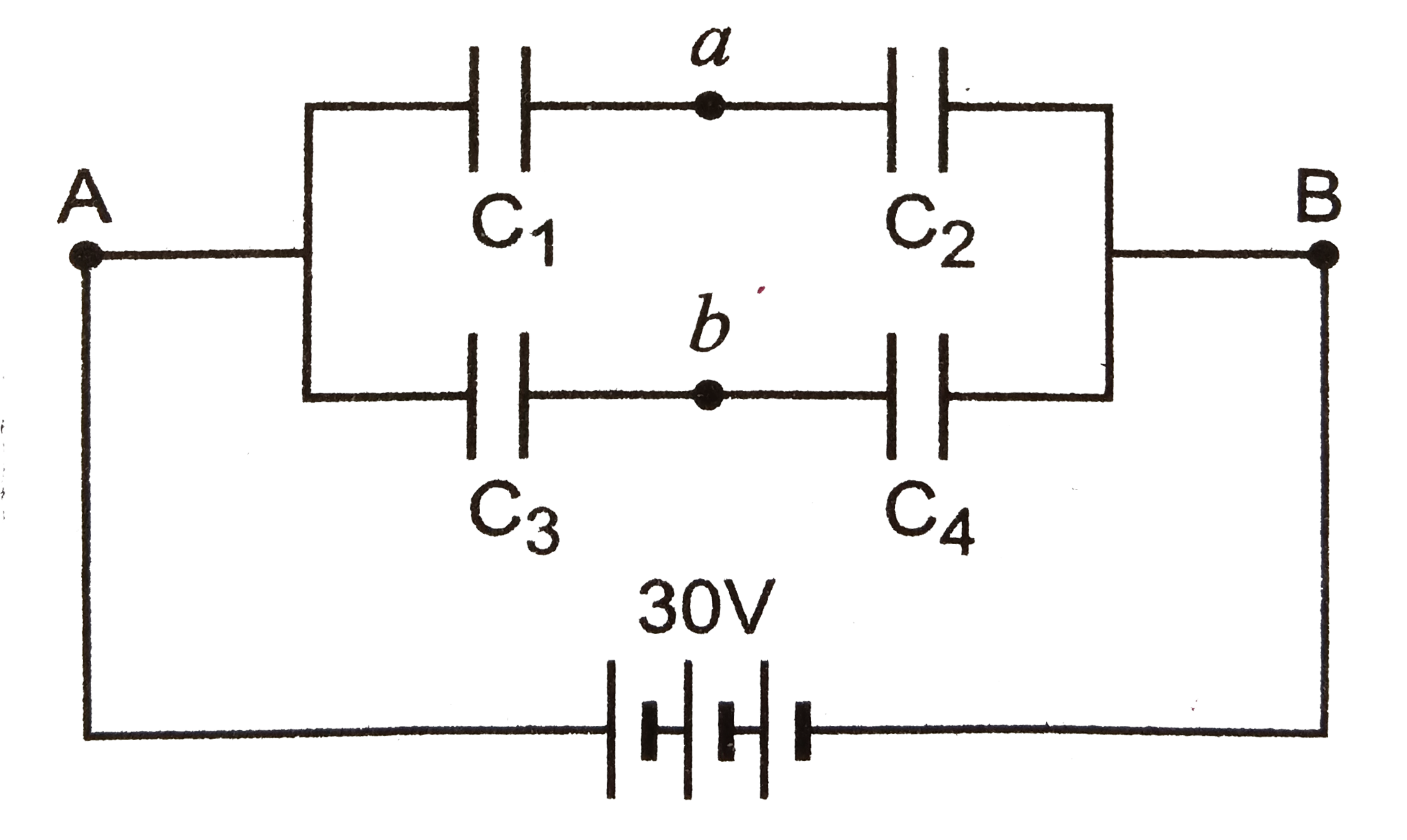 A5VB9VC10VD13V
A5VB9VC10VD13V
In the circuit shown the capacitors are C1=15μF,C2=10μFandC3=25μF. Find
the potential difference across each capacitor.
View SolutionFive capacitors of capacitances C1=C5=1μF,C2=C3=C4=2μF are connectes as shown in Fig. Calculate equivalent capacitance of the system between points A and B.
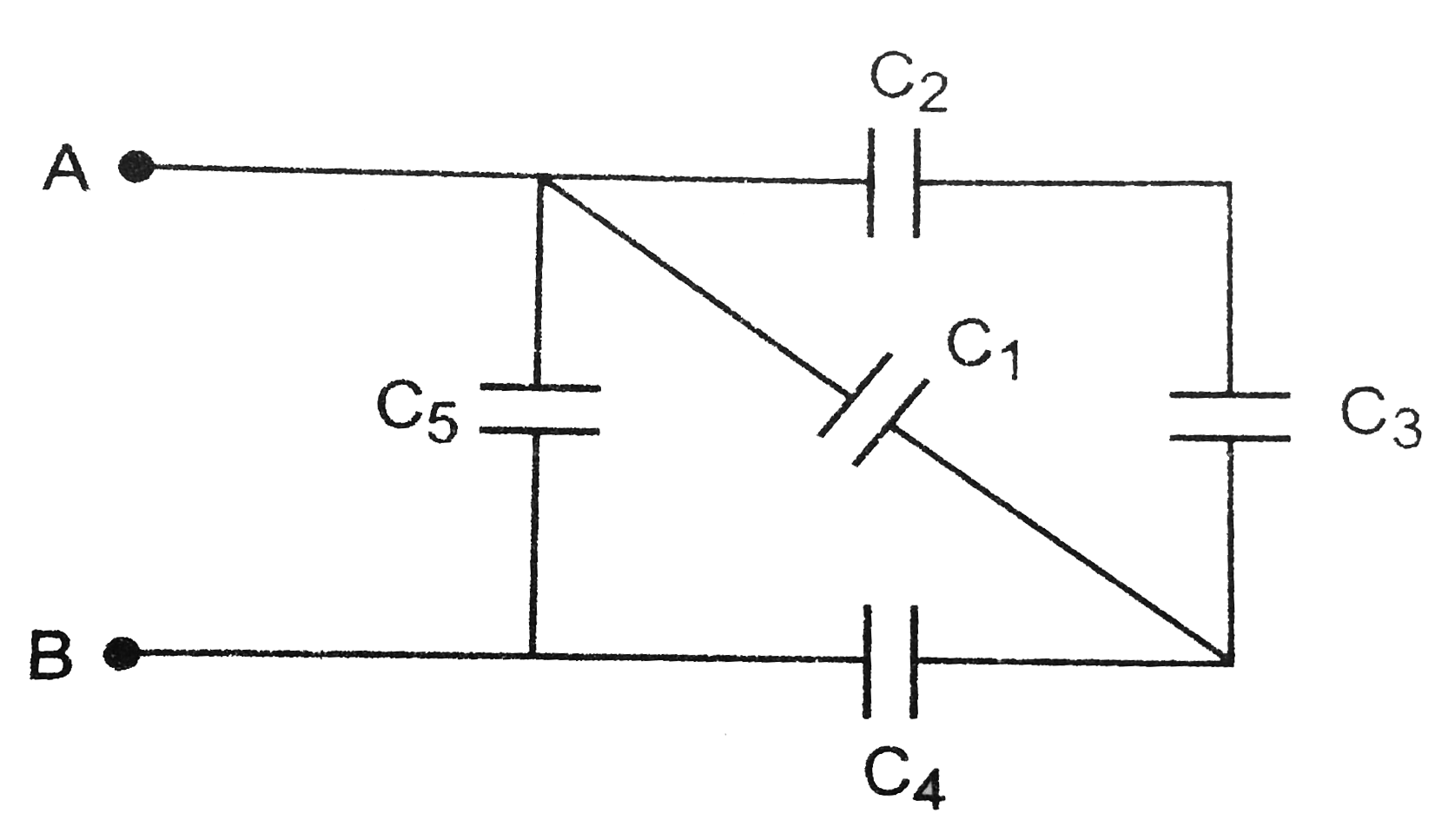
View SolutionIn the circuit shown the capacitors are C1=15μF,C2=10μFandC3=25μF. Find
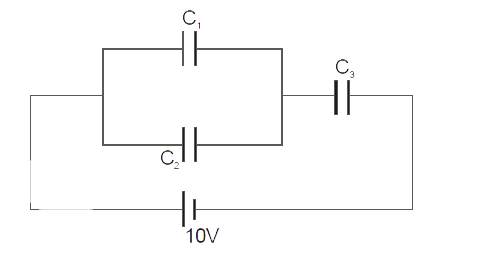
the charge on each capacitor and
View SolutionThree uncharged capacitors of capacities C1,C2 and C3 are connected as shown in the figure to one another and the potentials V1,V2 and V3 respectively. Then the potential at O will be
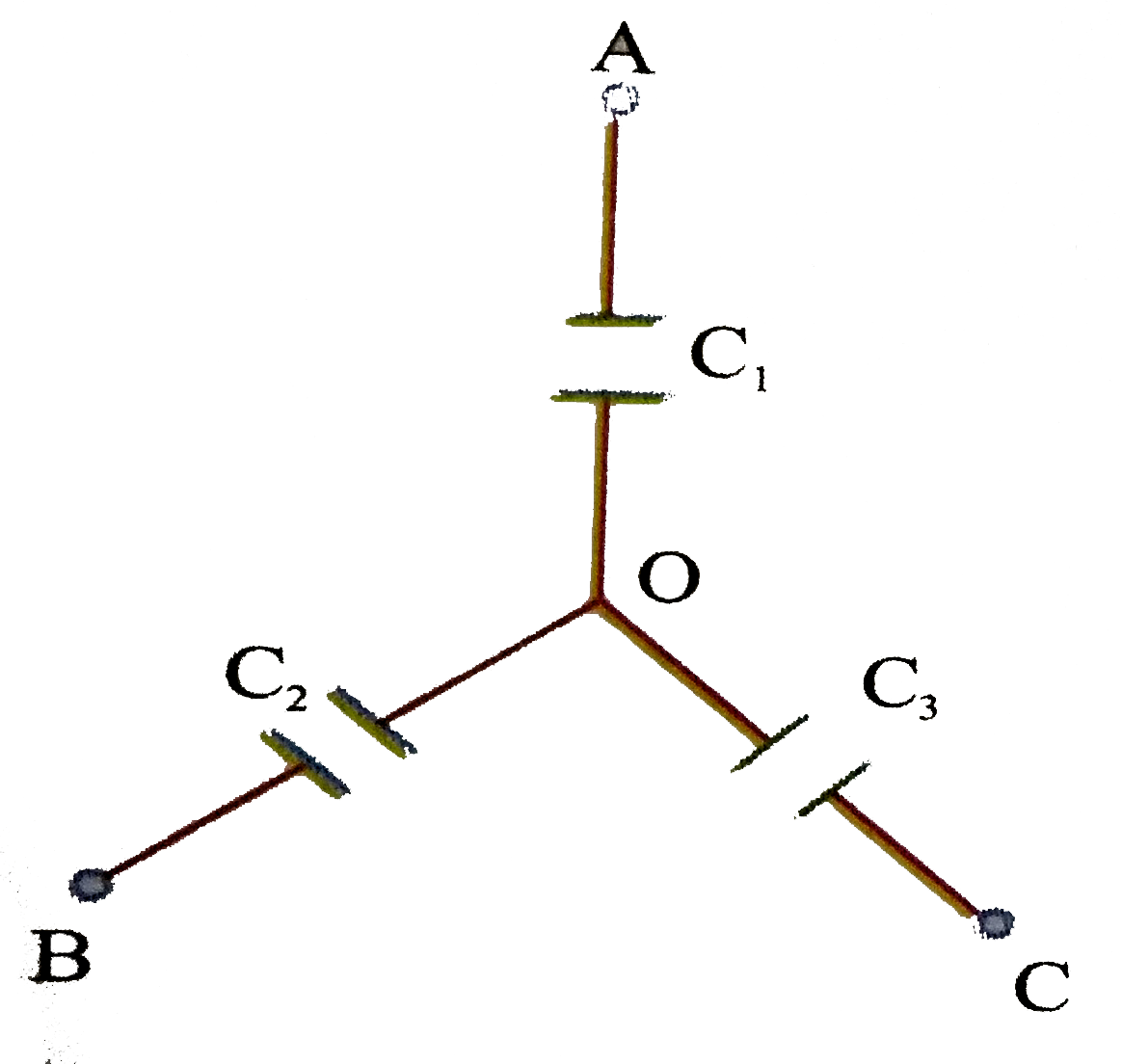 .
.
View Solutionif two capacitors of capacities C1=4μFandC2=1μF are connected in series, the ratio of the potential drops across the capacitors C1andC2 is
View Solution
