Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS The line XY cuts the line PR at Z Find the ratio PZ: ZR
Y→q+Y→S=λ5(λ+1)→q+45⋅1λ+1→s
Y=λ5(λ+1)
Y=45(λ+1)
λ=4
Y=425
Z=425−−→PR
ratio=21:4.
Similar Questions
Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS. The line XY cuts the line PR at Z. Then, PZ is
View SolutionIn the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.

View Solution
Knowledge Check
Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS. The line XY cuts the line PR at Z. Then, PZ is
A2125PRB1625PRC1725PRDnone of theseThe diagonals of a parallelogram PQRS are along the lines x+3y=4 and 6x-2y=7. Then PQRS must be a
ARectangleBSquareCCyclic QuadrilateralDRhombusThe diagonals of parallelogram PQRS are along the lines x+3y=4 and 6x−2y=7. Then PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombus
S and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
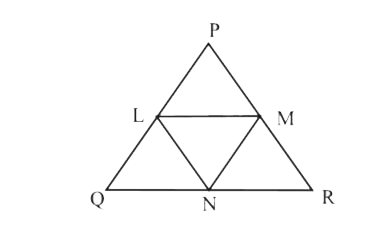
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View SolutionThe diagonals of a parallelogram PQRS are along the lines x+3y =4 and 6x-2y = 7, Then PQRS must be :
View SolutionThe diagonals of a parallelogram PQRS are along the lines x+3y =4 and 6x-2y = 7, Then PQRS must be :
View Solution
