A force Fy=(3x+2) N is acting on a body. The work done by this force if it tends to displace the body from x = 0 m to x = 4 m will be
32 J
16 J
0 J
(12x+8) J
The correct Answer is:C
To find the work done by the force Fy=(3x+2)N as it displaces a body from x=0m to x=4m, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a variable force can be calculated using the integral of the force over the distance moved:
W=∫x2x1F(x)dx
where F(x) is the force as a function of position x, and x1 and x2 are the initial and final positions, respectively.
Step 2: Set Up the Integral
In this case, the force is given by:
Fy=3x+2
We need to calculate the work done from x=0 to x=4:
W=∫40(3x+2)dx
Step 3: Calculate the Integral
Now, we can compute the integral:
W=∫40(3x+2)dx=∫403xdx+∫402dx
Calculating each part:
1. For ∫3xdx:
∫3xdx=3x22
Evaluating from 0 to 4:
(3(4)22)−(3(0)22)=3⋅162=24
2. For ∫2dx:
∫2dx=2x
Evaluating from 0 to 4:
(2(4))−(2(0))=8−0=8
Step 4: Combine the Results
Now, we can add the results of both integrals:
W=24+8=32J
Final Answer
The work done by the force as it displaces the body from x=0m to x=4m is:
32J
The work done W by a variable force can be calculated using the integral of the force over the distance moved:
W=∫x2x1F(x)dx
where F(x) is the force as a function of position x, and x1 and x2 are the initial and final positions, respectively.
In this case, the force is given by:
Fy=3x+2
We need to calculate the work done from x=0 to x=4:
W=∫40(3x+2)dx
Now, we can compute the integral:
W=∫40(3x+2)dx=∫403xdx+∫402dx
1. For ∫3xdx:
∫3xdx=3x22
Evaluating from 0 to 4:
(3(4)22)−(3(0)22)=3⋅162=24
∫2dx=2x
Evaluating from 0 to 4:
(2(4))−(2(0))=8−0=8
Now, we can add the results of both integrals:
W=24+8=32J
The work done by the force as it displaces the body from x=0m to x=4m is:
32J
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.4 Elastic and inelastic collision)23videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.5 Inertial and non-inertial frames)2videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.2 General idea of gravitational, electromagnetic and nuclear force from daily life experiences)3videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTRONS AND PHOTONSEXERCISE - Evaluation Test19videos
ELECTRONS AND PHOTONS
- BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)21videos
FRICTION IS SOLIDS AND LIQUIDS
Similar Questions
For the force displacement graph shown below. Calculate the work done by the force displacing the body from x=1 cm to x=5 cm.
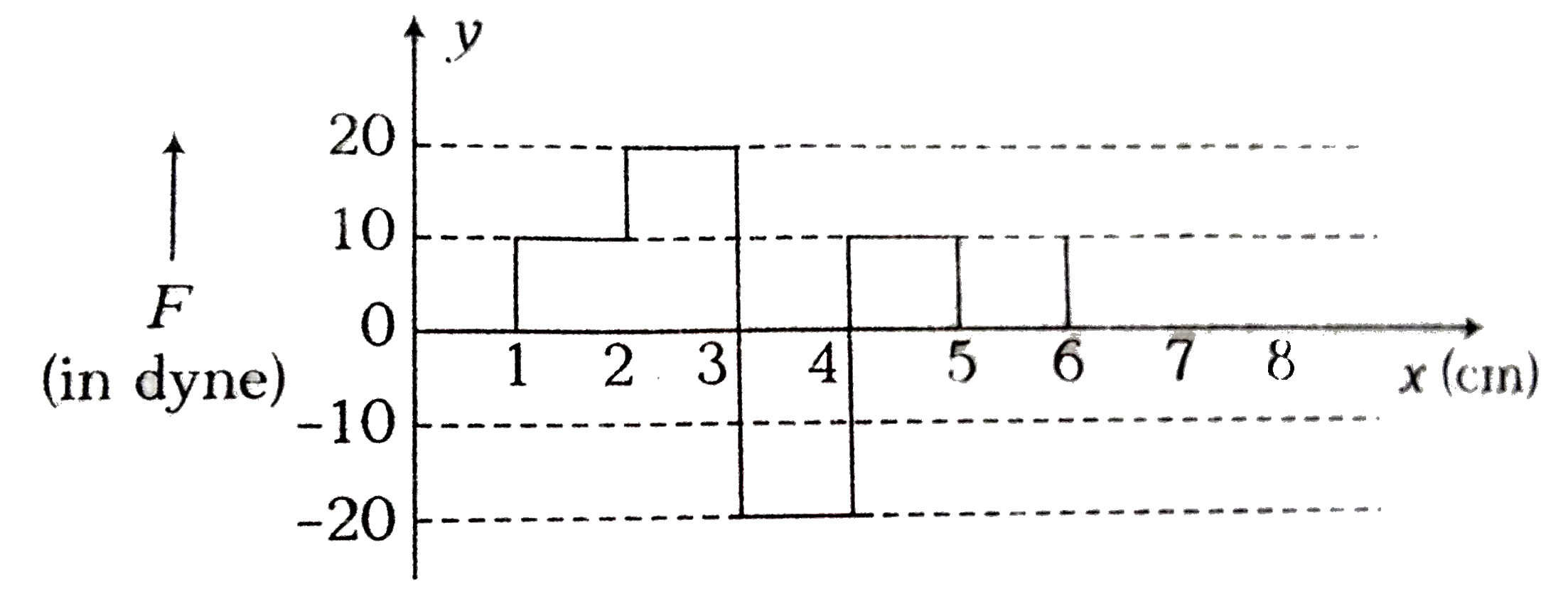 View Solution
View SolutionThe relationship between the force F and position x of body is as shown in figure. The work done in displacing the body from (x=1m to x=5m) will be
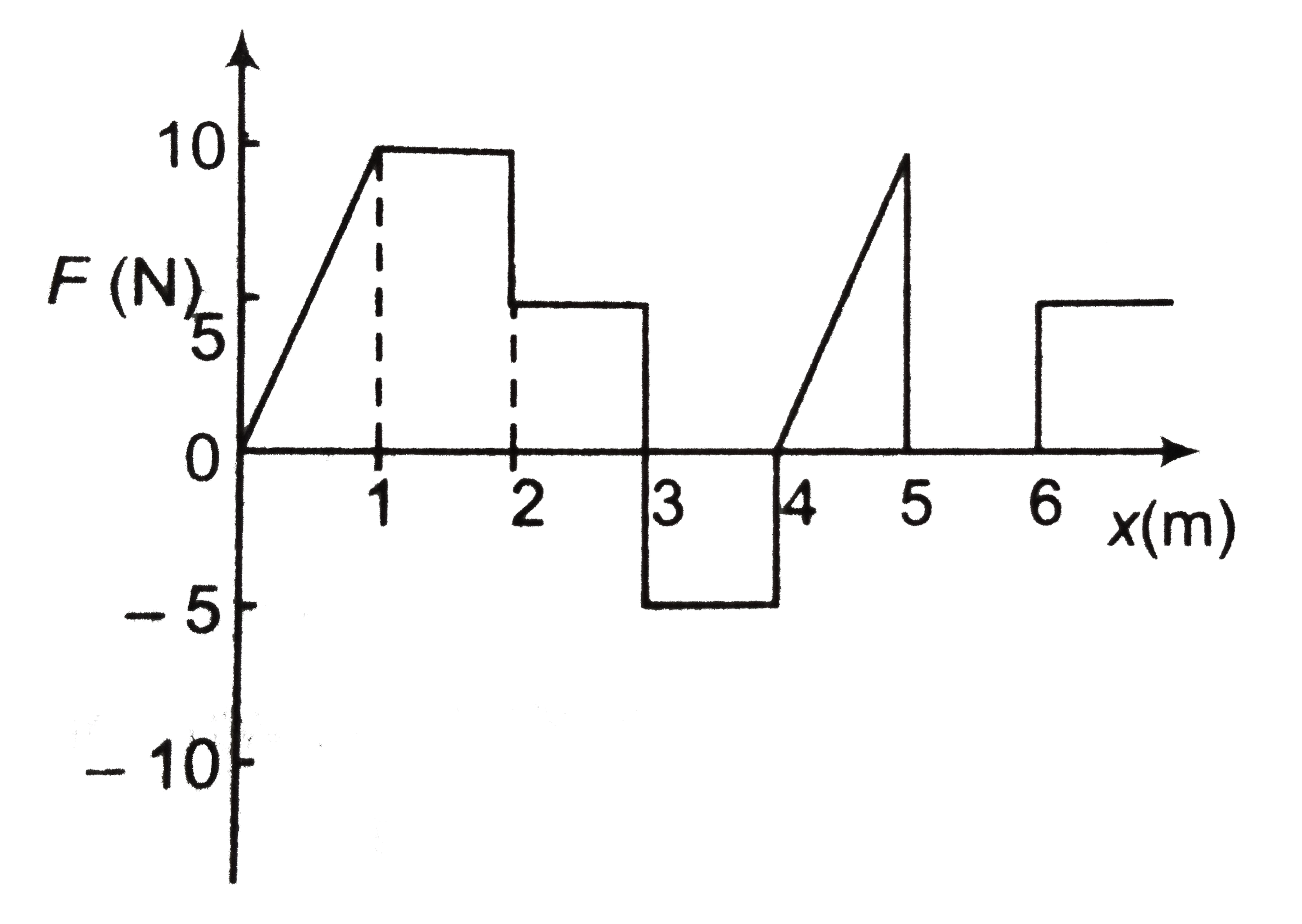 . View Solution
. View Solution
Knowledge Check
- Question 1 - Select One
A force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
A2.1JB2.5JC3.5JD4.5J - Question 2 - Select One
A force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
A(a) −10JB(b) 100JC(c) 10JD(d) 1J - Question 3 - Select One
A force →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle .Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m
A−10JB100JC10JD1J
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA block of mass 5kg initially at rest at the origin is acted upon by a force along the positive X−direction represented by
F=(20+5x)N. Calculate the work done by the force during the displacement of the block from x=0 to x=4m.View SolutionThe relationship between the force F and position x of a body is shown in figure the work done in displacing the body from x=1 m to x=5 m will be
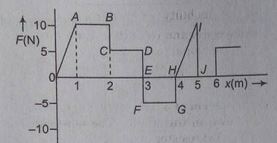 View Solution
View SolutionThe relationship between the force F and position x of a body is shown in figure the work done in displacing the body from x=1 m to x=5 m will be
 View Solution
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View Solution

