The work done an a particle of mass m by a force
K⎡⎢
⎢⎣x(x2+y2)3/2ˆi+y(x2+y23/2)ˆj⎤⎥
⎥⎦<br>(Kbe∈gaconstantofap∝riatedimensions),whentheparticalistakenomthep∮(a,0)→thep∮(0,a) along a circular path of radius a about the origin in x - y plane is
2Kπa
Kπa
Kπ2a
0
The correct Answer is:D
Step by step video, text & image solution for The work done an a particle of mass m by a force K[(x)/((x^(2) + y^(2))^(3//2)) hati +(y)/((x^(2) + y^(2^(3//2))) hatj)] (K being a constant of appropriate dimensions), when the partical is taken from the point (a,0) to the point (0,a) along a circular path of radius a about the origin in x - y plane is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.4 Elastic and inelastic collision)23videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.5 Inertial and non-inertial frames)2videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - FORCE EXERCISE - Competitive Theinking (4.2 General idea of gravitational, electromagnetic and nuclear force from daily life experiences)3videos
FORCE
- BOOK - TARGET PUBLICATIONCHAPTER - ELECTRONS AND PHOTONSEXERCISE - Evaluation Test19videos
ELECTRONS AND PHOTONS
- BOOK - TARGET PUBLICATIONCHAPTER - FRICTION IS SOLIDS AND LIQUIDS EXERCISE - MCQ (EVALUATION TEST)21videos
FRICTION IS SOLIDS AND LIQUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum distance of the point (a, 0) from the curve 2x2+y2−2x=0 is -
A√1+2k−k2B√1−2k+2k2C√1+2k+2k2D√1−2k+k2 - Question 2 - Select One
A force F=−K(yˆI+xˆj)(whereKisaposiveconstant)actsonapartic≤mov∈g∈thexypla≠.Start∈gformtheorig∈al,theparticalistakenalong∈thepositivexaξs→thep∮(x,0)andthenpartical→theyaξsthep∮(x,0).The→talworkdo≠bytheforceF on the particls is
A−2Ka2B2Ka2C−Ka2DKa2 - Question 3 - Select One
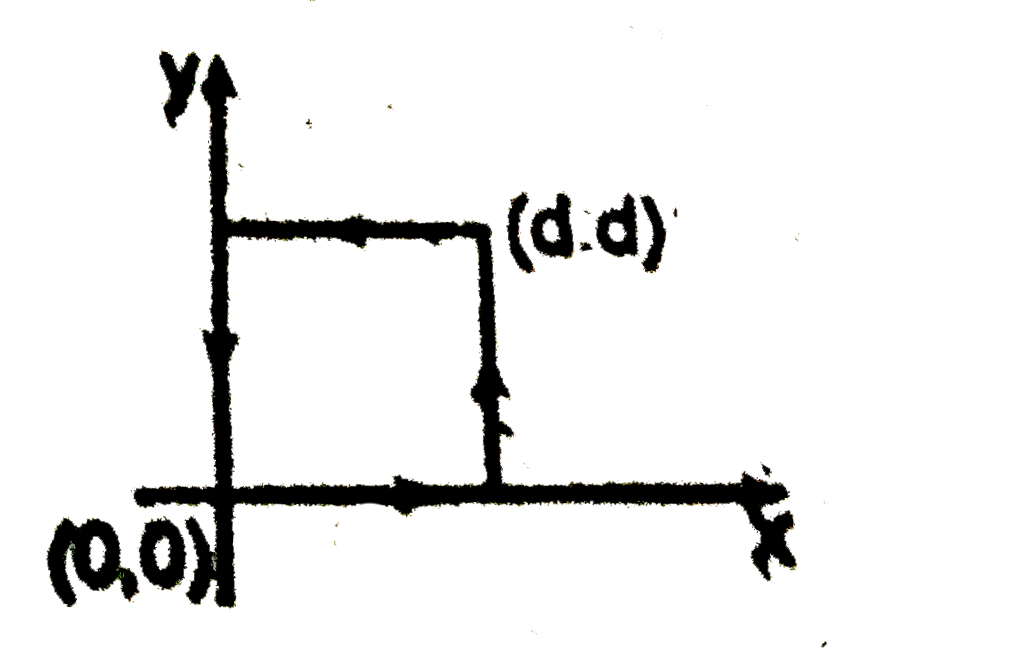
A force F=−K(yˆi+xˆj), acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0) and then parallel to the y-axis to the point (a, a). The total work done by the force is
A−2Ka2B2Ka2C−Ka2DKa2
If the image of the point (1,2,3) in the plane x+2y=0 is (h,k,l)then l=
View SolutionThe maximum distance of the point (k,0) from the curve 2x2+y2−2x=0 is equal to
View SolutionThe distance of a point (2,3) from the line 2x -3y + 9 = 0 measured along a line x-y +1 =0 is :
View SolutionLocus of image of the point (2,3) in the line (2x−3y+4)+k(x−2y+3)=0,k in R is
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
 View Solution
View Solution

