A horizontal uniform glass tube of 100cm length is sealed at both ends contains 10cm mercury column in the middle , the temperature and pressure of air on either side of mercury column are repectively 31∘C and 76cm of mercury, if the air column at one end is kept at0∘C and the other end at 273∘C then pressure if air which is 0∘C is
(in cm of Hg)
76
88.2
102.4
122
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Setup
We have a horizontal glass tube of length 100 cm, sealed at both ends, containing a 10 cm mercury column in the middle. The air pressure on either side of the mercury column is 76 cm of mercury at a temperature of 31°C.
Step 2: Define the Lengths
Since the total length of the tube is 100 cm and there is a 10 cm mercury column in the middle, the lengths of the air columns on either side of the mercury column are:
- Length of air column on the left (L1) = 45 cm
- Length of air column on the right (L2) = 45 cm
Step 3: Identify the New Conditions
One end of the tube is kept at 0°C and the other at 273°C. This means:
- Temperature on the left side (T1) = 0°C = 273 K
- Temperature on the right side (T2) = 273°C = 546 K
Step 4: Apply the Gas Law
Using the ideal gas law for both sides of the mercury column, we can set up the following relationship based on the fact that the number of moles of air remains constant:
P1⋅L1T1=P2⋅L2T2
Where:
- P1 = pressure of air at 0°C (to be found)
- P2 = pressure of air at 273°C = 76 cm of mercury
- L1 = length of air column at 0°C = 45−x
- L2 = length of air column at 273°C = 45+x
Step 5: Determine the Shift of Mercury Column
Since the mercury column shifts due to the temperature difference, let x be the distance the mercury column moves towards the cooler side (0°C). Thus:
- New length on the left (L1) = 45−x
- New length on the right (L2) = 45+x
Step 6: Set Up the Equation
From the gas law, we have:
P1(45−x)273=76(45+x)546
Step 7: Solve for x
Cross-multiplying gives:
P1(45−x)⋅546=76(45+x)⋅273
Step 8: Simplify the Equation
Since the pressures are equal, we can simplify and solve for x:
P1(45−x)=76⋅273546(45+x)
Step 9: Calculate x
After solving the above equation, we find x=15 cm.
Step 10: Calculate the Pressure P1
Now substituting x back into the equation to find P1:
P1⋅(45−15)=76⋅273546⋅(45+15)
P1⋅30=76⋅273546⋅60
P1=76⋅273⋅30546⋅60
Calculating this gives:
P1=102.3 cm of Hg
Final Answer
The pressure of air at 0°C is approximately 102.3 cm of Hg.
---
We have a horizontal glass tube of length 100 cm, sealed at both ends, containing a 10 cm mercury column in the middle. The air pressure on either side of the mercury column is 76 cm of mercury at a temperature of 31°C.
Since the total length of the tube is 100 cm and there is a 10 cm mercury column in the middle, the lengths of the air columns on either side of the mercury column are:
- Length of air column on the left (L1) = 45 cm
- Length of air column on the right (L2) = 45 cm
One end of the tube is kept at 0°C and the other at 273°C. This means:
- Temperature on the left side (T1) = 0°C = 273 K
- Temperature on the right side (T2) = 273°C = 546 K
Using the ideal gas law for both sides of the mercury column, we can set up the following relationship based on the fact that the number of moles of air remains constant:
- P1 = pressure of air at 0°C (to be found)
- P2 = pressure of air at 273°C = 76 cm of mercury
- L1 = length of air column at 0°C = 45−x
- L2 = length of air column at 273°C = 45+x
Since the mercury column shifts due to the temperature difference, let x be the distance the mercury column moves towards the cooler side (0°C). Thus:
- New length on the left (L1) = 45−x
- New length on the right (L2) = 45+x
From the gas law, we have:
P1(45−x)273=76(45+x)546
Cross-multiplying gives:
P1(45−x)⋅546=76(45+x)⋅273
Since the pressures are equal, we can simplify and solve for x:
P1(45−x)=76⋅273546(45+x)
After solving the above equation, we find x=15 cm.
Now substituting x back into the equation to find P1:
P1⋅(45−15)=76⋅273546⋅(45+15)
P1⋅30=76⋅273546⋅60
P1=76⋅273⋅30546⋅60
Calculating this gives:
P1=102.3 cm of Hg
The pressure of air at 0°C is approximately 102.3 cm of Hg.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-I (C.W.)
23 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL-II (C.W.)
27 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Examples
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV
39 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
Similar Questions
The temperature and pressure at Simla are 15.0∘C and 72.0cm of mercury and at Kalka these are 35.0∘C and 76.0 cm of mercury. Find the ratio of air density at Kalka to the air density at Simla.
View SolutionA long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at 0∘C. Find the length of the mercury thread, as read on this scale, at 100∘C.
View Solution
Knowledge Check
A small capillry tube of length 100cm closed at one end is kept horizontally and a mercury column of length 10cm is exactly in the middle. If the atmospheric pressure is 1 atm then identify the correct option(s).
AThe pressure of "air trapped" in the orgina: horizontal position is 750mm of Hg.BThe length of the air trapped when the tube is held vertically with open end upwards is 45×7686cm.CThe length of the air trapped when the tube is held vertically with open end downwards is 45×7666cm.DNo air will be trapped when it is held vertically with open end downward.The height of mercury which exerts the same pressure as 20 cm of water column, is
A1.47 cmB14.8cmC148 cmDNone of these
A vertical uniform U tube open at both ends contains mercury. Water is poured in one limb until the level of mercury is depressed 2cm in that limb. What is the length of water column when this happens.
View SolutionA glass tube sealed at both ends is 100cm long, It lies horizontally with the middle 10cm containing mercury. The two ends of the tube contain air at 27∘Cand at a pressure 76cm of mercury. The air column on one side is maintained at 0∘Cand the other side is maintained at 127∘C. Calculate the length of the air column on the cooler side. neglect the changes in the volume of mercury and of the glass.
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
View SolutionA horizontal tube of 1m is closed at both ends. A mercury column of 20 cm is contained in the middle of the tube and two equal lengths of this tube contain air at an atmospheric pressure of 76cm. The tube is now placed vertically. Calculate the distance through which the mercury column will be displaced at a constant temperature.
View SolutionA narrow uniform glass tube 80 cm long and open at both ends is half immersed in mercurry. Then the top of the tube is closed and it is taken out of mercury. A column of mercury 22 cm long then remains in the tube. What is the atmospheric pressure?
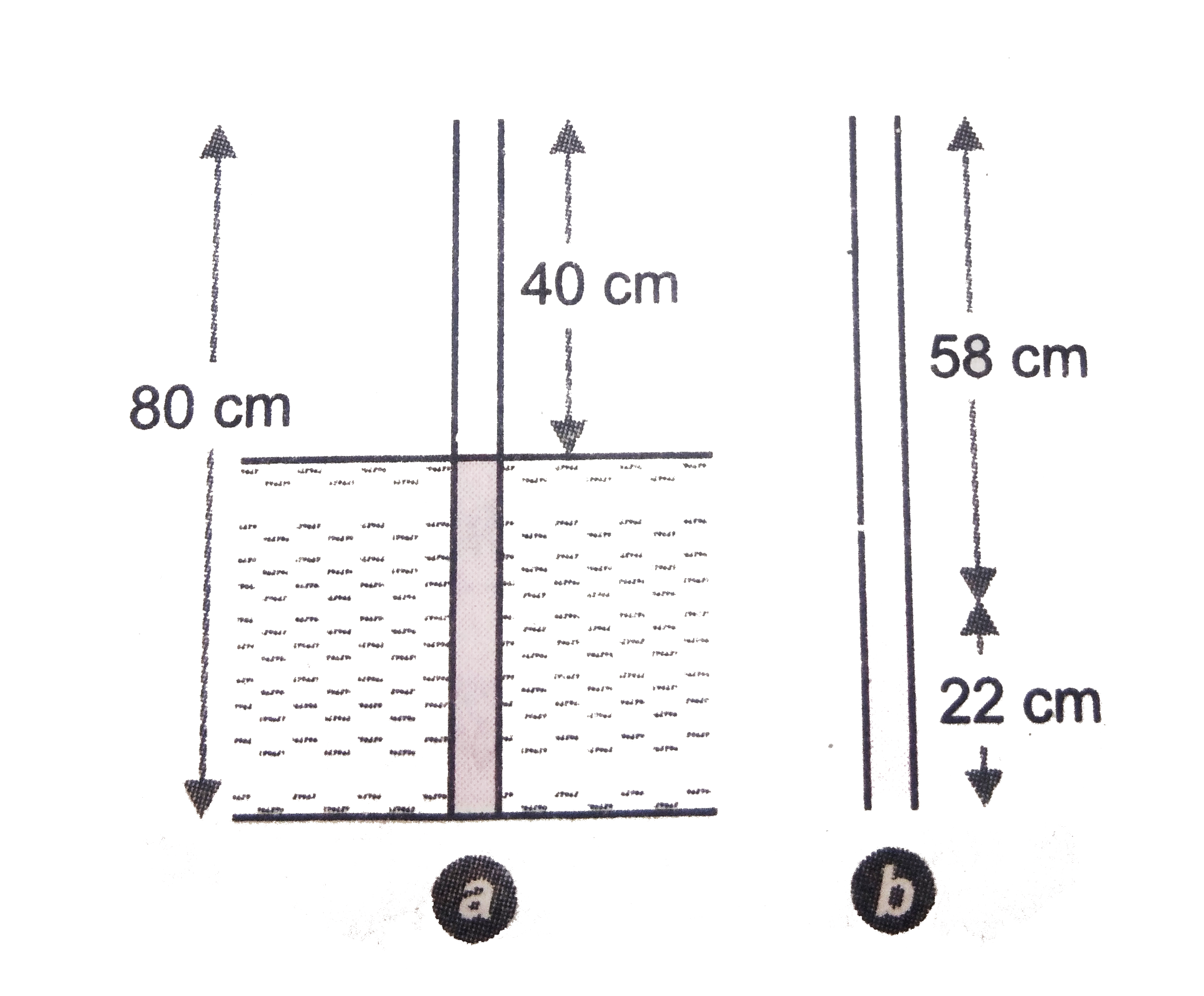
View SolutionIn the given figure a glass tube lies horizontally with the middle 20cm containing mercury. The two ends of the tube contains air at 27∘C and at a pressure 76cm of mercuy. Now the air column on one side in maintained at 0∘C and the other side is maintained at 127∘C. Find the new length of the air column on the cooler side. Neglect the changes in the volume of mercury and of the glass.

View Solution
