In the system shown in Fig, a disc pivoted at its centre has a spring attached at a distance 'a' form centre and a mass 'm' that cen rotate the disc. For small angular displacement calculate the frequency of oscillation
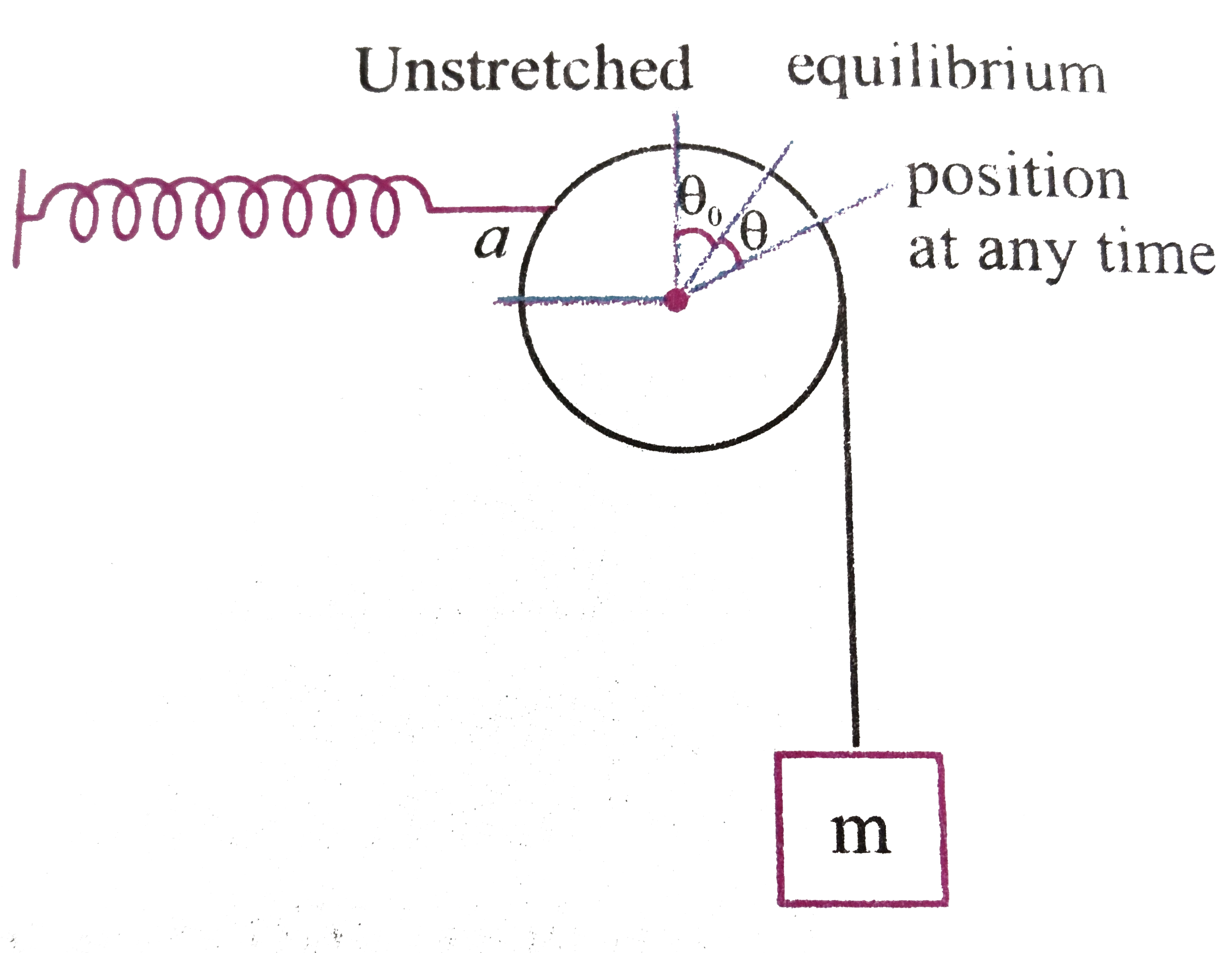
In the equilibrium position stretch of spring is x0=aθ0. Torque fo spring force and weight balance each other,
i.e., Ka2θ0=mgr…..(i)
In a slightly displacement position equations of motion are mg−T=ma=mrα....(ii)
and Tr−Ka2(θ0+θ)=Tα....(iii)
Substituting the value of T from Eqn.(ii) into Eqn. (iii), we get
m(g−rα)r−Ka2(θ0+θ)=Iα
or α=−ka2(I+mr2)θ
Compering above Eqn. with necessary consition of SHM, i.e.,
α=−ω2θ,ω=√Ka2I+mr2
and f=12√Ka2I+mr2
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions

A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionWhat will be distance of centre of mass of the disc (See fig.) from its geometrical centre ?
View Solution
Knowledge Check
A small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmA small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmOne end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?
 AaB2aCa/2Dnone of these
AaB2aCa/2Dnone of these
A disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.

View SolutionWhat is the gravitational potential energy of a particle of mass m kept at a distance x from the centre of a disc of mass M on its axis ? The radius of the disc is R.
View SolutionOne end of a metal rod of length L and mass M is pivoted to a fixed support and to its free end, a thin disc of mass m and radius r (L) is attached at its centre. In one case, the disc is attached to the rod in such a way that it is not free to rotate about its centre and in another case, teh disc is free to rotate about its centre. When the rod-disc system is displaced slightly from its equilibrium position and released. it peforms S.H.M. in vertical plane. Compare the restoring torque acting on the system and angular frequency in both the cases.
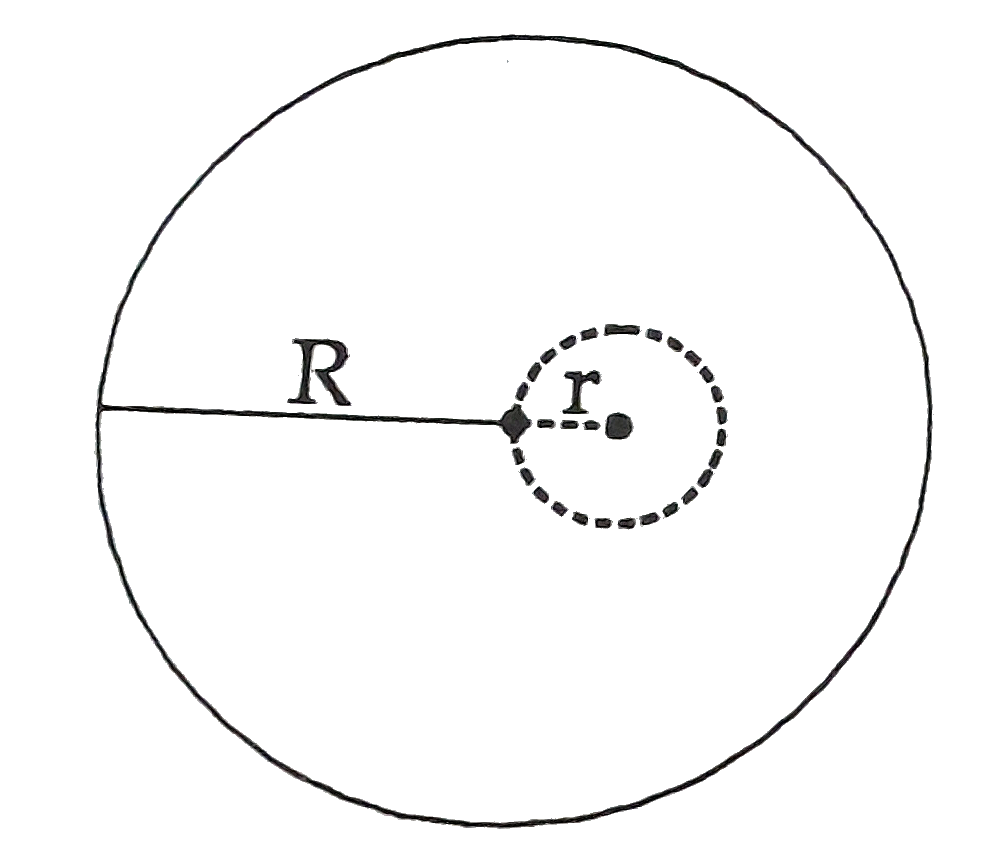
View SolutionA uniform disc (of mass M and radius a) has a hole (of radius b) drilled through it. The centre of the hole is at a distance c from the centre of the original disc. What is the moment of inertia of the disc about an axis through the centre of the disc and perpendicular to its plane ?
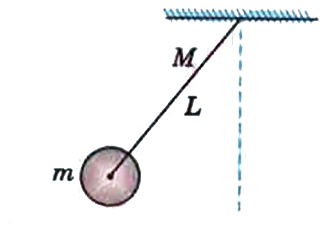
View SolutionA body of mass m, is attached to a vertical rod of mass M nad length L, hung from a pivoted supprot. A springs of constant K fixed to a support on the left as shown and is attached to the rod at a distance form the pivot. The frequency of the oscillation is:
View Solution