A spring has length l and force constant k it is cut into two springs of legnth l1 and l2 such that l1=nl2(n=an integer). Mass 'm' suspended form l1 oscillates with time period.
T=2π√m(n+1)K
T=2π√nm(n+1)K
T=2π√mK
T=2π√(n+1)mK
The correct Answer is:B
K1=(l1+l2l1)K,T=2π√mK1
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)
36 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -III
51 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A simple spring has length l and force constant K. It is cut into two springs of lengths l1andl2 such that l1=nl2 (n = an integer). The force constant of spring of length l1 is
View SolutionA spring of force constant k is cut into two pieces of lengths l1 and l2. Calculate force constant of each part.
View Solution
Knowledge Check
A spring has length'l' and spring constant 'k'. It is cut into two pieces of lengths l1andl2 such that l1=nl2. The force constant of the spring of length l1 is
Ak(l+n)BkCk(n+1)Dk(n+l)nA uniform spring whose unstressed length is l has a force constant k. The spring is cut into two pieces of unstressed lengths l1 and l2 where l1=nl2 where n being on integer. Now a mass m is made to oscillate with first spring. The time period of its oscillation would be
AT=2π√mnk(n+1)BT=2π√mk(n+1)CT=2π√mkDT=2π√m(n+1)nkA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
Al2l1B2l2l1Cl1l2DNone
A uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k? what is the ratio k1/k2
View SolutionA spring of stiffness constant k and natural length l is cut into two parts of length 3l/4andl/4, respectively, and an arrangement is made as shown in figure . If the mass is slightly displaced , find the time period of oscillation.
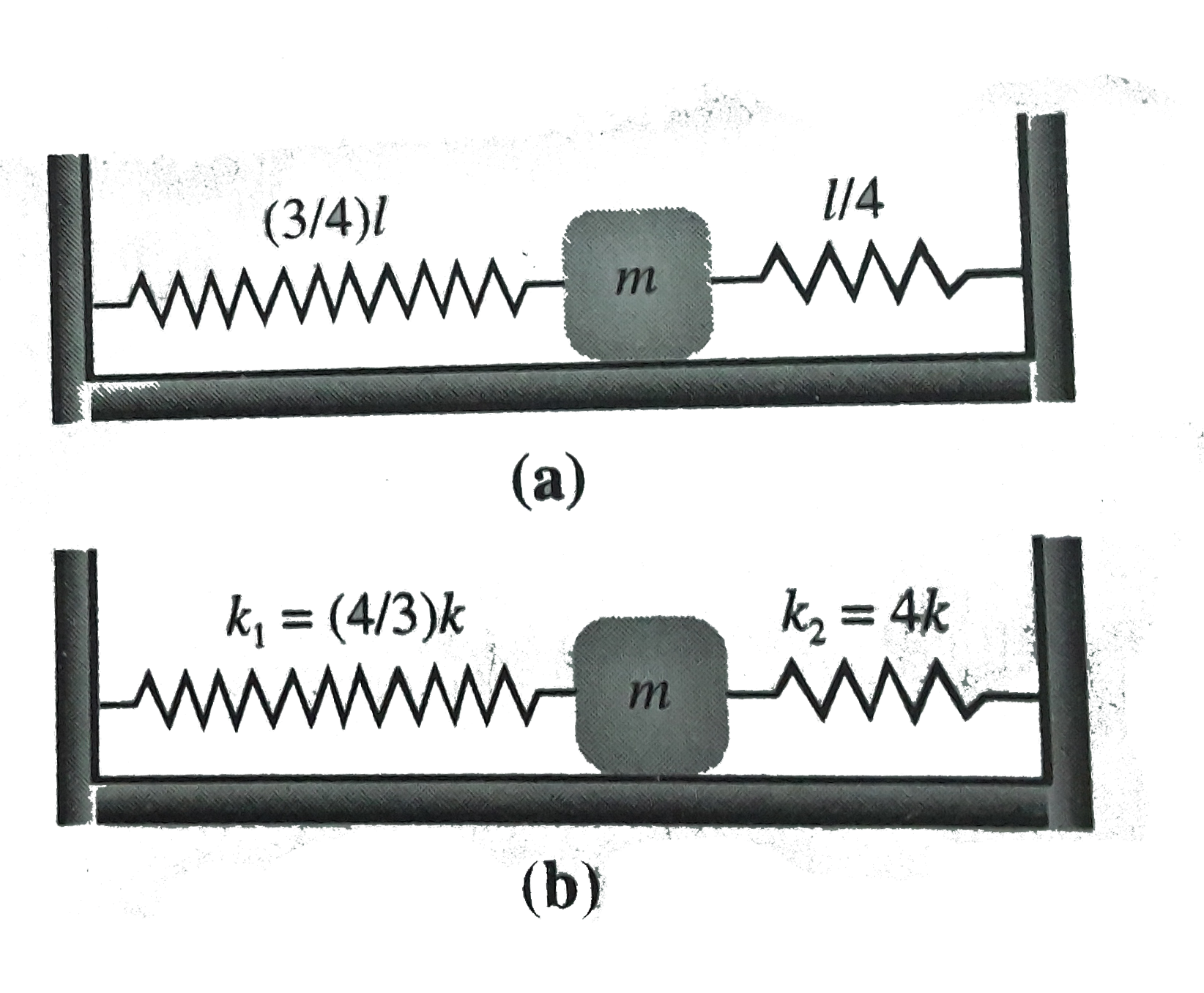
View SolutionA mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is f1. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is f2 . Which of the following relations between the frequencies is correct
View SolutionA spring of force constant k is cut into two parts whose lengths are in the ratio 1:2. The two parts are now connected in parallel and a block of mass m is suspended at the end of the combined spring. The period of oscillation of block is
View SolutionA spring has a force constant k and a mass m is suspended from it the spring is cut in two equal halves and the same mass is suspended from one of the halves. If the frequency of oscillation in the first case is n, then the frequency in the second case will be
View Solution