In a spring block system if length of the spring is reduced by 1%, then time period
increase by 2%
increase by 0.5%
decrease by 2%
decrease by 0.5%
The correct Answer is:D
To solve the problem of how the time period of a spring block system changes when the length of the spring is reduced by 1%, we can follow these steps:
Step 1: Understand the relationship between time period and spring constant
The time period T of a spring block system is given by the formula:
T=2π√mk
where m is the mass and k is the spring constant.
Step 2: Determine the effect of spring length on spring constant
The spring constant k is inversely proportional to the length of the spring l. This means:
k∝1l
If the length l decreases, the spring constant k increases.
Step 3: Calculate the change in length
Given that the length of the spring is reduced by 1%, we can express this mathematically as:
dll=−0.01
This indicates that the length is decreasing.
Step 4: Relate the change in spring constant to the change in length
Since k is inversely proportional to l, we can express the change in k as:
dkk=−dll
Substituting the value of dll:
dkk=0.01
This indicates that k increases by 1%.
Step 5: Differentiate the time period formula
To find the change in the time period T, we differentiate the time period equation:
dT=ddk(2π√mk)
Using the chain rule, we find:
dT=−πmk3/2dk
Step 6: Relate the change in time period to the change in spring constant
Now, we can express the relative change in time period:
dTT=−12dkk
Step 7: Substitute the change in spring constant into the time period equation
Substituting dkk=0.01:
dTT=−12×0.01=−0.005
Step 8: Convert to percentage change
To find the percentage change in time period:
dTT×100=−0.5%
This indicates that if the length of the spring decreases by 1%, the time period decreases by 0.5%.
Final Answer
If the length of the spring is reduced by 1%, then the time period decreases by 0.5%.
---
The time period T of a spring block system is given by the formula:
T=2π√mk
where m is the mass and k is the spring constant.
The spring constant k is inversely proportional to the length of the spring l. This means:
k∝1l
If the length l decreases, the spring constant k increases.
Given that the length of the spring is reduced by 1%, we can express this mathematically as:
dll=−0.01
This indicates that the length is decreasing.
Since k is inversely proportional to l, we can express the change in k as:
dkk=−dll
Substituting the value of dll:
dkk=0.01
This indicates that k increases by 1%.
To find the change in the time period T, we differentiate the time period equation:
dT=ddk(2π√mk)
Using the chain rule, we find:
dT=−πmk3/2dk
Now, we can express the relative change in time period:
dTT=−12dkk
Substituting dkk=0.01:
dTT=−12×0.01=−0.005
To find the percentage change in time period:
dTT×100=−0.5%
This indicates that if the length of the spring decreases by 1%, the time period decreases by 0.5%.
If the length of the spring is reduced by 1%, then the time period decreases by 0.5%.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -II (C.W)
36 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -III
51 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Knowledge Check
In a spring block system if length of the spring is increased by 4%, then time period
Aincrease by 2%Bincrease by 0.5%Cdecrease by 2%Ddecrease by 0.5%Assertion : Time period of a spring-block is T. If length of spring is decreased, time period will decrease.
Reason If length is decreased, then the block will have to travel less distance and it will take less time.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.The time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
AT=t1+t2BT2=t21+t22CT−1=t−11+t−12DT−2=t−21+t−22
A spring-block system is executing SHM. The mass of the block is M and the time period of oscillation is T. If the mass of the block is increased by m, then time period becomes 7T4. Now, find the ratio of mM ,
View SolutionThe length of a simple pendulum is increased by 1%. Its time period will
View SolutionWhat will be the spring constant k of a. spring if length of the spring is made n times?
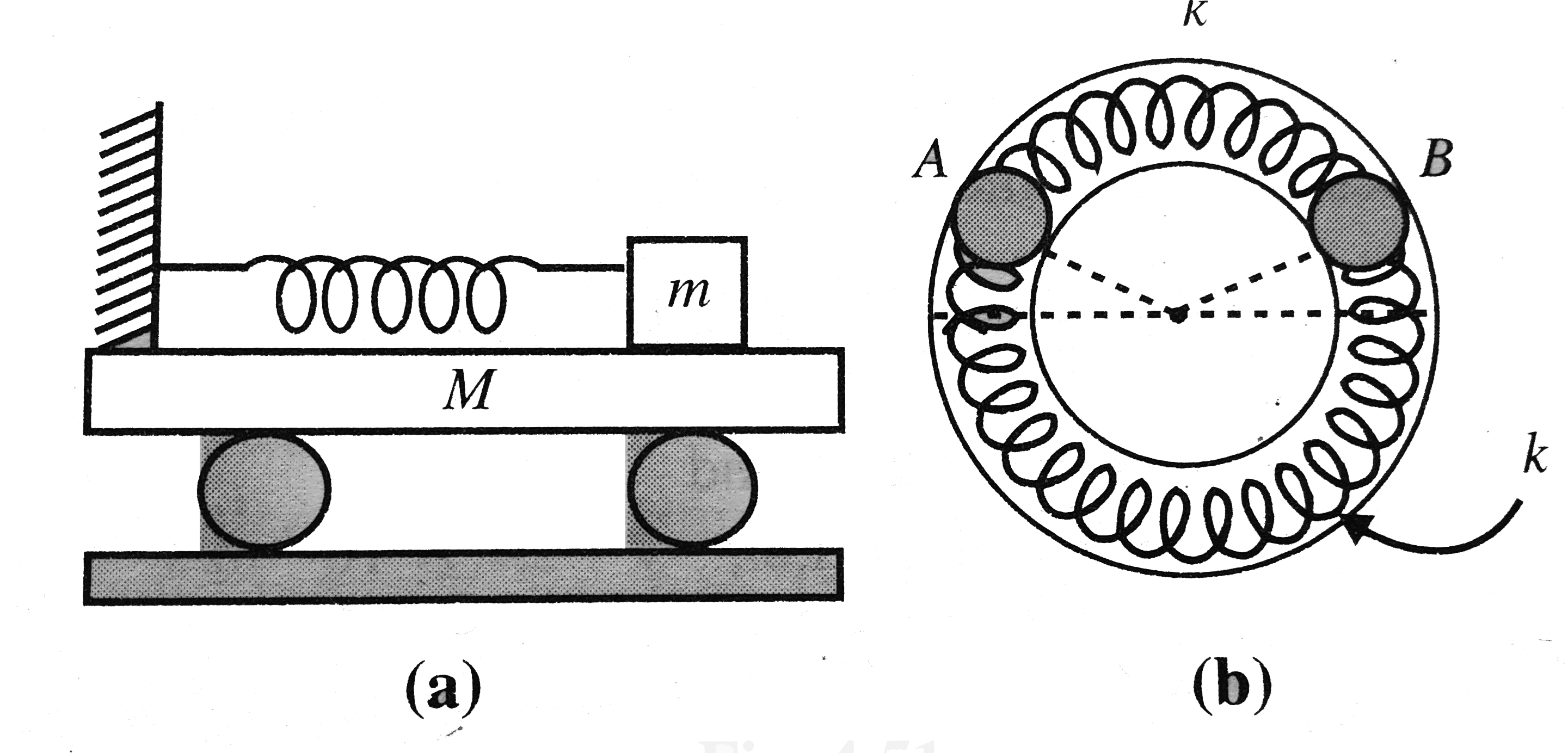
View Solutionfigure (a) and (b) represent spring- block system. If m is displacement slightly , find the time period of oscillation of the system.
View SolutionStatement-I : Time period of spring block system is the same whether in an accelerated or in an inertial frame of reference.
Statement-II : Mass of the block of spring block system and spring constant of the spring are independent of the acceleration of the frame of reference.
View Solution