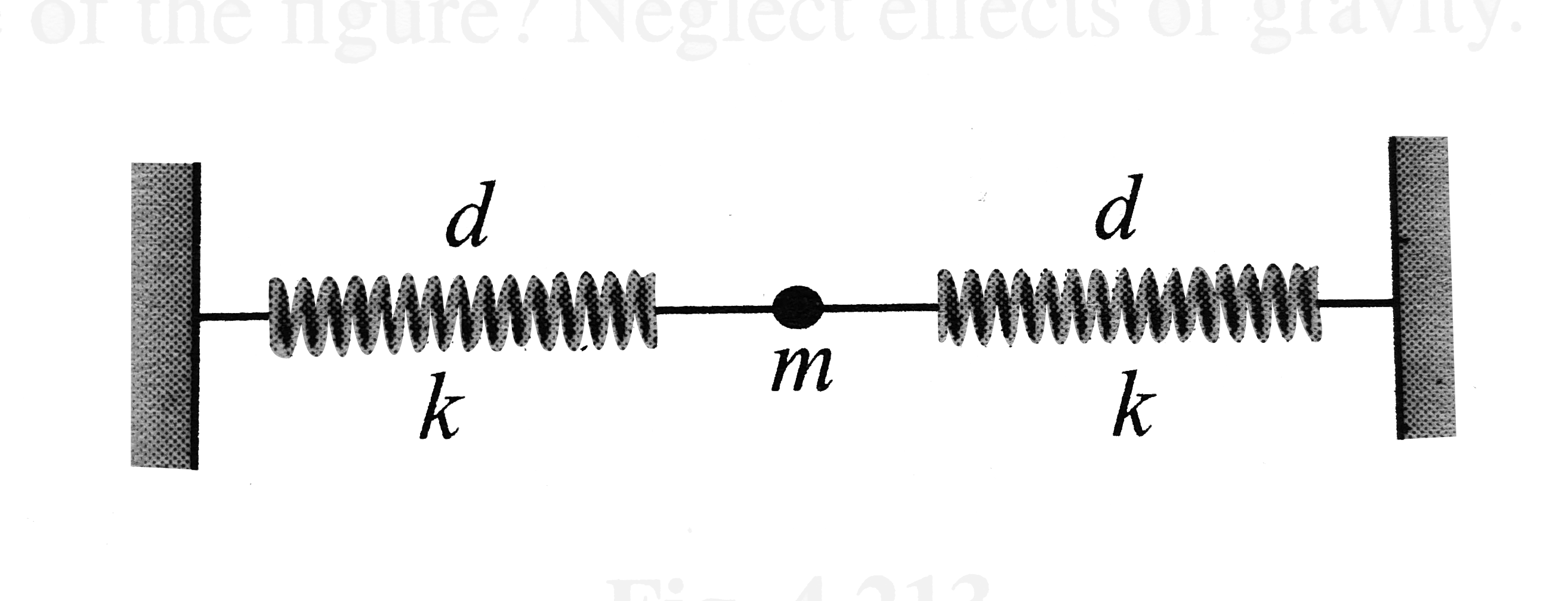
A small body of mass m is connected to two horizontal spring of elastic constant k, natural length 3d4. In the equilibrium position botgh springs are stretched to length d, as shown in Fig. What will be the ratio of perod of the motion (TbTa) If the body is displaced horizontally by a small distance where Ta is the time period when the particle owscillates along the line of spring Tb is time plane of the figure? Neglect effect of gravity.
The correct Answer is:2
Initial stretch in both springs =d−3d4=d4
Fres→r∈g=k(d4+x)−k(d4−x)=2kx=ω21x
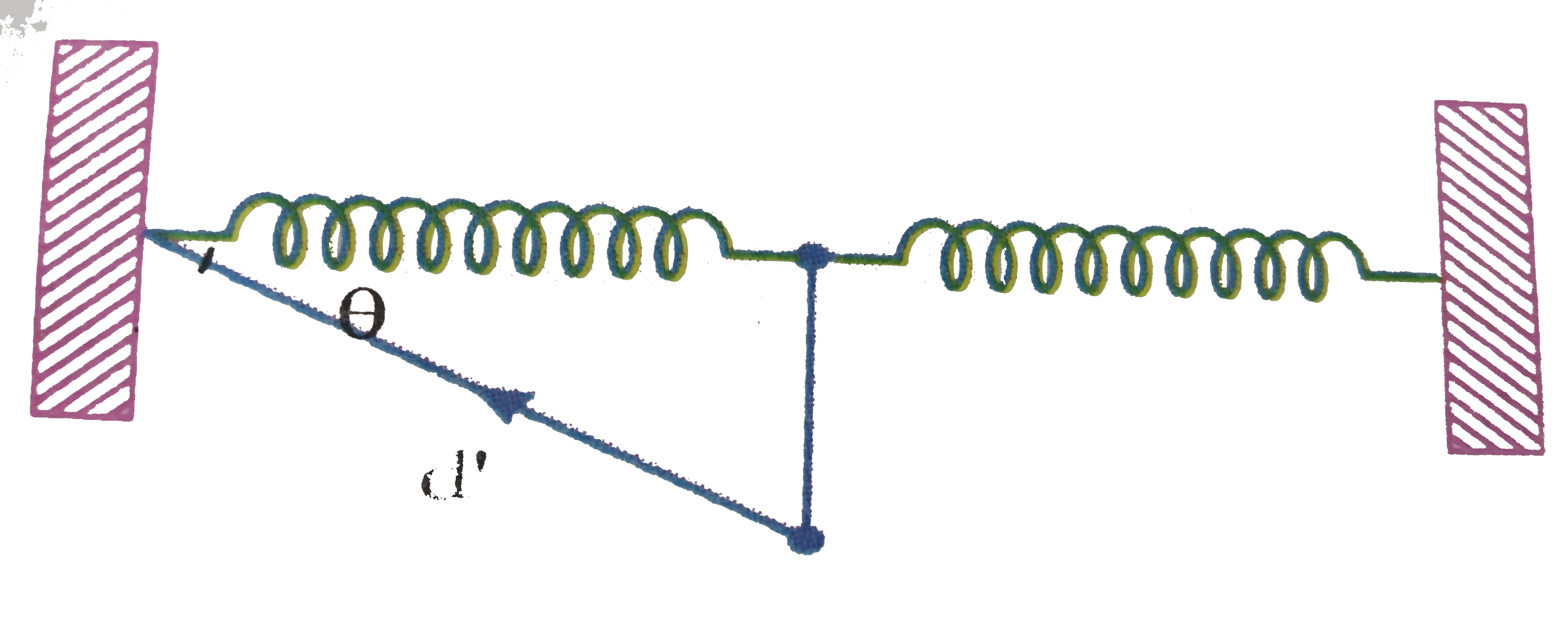
d1=dsecθ,∴X'=dsecθ−3d4
force towads equilibrium position =(kx'sinθ), due to one spring =2(kx'sinθ), due two springs for small θ, force =k(d.θ2)=ω22θ⇒TBTA=2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT6videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII1videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution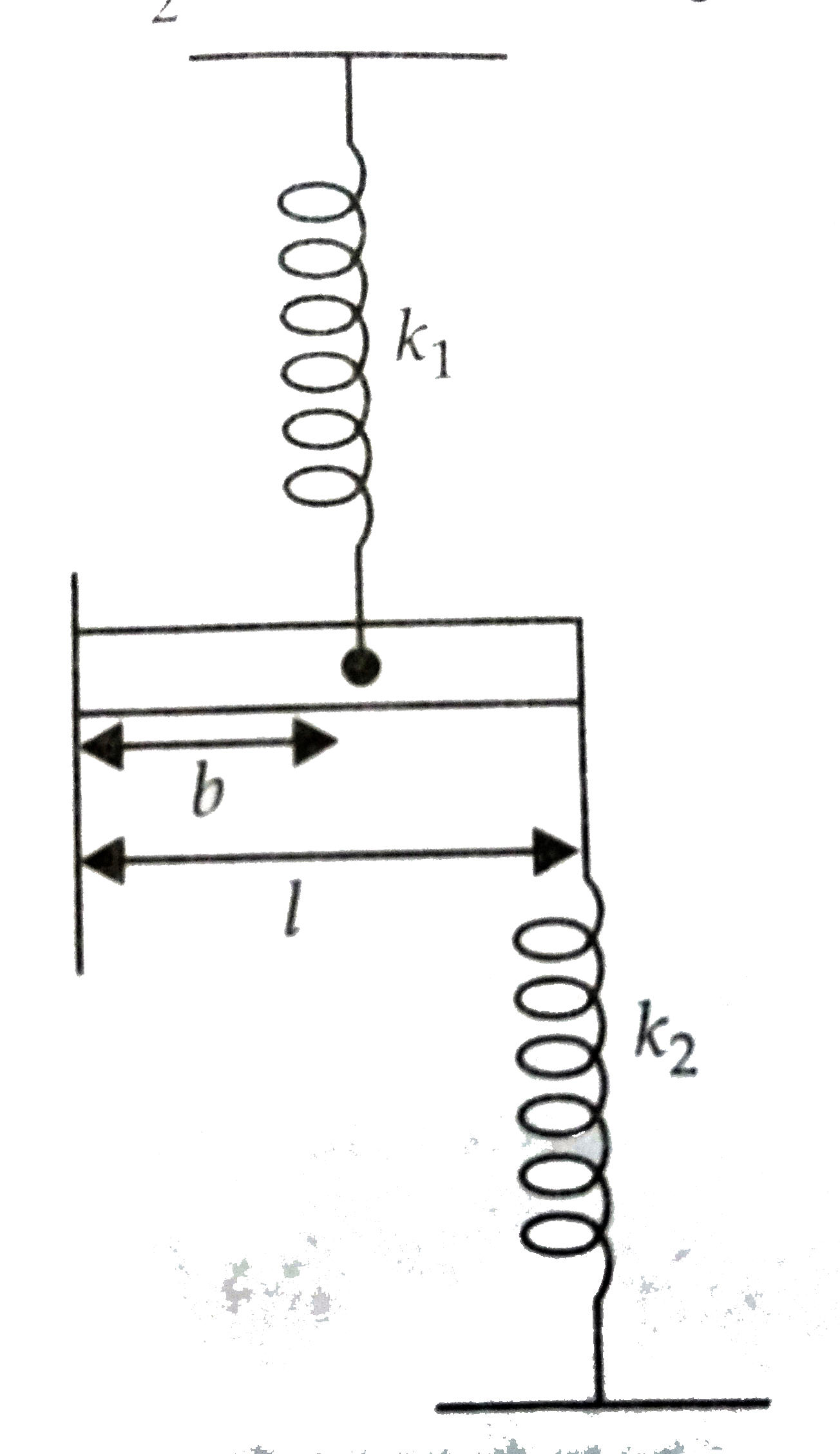
A rod of mass m and length l is connected by two spring of spring constants k1andk2, so that it is horizontal at equilibrium. What is the natural frequency of the system?View Solution
Knowledge Check
- Question 1 - Select One
The frequency of oscillations of a mass m connected horizontally by a spring of spring constant k is 4 HZ. When the spring is replaced by two identical spring as shown in figure. Then the effective frequency is
 A4√2B1.5C1.31D2√2
A4√2B1.5C1.31D2√2 - Question 2 - Select One
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1 - Question 3 - Select One
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
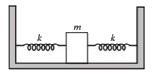 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2k

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.View SolutionThe springs in fig. A and B are identical but length in A is three times each of that in B. The ratio of period TA/TB is
 View Solution
View SolutionA body of mass m is suspended from a massless spring of natural length l. It stretches the spring through a vertical distance y. The potential energy of the stretched spring is
View SolutionA ball of mass mkg hangs from a spring of spring constant k. The ball oscillates with a period of T seconds if the ball is removed, the spring is shortened(w.r.t. length in mean position) by
View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
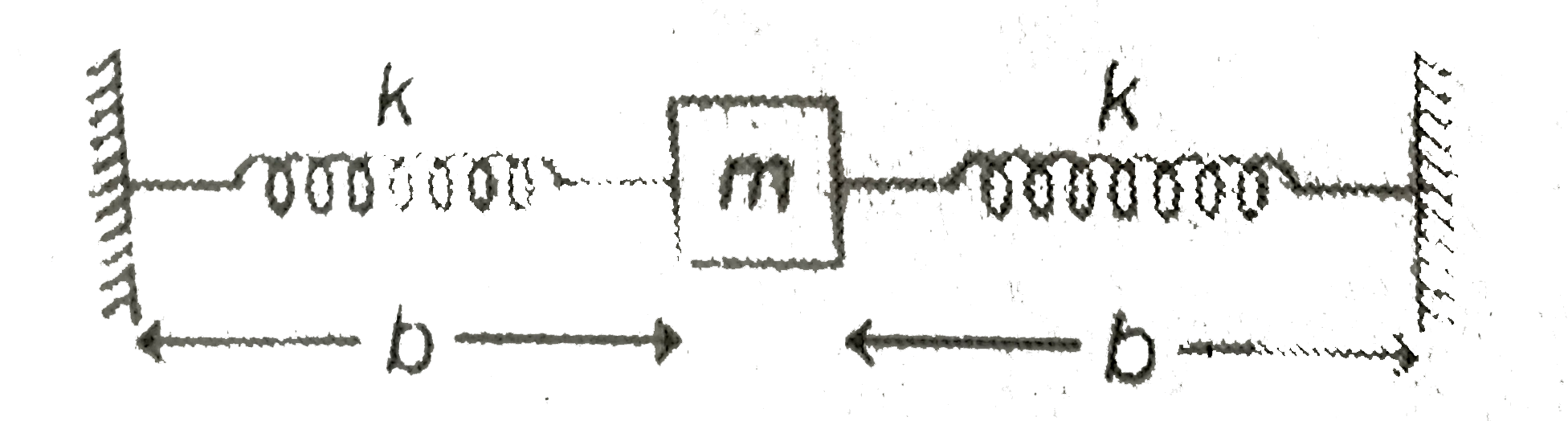 View Solution
View Solution

