Two point masses m and 2m initially at rest are at separation R apart and due to the mutual gravitational force they come togther and collide elastically and then separates and the process continues. The time period of the resulting oscillations is π√Rxg, the value of x is__________(Take g=GmR2)
The correct Answer is:6
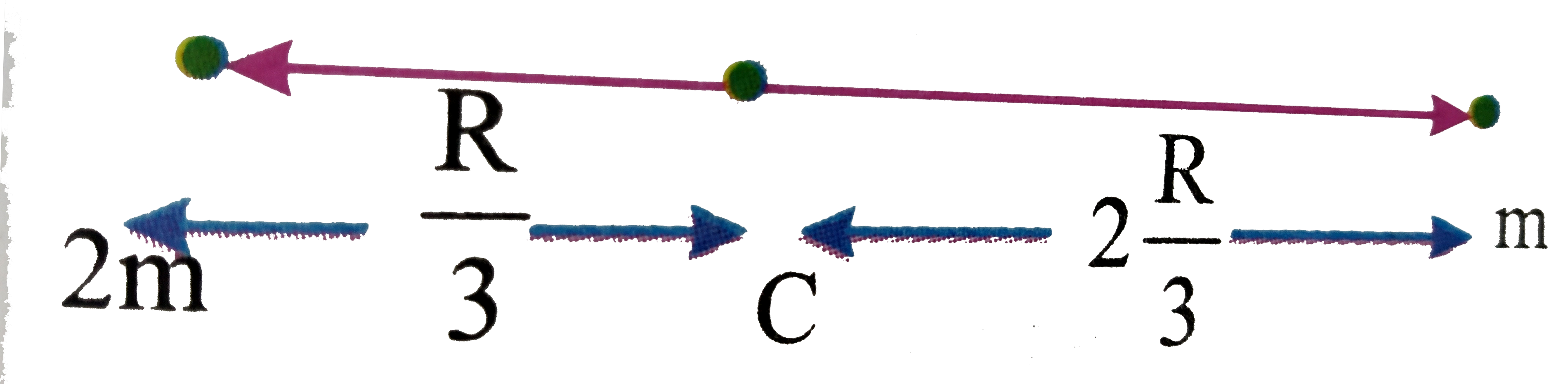
keep a mass M' at the centre of mass for 2m such that
GM'(2m)(R/3)2=G(2m)m(R)2⇒M'=m9
⇒2π(R/3)√GM'(R/3)
⇒T=2π√GM'(R3)3/2
T'=24√2=2π√GM9=R3/2√27
T'=4πR√R4√6√gR2=π√6√Rg
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)
1 Video
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT
6 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII
1 Video
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Two objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
View SolutionTwo spheres of masses 2M and M are initially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of spheres would be
View Solution
Knowledge Check
Two objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
Athe total energy of the two objects is zeroBnet angular momentum of both the objects is zero about any pointCthe total K.E. of the objects is 4Gm2/rDtheir relative velocity of approach is
(8Gmr)1/2Two spheres of masses 2 M and M are intially at rest at a distance R apart. Due to mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the centre of mass of sphere would be
A0m/s2Bgm/s2C3gm/s2D12gm/s2Two lead balls of masses m and 5m having radii R and 2R are separated by 12R. If they attract each other by gravitational force, the distance covered by small sphere before they touch each other is
A10RB7.5RC9RD2.5R
Two particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionTwo particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View SolutionTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionTwo bodies of masses m and 2m are kept at distance r apart from each other. Then the value of G varies as
View Solution
