A body of mass 3kg is moving alone a straight line with a velocity of 24ms−1.When it is at a point P a force of 9N acts on the body in a direction opposite to its motion.The time after which it will be at P again is.
8s
16s
12s
24s
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the body under the influence of the force acting opposite to its direction of motion.
Step 1: Identify the given data
- Mass of the body, m=3kg
- Initial velocity, u=24m/s
- Force acting on the body, F=9N
Step 2: Calculate the acceleration
Using Newton's second law, we can find the acceleration a caused by the force:
F=m⋅a⟹a=Fm
Substituting the values:
a=9N3kg=3m/s2
Since the force is acting in the opposite direction to the motion, the acceleration will be negative:
a=−3m/s2
Step 3: Determine the time to come to a stop
We need to find the time t1 it takes for the body to come to a stop (final velocity v=0):
Using the equation of motion:
v=u+a⋅t
Setting v=0:
0=24m/s−3m/s2⋅t1
Solving for t1:
3m/s2⋅t1=24m/s⟹t1=243=8s
Step 4: Determine the distance traveled before stopping
Now we calculate the distance S1 traveled before the body comes to a stop using the equation:
S=u⋅t+12at2
Substituting the known values:
S1=24⋅8+12⋅(−3)⋅(82)
Calculating each term:
S1=192−12⋅3⋅64=192−96=96m
Step 5: Determine the time to return to point P
After coming to a stop, the body will start moving back towards point P with the same acceleration. The time t2 to return to point P can be found using the same equations of motion. The initial velocity for this motion is 0 and the distance to cover is 96m:
Using the equation:
S=u⋅t+12at2
Setting u=0:
96=0+12⋅3⋅t22
Solving for t2:
96=32t22⟹t22=96⋅23=64⟹t2=8s
Step 6: Calculate the total time
The total time T taken to return to point P is:
T=t1+t2=8s+8s=16s
Final Answer
The time after which the body will be at point P again is 16s.
- Mass of the body, m=3kg
- Initial velocity, u=24m/s
- Force acting on the body, F=9N
Using Newton's second law, we can find the acceleration a caused by the force:
F=m⋅a⟹a=Fm
Substituting the values:
a=9N3kg=3m/s2
Since the force is acting in the opposite direction to the motion, the acceleration will be negative:
a=−3m/s2
We need to find the time t1 it takes for the body to come to a stop (final velocity v=0):
Using the equation of motion:
v=u+a⋅t
Setting v=0:
0=24m/s−3m/s2⋅t1
Solving for t1:
3m/s2⋅t1=24m/s⟹t1=243=8s
Now we calculate the distance S1 traveled before the body comes to a stop using the equation:
S=u⋅t+12at2
Substituting the known values:
S1=24⋅8+12⋅(−3)⋅(82)
Calculating each term:
S1=192−12⋅3⋅64=192−96=96m
After coming to a stop, the body will start moving back towards point P with the same acceleration. The time t2 to return to point P can be found using the same equations of motion. The initial velocity for this motion is 0 and the distance to cover is 96m:
Using the equation:
S=u⋅t+12at2
Setting u=0:
96=0+12⋅3⋅t22
Solving for t2:
96=32t22⟹t22=96⋅23=64⟹t2=8s
The total time T taken to return to point P is:
T=t1+t2=8s+8s=16s
The time after which the body will be at point P again is 16s.
Topper's Solved these Questions
Similar Questions
A body of mass 4kg moving along a straight line under the action of a force.If kinetic energy varies with time as k=8t .The force acting on the body is ?
View SolutionA body of mass 6.25kg is travelling in a horizontal straight line with a velocity of 3m/ sec when a horizontal force P is applied to it at right angle to the initial direction of motion. If P varies according to the accompanying graph, remains constant in direction and is the only force acting on the body in its plane of motion,find the magnitude of the velocity of the body when t=2 sec.
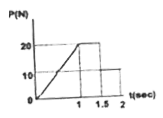 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A body of mass 3 kg is moving along a straight line with a velocity of 24ms−1. When it is at a point ‘P’ a force of 9 N acts on the body in a direction opposite to its motion. The time after which it will be at 'P' again is,
A8sB16sC12sD24s - Question 2 - Select One
A body of mass 1kg is moving along a straight line with a velocity of 1m/s. The external force acting in the body is
A1NB1 dyneC1JDzero - Question 3 - Select One
A body of mass 2kg is moving on a smooth floor in straight line with a uniform velocity of 10m/s Resultant force on the body is
A20NB10NC2NDZero
A body of mass 2 kg is moving in straight line for which v - x graph is shown in the figure. Magnitude of force acting on the body at x = 10 m is 5k N. Find the value of k.
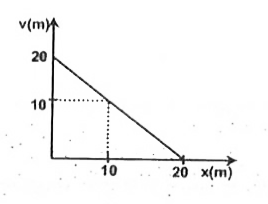 View Solution
View SolutionA body of mass 5kg is moving in a circle of radius 1 m with an angular velocity of 2 rad-s−1. The centripetal force acting on the body is
View SolutionA body of mass 5 kg is moving with a momentum of 10kgms−1. A force of 0.2 N acts on it in the direction of motion of body for 10 s. The increase in its kinetic energy is
View SolutionA body of massm is moving in a straight line with momentum p. Starting at time t = 0, a force F = at acts in the same direction on the moving particle during time interval of T. So that its momentum changes from p to 2p. The value of T is
View SolutionA body of mass 5 kg is moving in a straight line. The relation between its displacement and time t is given by x=(t3−2t−10) metre. What is the force acting onit at the end of second?
View Solution

