A body of massm is moving in a straight line with momentum p. Starting at time t = 0, a force F = at acts in the same direction on the moving particle during time interval of T. So that its momentum changes from p to 2p. The value of T is
√2pa
√pa
√2pa
2pa
The correct Answer is:D
To solve the problem step by step, we will use the relationship between force, momentum, and time.
Step 1: Understand the relationship between force and momentum
The force F acting on the body is given by the rate of change of momentum:
F=dpdt
where p is the momentum of the body.
Step 2: Substitute the given force
According to the problem, the force is given as:
F=at
where a is a constant and t is time.
Step 3: Set up the equation
From the relationship established in Step 1, we can write:
at=dpdt
Step 4: Rearrange the equation
Rearranging gives us:
dp=atdt
Step 5: Integrate both sides
Now, we will integrate both sides. The initial momentum is p at t=0 and changes to 2p at t=T:
∫2ppdp=∫T0atdt
Step 6: Solve the left side
The left side integrates to:
2p−p=p
Step 7: Solve the right side
The right side integrates as follows:
∫T0atdt=a(t22)T0=aT22
Step 8: Set the equations equal
Now we set the results of the integrals equal to each other:
p=aT22
Step 9: Solve for T
Rearranging gives us:
T2=2pa
Taking the square root of both sides, we find:
T=√2pa
Final Answer
Thus, the value of T is:
T=√2pa
The force F acting on the body is given by the rate of change of momentum:
F=dpdt
where p is the momentum of the body.
According to the problem, the force is given as:
F=at
where a is a constant and t is time.
From the relationship established in Step 1, we can write:
at=dpdt
Rearranging gives us:
dp=atdt
Now, we will integrate both sides. The initial momentum is p at t=0 and changes to 2p at t=T:
∫2ppdp=∫T0atdt
The left side integrates to:
2p−p=p
The right side integrates as follows:
∫T0atdt=a(t22)T0=aT22
Now we set the results of the integrals equal to each other:
p=aT22
Rearranging gives us:
T2=2pa
Taking the square root of both sides, we find:
T=√2pa
Thus, the value of T is:
T=√2pa
Topper's Solved these Questions
Similar Questions
A particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View SolutionThe position of a particle moving along the straight line is given as s= (t^(2)-4t+3)m where t is time in s .The magnitude of displacement of the particle during time interval t=0 to till its velocity becomes zero
View Solution
Knowledge Check
Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
Ais constantBis increasingCis decreasingDfirst increase and then decreasesVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
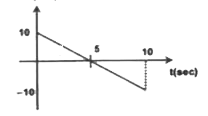 A300JB−300JCzeroD−400J
A300JB−300JCzeroD−400JKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particleBInversely proportional to √tCInversely proportional to the speed of the particleDDirectly proportional to √t
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA body of mass 5 kg is moving in a straight line. The relation between its displacement and time t is given by x=(t3−2t−10) metre. What is the force acting onit at the end of second?
View SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionThe momentum of a particle moving in straight line is given by
p=t+1t(in m/s)
find the (time t>0) at which the net force aciting on particle is 0 and it's momentum at that time.
View SolutionMomentum of a body moving in a straight line is p=(2t3+t2+1) kg m/s. Force (dp/dt) acting on a body at t=2 sec.
View Solution
