Question

Two identical smooth balls are projected towards each other from points $A$ and $B$ on the horizontal ground with same speed of projection. The angle of projection in each case is ${30}^{\circ }$. The distance between $A$ and $B$ is $100m$. The balls collide in air and return to their respective points of projection. If coefficient of restitution is $e=0.7$, find
(a) the speed of projection of either ball.
(b) coordinates of point with respect to a point of projection of $A$, where the balls collide.
(Take $g=10m/s^2$)

Answer

(a) `mu = 37.5 m//s` , (b) `(50 m, 17 m)`

Explanation

(a) By symmetry we can say that they will collide at `x = 50 m`.
Vertical component of velocity and hence time of flight does not change in collision.
Hence

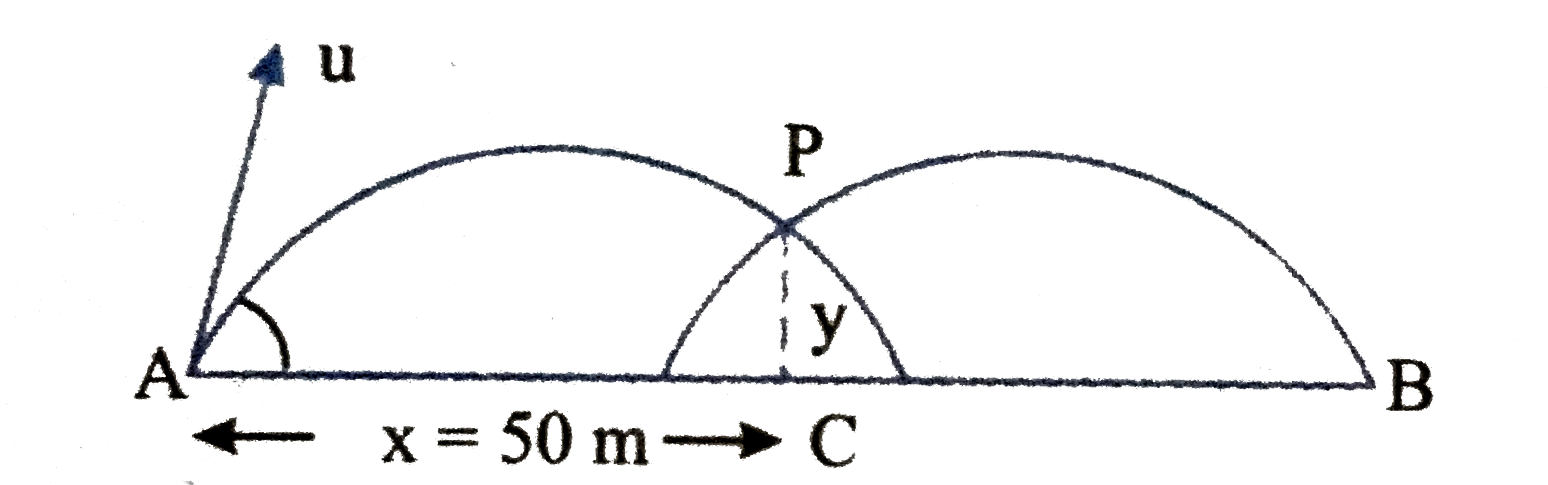
`T_(A) = t_(AC)+t_(CA)`
`(2u sin 30^(circ))/(g) = (50)/(u cos 30^(circ))+(50)/(e u cos 30^(circ))`
Given `g = 10 m//s^(2), e = 0.7`.
Substituting the values we get `u = 37.5 m//s`
(b) ` y = x tan 30^(circ)-(g x^(2))/(2 u^(2) cos ^(2) 30^(circ))`
`x = 50m, u = 37.5 m//s`
Substituting the values we get `y = 17 m`
Hence, coordinates of point `P` w.r.t. `A` are `(50 m, 17 m)`.