A rectangular block has dimensions 5cm×5cm×10cm. Calculate the resistance measured between (a) two square ends and (b) the opposite rectangular ends. Specific resistance of the material is 3.5×10−5Ωm.
To solve the problem of calculating the resistance of a rectangular block with given dimensions and specific resistance, we will follow these steps:
Given Data:
- Dimensions of the block: 5cm×5cm×10cm
- Specific resistance (ρ): 3.5×10−5Ω⋅m
Step 1: Convert Dimensions to Meters
Convert the dimensions from centimeters to meters:
- 5cm=0.05m
- 10cm=0.10m
Step 2: Calculate Resistance Between Two Square Ends
(a) The area of the square ends:
- Area A=side2=(0.05m)2=0.0025m2
(b) The length L between the square ends:
- Length L=0.10m
(c) Use the formula for resistance:
R=ρLA
Substituting the values:
R=3.5×10−5Ω⋅m×0.10m0.0025m2
Calculating:
R=3.5×10−60.0025=1.4×10−3Ω
Step 3: Calculate Resistance Between Opposite Rectangular Ends
(a) The area of the rectangular ends:
- Area A=length×width=0.10m×0.05m=0.005m2
(b) The length L between the rectangular ends:
- Length L=0.05m
(c) Use the formula for resistance:
R=ρLA
Substituting the values:
R=3.5×10−5Ω⋅m×0.05m0.005m2
Calculating:
R=1.75×10−60.005=0.35×10−3Ω=3.5×10−4Ω
Final Answers:
- (a) Resistance between two square ends: 1.4×10−3Ω
- (b) Resistance between opposite rectangular ends: 3.5×10−4Ω
- Dimensions of the block: 5cm×5cm×10cm
- Specific resistance (ρ): 3.5×10−5Ω⋅m
Convert the dimensions from centimeters to meters:
- 5cm=0.05m
- 10cm=0.10m
(a) The area of the square ends:
- Area A=side2=(0.05m)2=0.0025m2
- Length L=0.10m
R=ρLA
Substituting the values:
R=3.5×10−5Ω⋅m×0.10m0.0025m2
Calculating:
R=3.5×10−60.0025=1.4×10−3Ω
(a) The area of the rectangular ends:
- Area A=length×width=0.10m×0.05m=0.005m2
- Length L=0.05m
R=ρLA
Substituting the values:
R=3.5×10−5Ω⋅m×0.05m0.005m2
Calculating:
R=1.75×10−60.005=0.35×10−3Ω=3.5×10−4Ω
- (a) Resistance between two square ends: 1.4×10−3Ω
- (b) Resistance between opposite rectangular ends: 3.5×10−4Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - C.U.Q
105 Videos
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 C.W
64 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
A rectabgykar carbon block has dimensions 1.0cm×1.0×50cm.
(i) What is the resistance measured between the two square ends ?
(ii) Between two opposing rectangular faces ?
Resistivity of carbon at 20∘C is 3.5×10−5Ωm.
View SolutionA rectangular carbon block has dimensions 1.0 cm×1.0 cm×50 cm. Resistance are measured , first across two square ends and then across two respectivelt . If resistivity of carbon is 3.5×10−5Ω-m , then values of measured resistance respectively are :
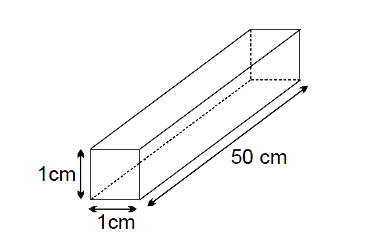
View Solution
Knowledge Check
The size of a carbon block, having specific resistance. 3.5×10−3Ω−cm is 2cm×2cm×2cm. The resistance of the block between two square end faces and two opposite rectangular faces are respectively
A17.5×10−4 and 1.75×10−4ΩB1.75×10−4 and 175×10−4ΩC175×10−4 and 1.75×10−4ΩD1.75×10−4 and 17.5×10−4ΩThe dimensions of a block are 1cm×1cm×100cm. If the specific resistance of its material is 2×10−7ohm×metre, then the resistance between the opposite rectangular faces is
A2×10−9ΩB2×10−7ΩC2×10−5ΩD2×10−3ΩDimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm-m, then the resistance between the opposite rectangular faces is
A3×10−9 ohmB3×10−7 ohmC3×10−5 ohmD3×10−3 ohm
A wooden block of dimensions 10cm×20cm×50cm weighs 6-5 kg Calculate the density of the block.
View SolutionThe size of a carbon block is 1.0×10cm×50cm. Find its resistance (i) between the opposite square faces (ii) between the opposite rectangular faces of the block. The resistivity of carbon is 3.5×10−5Ωcm.
View SolutionCalculate the resistance of a hollow cylinder made of copper with inner radius 3 cm and outer radius 3.5 cm and is 12 cm long. (Speciffic resistance of copper is 1.68×10−8Ωm)
View SolutionA wire of resistance 5.0Ω is used to wind a coil of radius 5 cm. The wire has a diameter 2.0 mm and the specific resistance of its material is 2.0×10−7Ωm. Find the number of turns in the coil.
View SolutionDimensions of a block are 1cm×1cm×10cm. If specific resistance of its material is 3×10−7ohm-m, then the resistance between the opposite rectangular faces is
View Solution
