Two conducting layers of length L each specific resistivites ρ1 and ρ2 and cross-sectional areas A1 and A2 respectively are connected to a voltage source V such that current flow lines do not cross from one layer to the other.
(i). Find the total current in the system and describe how it is divided between the 2 layers
(ii). Find the total current when a third layer of cross-sectional area A1+A2, length L and specific resistivity ρ3 is attached at one of the ends of the given system.
The correct Answer is:(i). (vR1R2(R1+R2))×R1
(vR1R2(R1+r2))R2
(ii). vR1R2R1+R2+R3 where R1=ρ1lA1
(i) resistance of the 2 layers are:
R1=LA1ρ1,R2=LA2ρ2
Hence, total resistance across the voltage source is: 
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NARAYNAChapter:CURRENT ELECTRICITYExercise:Level 5
Explore 42 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:NARAYNAChapter:DUAL NATURE OF RADIATION AND MATTERExercise:ASSERTION AND REASON
Explore 15 Videos
Similar Questions
Two rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View Solution
Knowledge Check
Two wires of equal diameters, of resistivities ρ1 and ρ2 and length l1 and l2, respectively of the combination is
Aρ1l1+ρ2l2l1+l2Bρ1l2+ρ2l1l1−l2Cρ1l2+ρ2l1l1+l2Dρ1l1+ρ2l2l1−l2Two wires of different materials of resistivity p1andp2 , length l1andl2, and area of cross-section A1andA2 respectively are connected in parallel. The ratio of current density in the two wires,j1j2 , is given by:
A(A1A2)(p2p1)(j1j2)B(p2p1)(j2j1)C(A2A1)(p2p1)(j2j1)D(p2p1)(j1j2)The specific resistance and area of cross section of the potentiometer wire are ρ' and A respectively. If a current i passes through the wire, its potential gradient will be
AiρABiρACiAρDiAρ
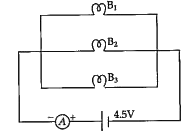
Total current flowing from the battery is 1A. Find the total resistance of the circuit:
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View SolutionTwo cylindrical conductors with equal cross-sections and different resistivites ρ1 and ρ2 are point end to end. Find the charge at the boundary of the conduction if a current I flows from conductor 1 to conductor 2
View SolutionA conductor of length l, area of cross section A and resistivity ρ has resistance = R. It is connected across a cell of voltage V . What will be the current flowing resistor if its length is doubled and cross section area is halved.
View SolutionA current i passes through a wire of length l , radius of cross-section r and resistivity ρ . The rate of heat generation is
View Solution
