
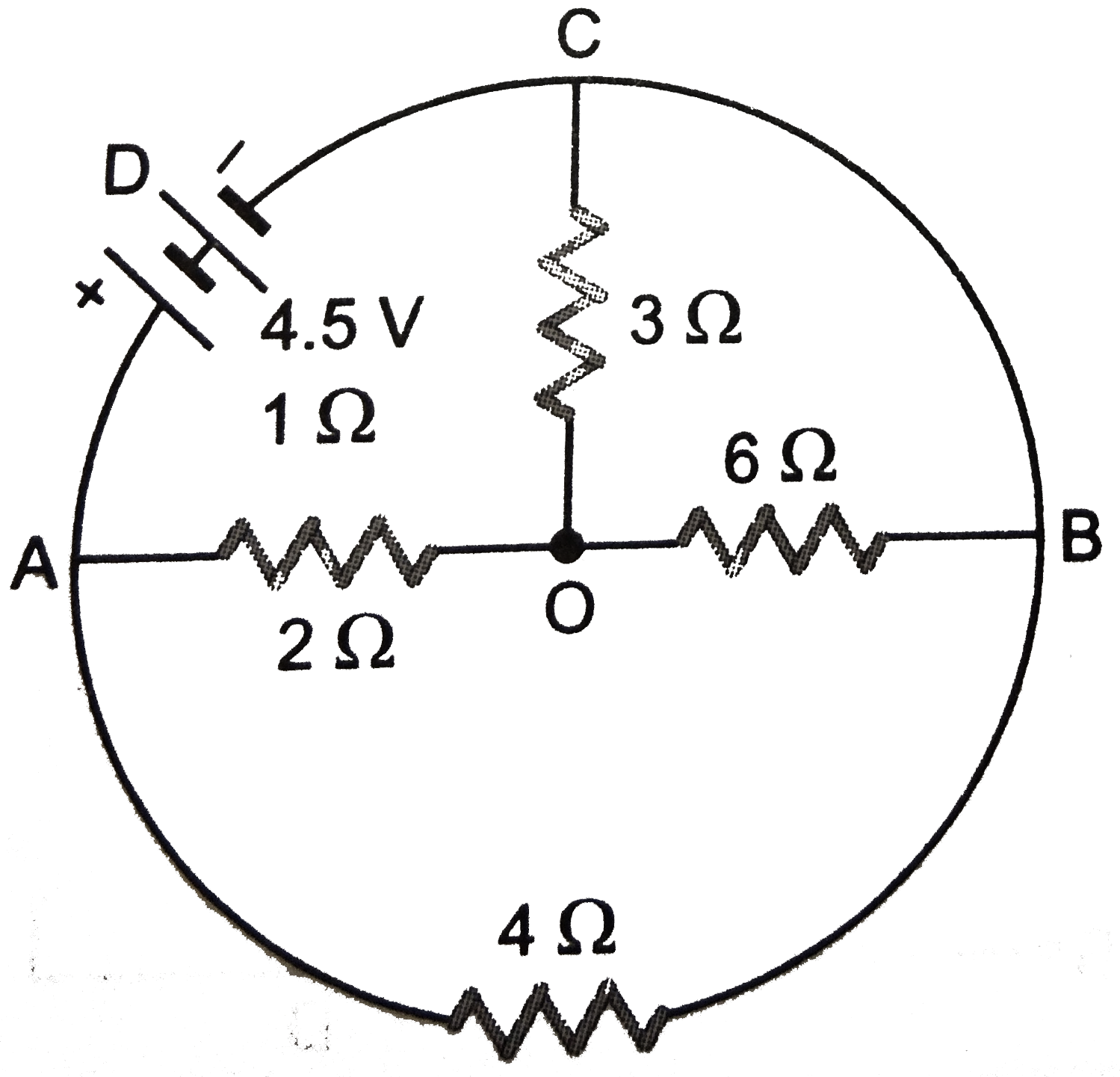
A battery if internal resistance 4Ω is conneted to the network of resistances as shown. What must be the value of R so that maximum power is delivered to the network Find the maximum power?
According to maximum power transfer theorem
Rext=R∫=3R×6R9R=4⇒R=42=2Ω
(ii). Pmax=i2Rext=(E4+4)2×4=E216
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - C.U.Q105videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 C.W64videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
- BOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
(a) A cell of emf E and internal resistance r is connected to a resistance R.
(i) Relate r and R, so that power in R is maximum.
(ii) Maximum power consumed by R.
(iii) Efficiency.
(b) Find value r in terms of R so that power in external circuit is maximum.
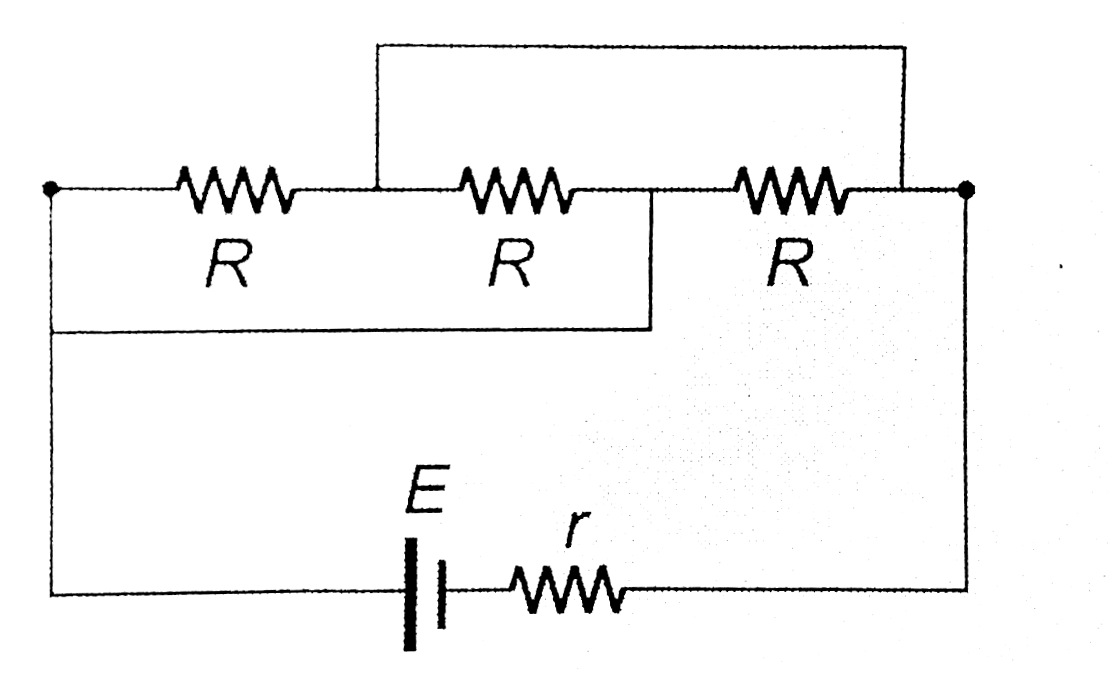
(c) A battery of internal resistance 4Ω is connected to the network of resistance as shown in the figure. what must be the value of R so that maximum power is delivered to the network? what is tha maximum power?
 View Solution
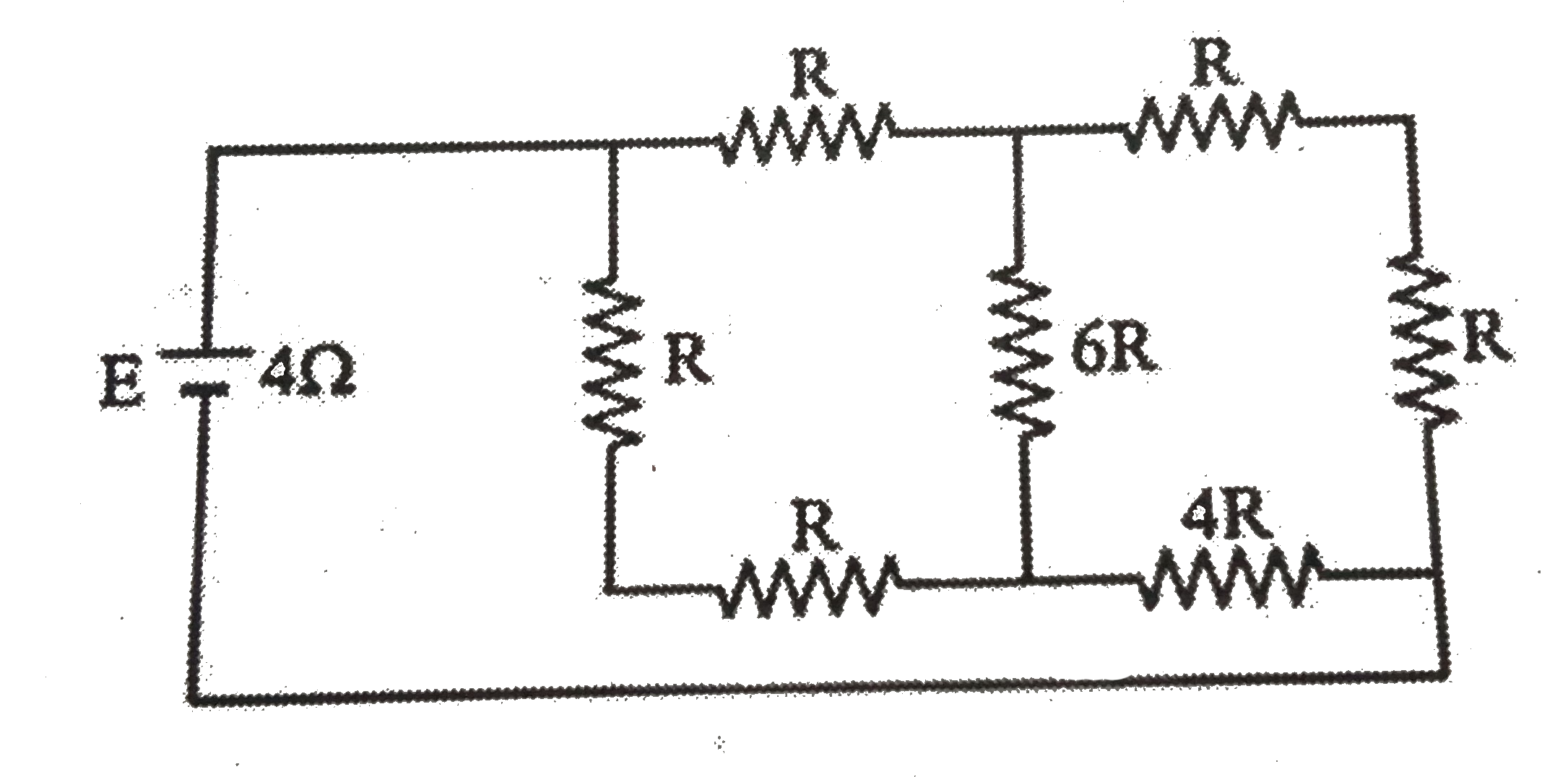
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown. In order to give the maximum power to the network, the value of R should be-
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . A49B2C83D18
. A49B2C83D18 - Question 2 - Select One
A battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . A49B2C83D18
. A49B2C83D18 - Question 3 - Select One
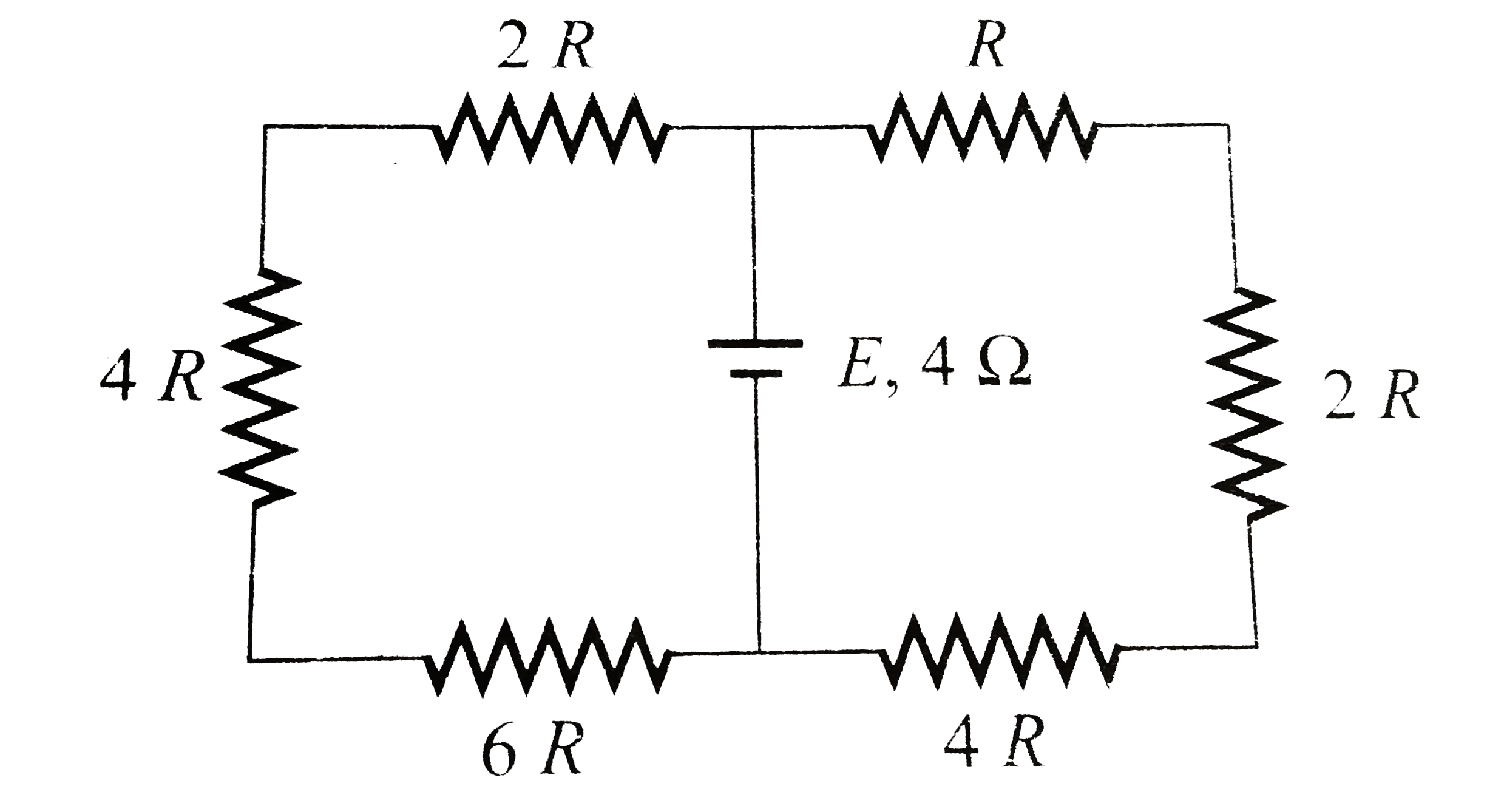
A battery of internal resistance 4Ω is connected to the network of the resistance as shown in figure . If the maximum power can be delivered to the network, the magnitude of resistance in Ωshould be
 A19/21ΩB84/19ΩC12ΩD7Ω
A19/21ΩB84/19ΩC12ΩD7Ω
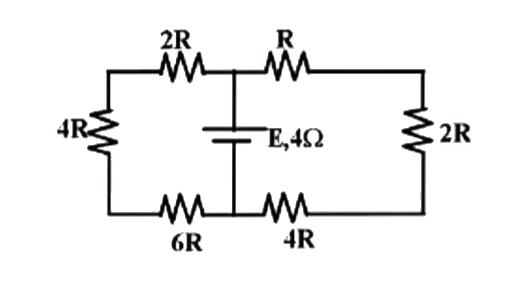
A battery of internal resistance 4Ω is connected to the network of the resistance as shown in figure. To deliver maximum power to the network, the magnitude of resistance R in Ω should be x21. Find x .
 View Solution
View SolutionFind the power dissipated in 3Ω resistance of the network of resistors.
 View Solution
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown. In order to give the maximum power to the network, the value of R should be-
 View Solution
View SolutionA battery is of emt E and internal resistance r. The value of external resistance R so that the power across eternal resistance is maximum :
View Solution

