Two cylindrical conductors with equal cross-sections and different resistivites ρ1 and ρ2 are point end to end. Find the charge at the boundary of the conduction if a current I flows from conductor 1 to conductor 2
The electric field in conductor 1 is
E1=ρ1IπR2
and that in 2 is E2=ρ2IπR2
Appling Gauss's theorem to a small cylindical pill-box at the boundary.
−ρ1IπR2dS+ρ2IπR2dS=σdSε0
Thus, σ=ε0(ρ2−ρ1)1πR2
and charge at the boundary =ε0(ρ2−ρ1)I
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electromagnetic Induction
Explore 84 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Two long straight cylindrical conductors with resistivities ρ1andρ2 repectively are joined together as shown in figure . The radius of each of the conductor is a . If a uniform total current I flows through the conductors , the magnitude of the total free charge at the interface of the two conductor is
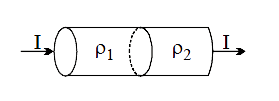
View Solution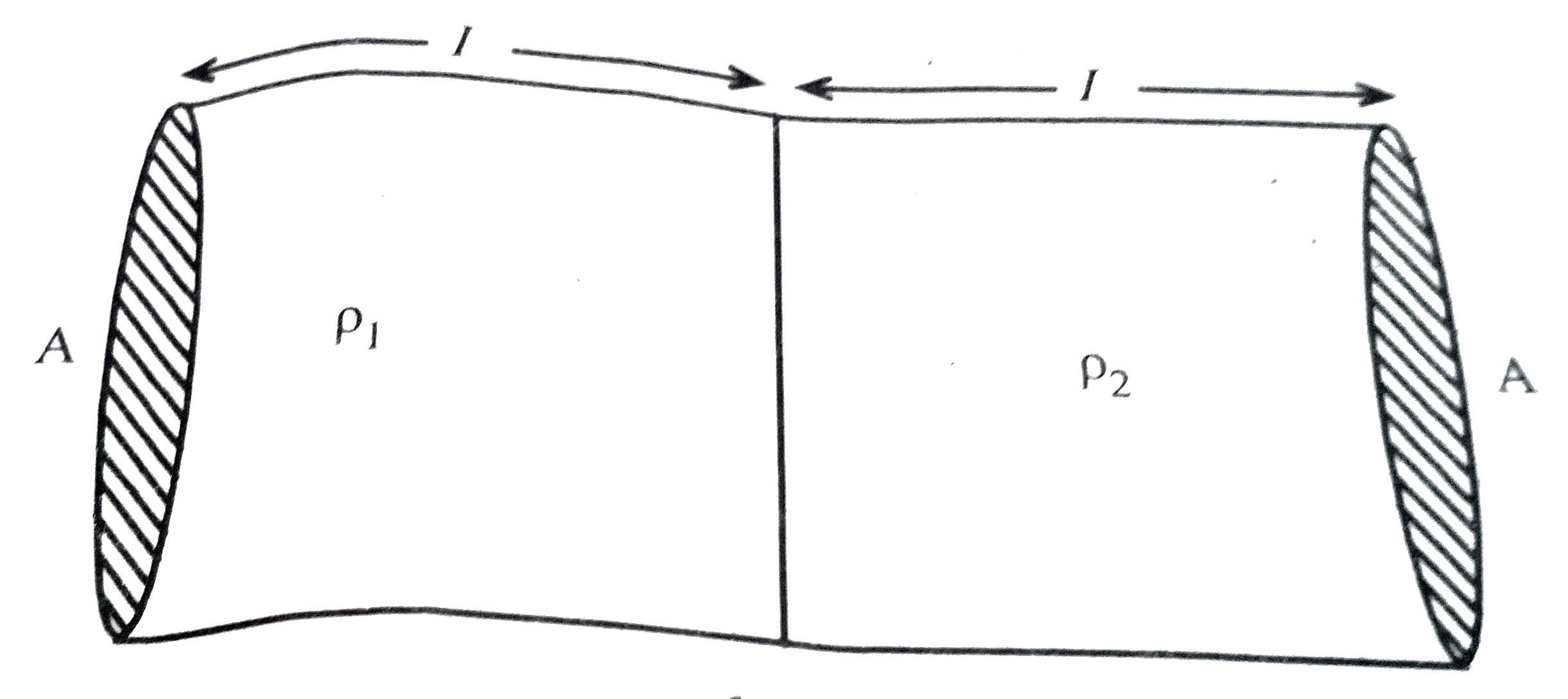
Two rods having equal lengths and equal cross-sections but different specific resistances ρ1 and ρ2 are joined at one end as shown in the figure given above. What is the effective specific resistance of the combination ?
View Solution
Knowledge Check
Consider a conductor of variable cross section in which current is flowing from cross section 1 to 2. Then
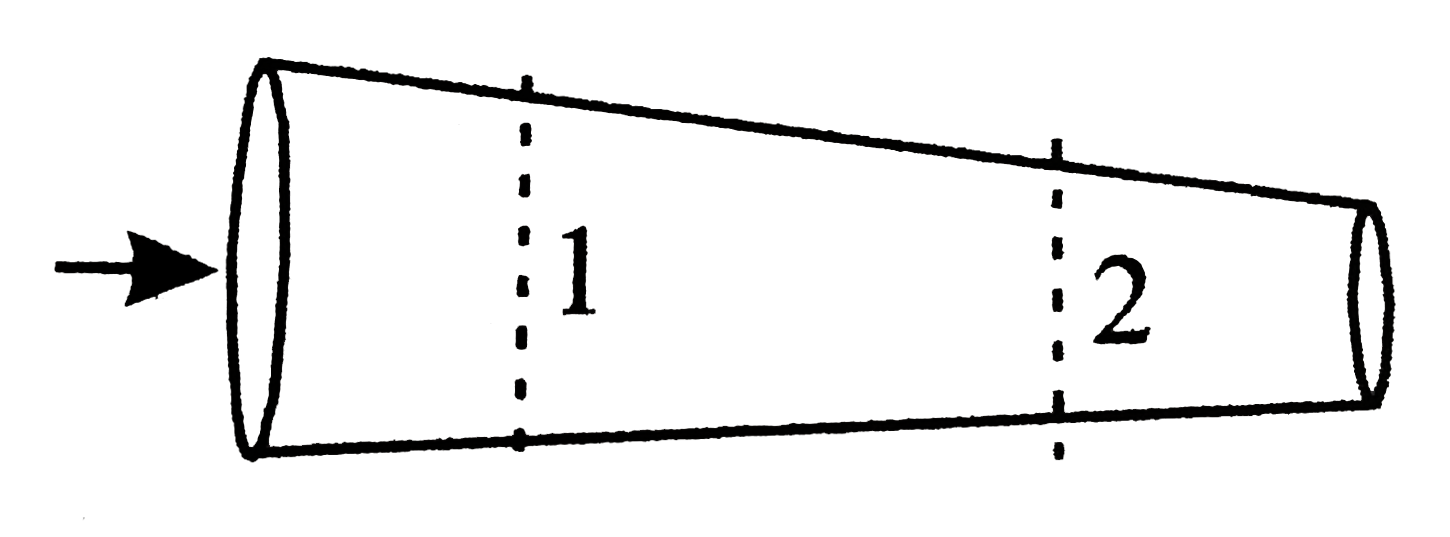 Acurrent passing through both the cross sections in the sameBcurrent through 1 is less then that through 2Cdrift velocity of electrons at 1 is less then that at 2Ddrift velocity is same at both the cross sections
Acurrent passing through both the cross sections in the sameBcurrent through 1 is less then that through 2Cdrift velocity of electrons at 1 is less then that at 2Ddrift velocity is same at both the cross sectionsCharge flows between two ends of a conductor when
Aequal and same type of charges are present at the two endsBdifferent electric potentials exist at the two ends of a conductorCthe potential difference between the ends is zeroDsame electric potential is present at the two endsIf the potential difference across the ends of a conductor is doubled, the current flowing through it gets
AdoubledBhalvedCfour timesDno change
Two cylindrical rods, of different material, are joined as shown. The rods have same cross section (A) and their electrical resistivities are ρ1andρ2. When a current I is passed through the rods, a charge (Q) gets piled up at the junction boundary. Assuming the current density to be uniform throughout the cross section, calculate Q.
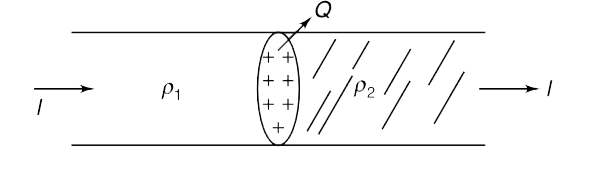
View SolutionTwo conducting layers of length L each specific resistivites ρ1 and ρ2 and cross-sectional areas A1 and A2 respectively are connected to a voltage source V such that current flow lines do not cross from one layer to the other.
(i). Find the total current in the system and describe how it is divided between the 2 layers
(ii). Find the total current when a third layer of cross-sectional area A1+A2, length L and specific resistivity ρ3 is attached at one of the ends of the given system.
View Solution
A cylindrical conductor of length l and inner radius R1 and outer radius R2 has specific resistance ρ. A cell of emf ε is connected across the two lateral faces of the conductor. Find the current drown from the cell.
View SolutionA cylindrical conductor of length l and uniform area of cross-section A has resistance R. Another conductor of length 2l and resistance R of the same material has area of cross-section :
View Solution_2019_CBT4_E01_064_Q01.png)
Two conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is θ1 and that of second conductor is θ2 .the temperature of junction is steady state is (θ2>θ1)
View Solution