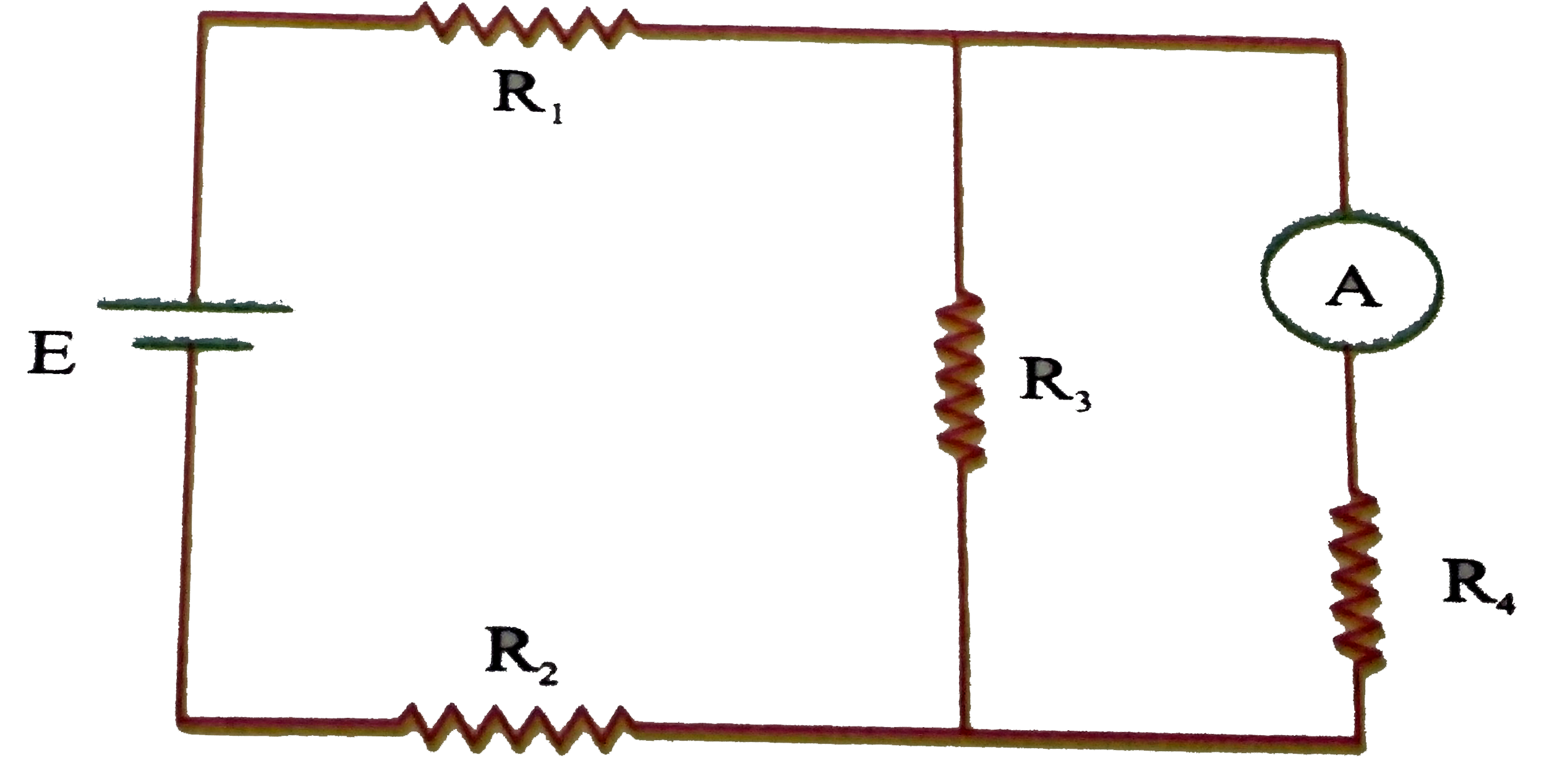
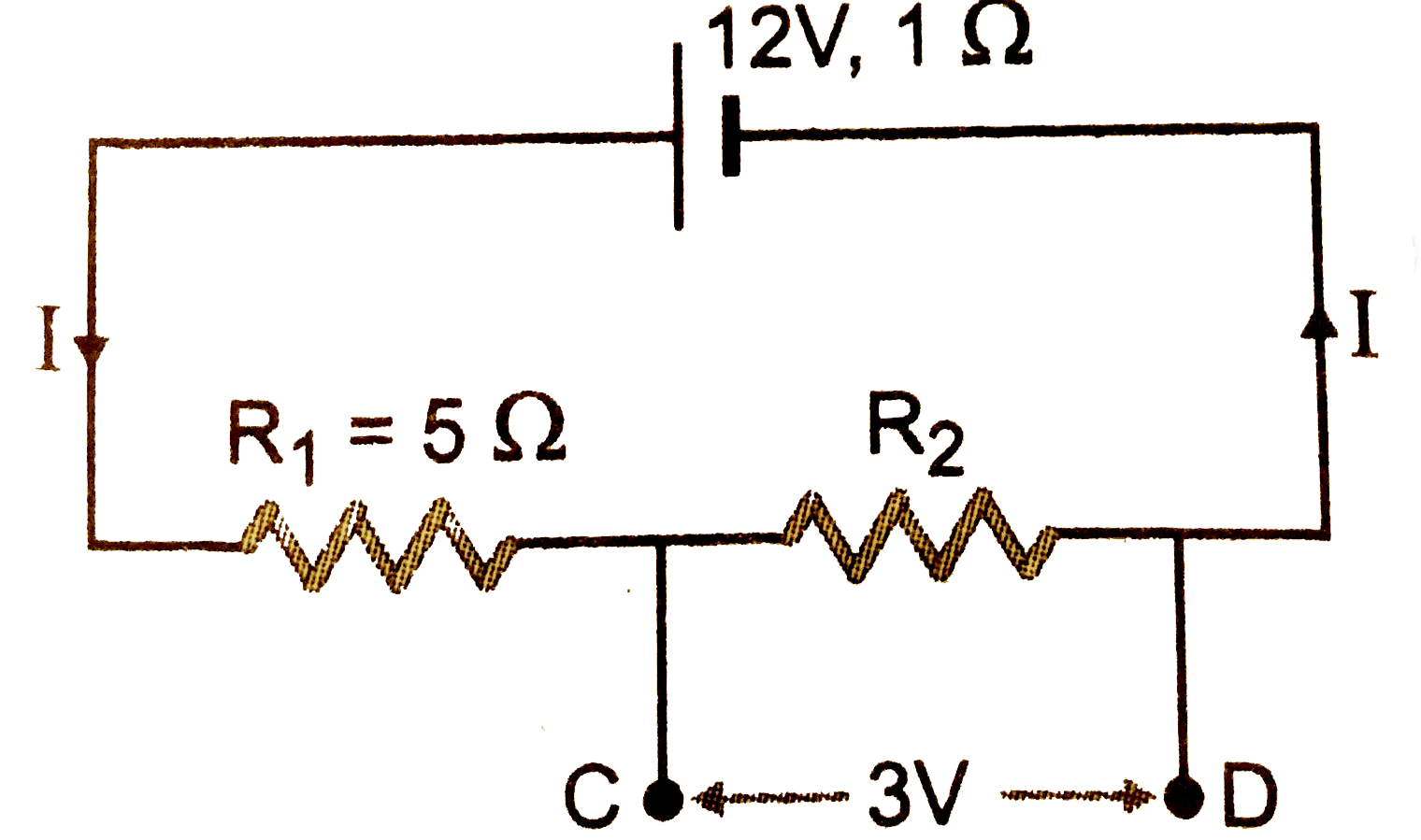Four resistors $R_{1}, R_{2}, R_{3}$ and $R_{4}$ are connected between two terminals A and B iin a network as shown in the diagram. A key K can connect the two points (see diagram) C and D. A constant potential difference $(V_{A} - V_{B}) = V$ is maintained between thhe points A and B
Q. If $R_{1} = R_{4} = 1 Ω$ and $R_{2} = R_{3} = 2 Ω$ , the effective resistance between the terminals A and B will change, on closing the key K, by

A

an increase of $0.5 Ω$

B

a decrease of $0.16 Ω$

C

an increase of $0.16 Ω$

D

a decrease of $0.5 Ω$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let the resistance (small but zero) in the arm CD be x $Ω$ . Assume currents $i_{1}, i_{2}, i_{3}, i_{4}$ and $i_{x}$ as shown in the diagram. Then applications of kirchhoff's junctions and loop laws give,
$i_{1} = i_{2} + i_{x}$ ..(i)
$i_{3} = i_{4} - i_{x}$ ..(ii)
$V = i_{1} R_{1} + i_{1} R_{2} + i_{4} R_{4}$ ..(iii)
and $i_{1} R_{1} + X i_{x} - i_{3} R_{3} = 0$ ..(iv)
Solving these equation for $i_{x}$ we get from (1) & (3)
$V - i_{1} (R_{1} + R_{2}) - i_{x} R_{2}$ ..(v)
and from (2) and (3)
$V - i_{3} (R_{3} + R_{4}) + i_{x} R_{4}$ ...(vi)
Sustituting for $i_{1}$ from (5) and $i_{3}$ from (vi) and (iv)
$R_{1} [\frac{V + i_{x} R_{2}}{R_{1} + R_{2}}] + X i_{2} - R_{3} [\frac{V - i_{x} R_{4}}{R_{3} + R_{4}}] = 0$
Collecting thew terms in
$i_{x}, i_{x} [x + \frac{R_{1} R_{2}}{R_{1} + R_{2}} + \frac{R_{3} R_{4}}{R_{3} + R_{4}}]$
$= V [\frac{R_{3}}{R_{3} + R_{4}} - \frac{R_{1}}{R_{1} R_{2}}]$
$\Rightarrow I_{x} = \frac{V [\frac{R_{3}}{R_{3} + R_{4}} - \frac{R_{1}}{R_{1} + R_{2}}]}{x + \frac{R_{1} R_{2}}{R_{1} + R_{2}} + \frac{R_{3} R_{4}}{R_{3} + R_{4}}}$
Proceeding to limit $x \to 0$ ( $x =$ m negligibly small)
$i_{x} = \frac{25 [\frac{R_{3}}{R_{3} + r_{4}} - \frac{R_{1}}{R_{1} + R_{2}}]}{[\frac{R_{1} R_{2}}{R_{1} + R_{2}} + \frac{R_{3} R_{4}}{R_{3} + R_{4}}]}$ substituting values,
$i_{x} = \frac{25 [\frac{3}{7} - \frac{1}{3}]}{[\frac{2}{3} + \frac{12}{7}]} = \frac{25 \times 2}{50} =$ lamp

Updated on:21/07/2023

|

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Four resistors $R_{1}, R_{2}, R_{3}$ and $R_{4}$ are connected between two terminals A and B iin a network as shown in the diagram. A key K can connect the two points (see diagram) C and D. A constant potential difference $(V_{A} - V_{B}) = V$ is maintained between thhe points A and B
Q. If $V = 25, R_{1} = 1 Ω, R_{2} = 2 Ω, R_{3} = 3 Ω$ and $R_{4} = 4 Ω$ the current that will flow from C to D on connecting key K is
Azero
Binfinity
C $+ 1 A$
D $- 1 A$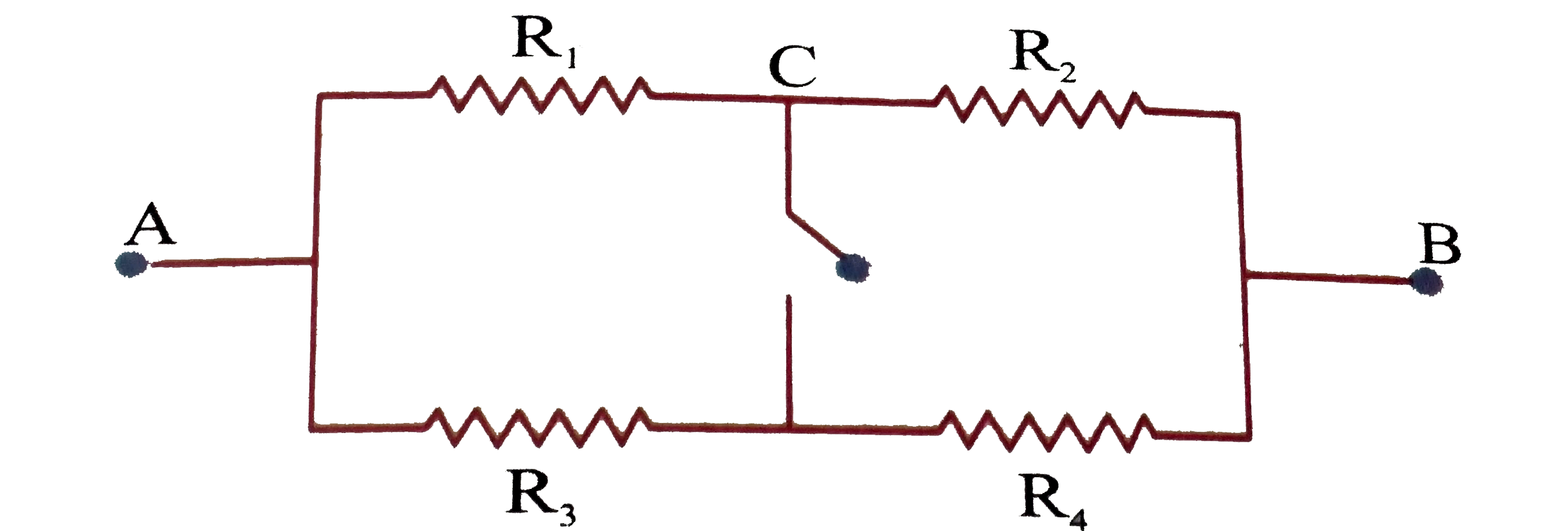
Four resistors $R_{1}, R_{2}, R_{3}$ and $R_{4}$ are connected between two terminals A and B iin a network as shown in the diagram. A key K can connect the two points (see diagram) C and D. A constant potential difference $(V_{A} - V_{B}) = V$ is maintained between thhe points A and B
Q. In on connecting the key K, no current flows through the segment CD, whatever potential difference V exists between A and B which of the following cases will satisfy this condition?
A $R_{1} = 1 Ω, R_{2} = 2 Ω, R_{3} = 3 Ω, R_{4} = 4 Ω$
B $R_{1} = 2 Ω, R_{2} = 1 Ω, R_{3} = 4 Ω, R_{4} = 2 Ω$
C $R_{1} = 1 Ω, R_{2} = 2 Ω, R_{3} = 2 Ω, R_{4} = 1 Ω$
D $R_{1} = R_{2} = 2 Ω, R_{3} = 2 R_{4} = 4 Ω$
An infinite ladder network is arranged with resistances R and 2 R as shown. The effective resistance between terminals A and B is

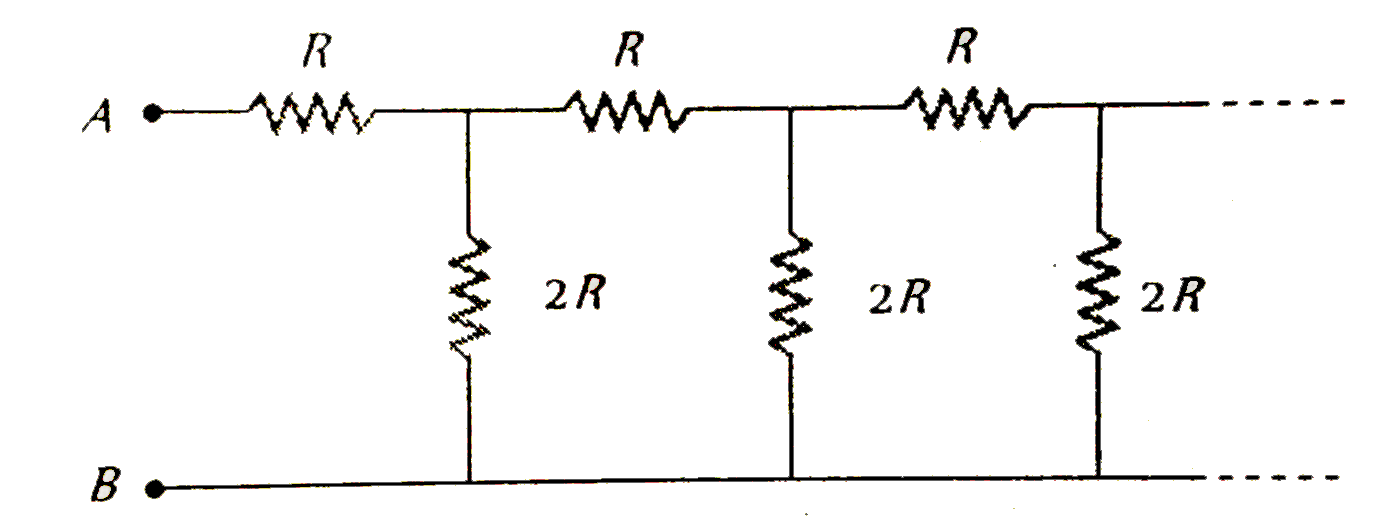A $\infty$
BR
C2R
D3R

NARAYNA-CURRENT ELECTRICITY-Level 6

Home
Ask Doubt
Profile