Twelve straight uniform wires of length a and resistance R are joined to form the edges of a cube of side a. Current enters the system at one corner andd leaves from a point on one of the edges meeting at the opposite corner at a distance Ka(<K<1) from it.
Q. The equivalent resistance is maximum, when
K=45
K=25
K=15
K=0
The correct Answer is:B
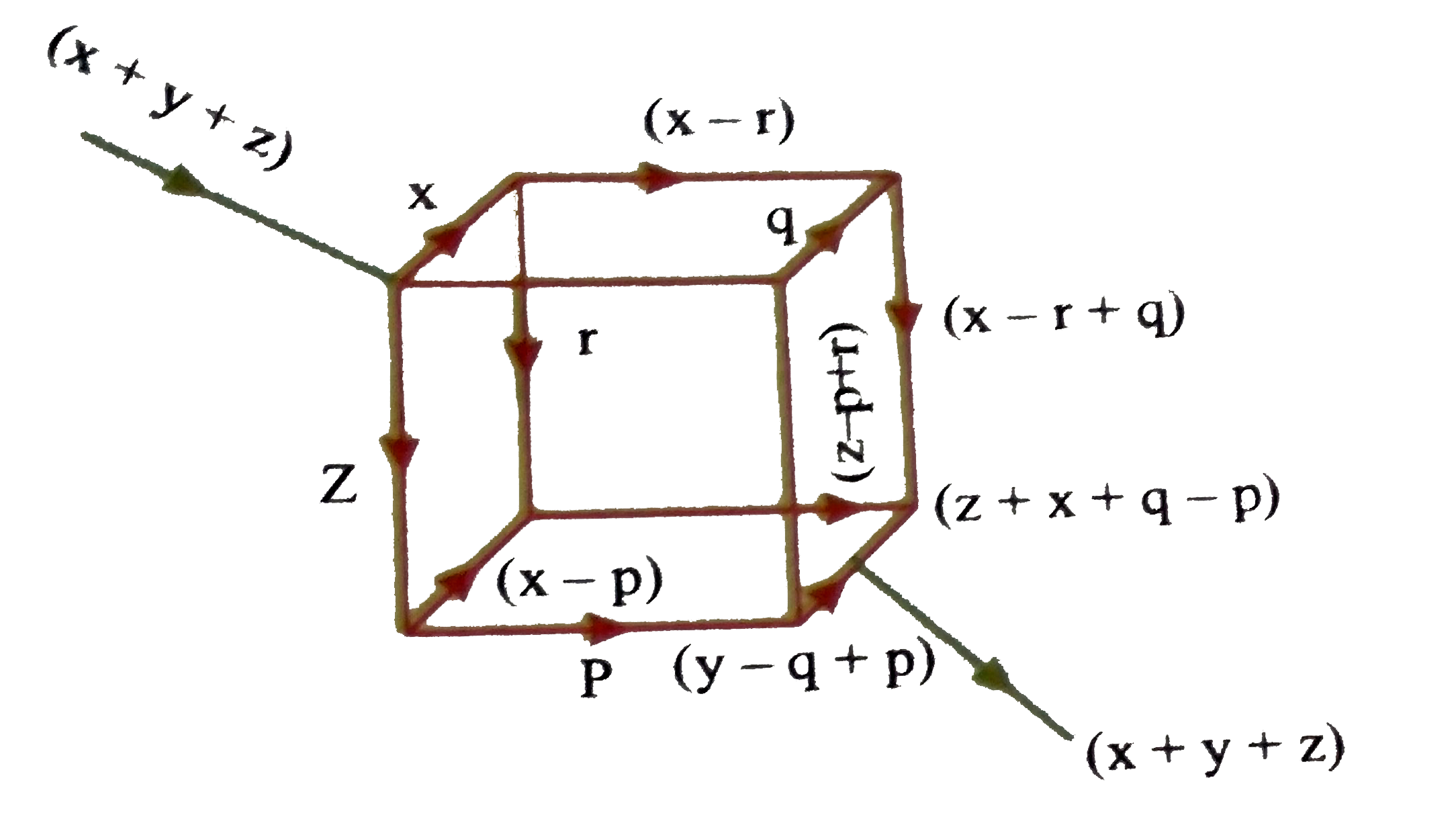
Ry+R(y−q)−RP−RZ=0 (or)
2y−Z=p+q ..(i)
Rx+Rr−R(z−p)−RZ=0 (or)
2z−x=r+P .(ii)
Ry+Rq−R(x−R)−Rx=0 (or)
2x−y=q+r ..(iii)
Therefore 2p=3y+z−3x ..(iv)
2q=3x+y−3z ..(v)
2r=3z+x−3y ..(vi)
Again (x−r)+(x−r+q)=r+(z−p+r)
(or) 2x−z=4r−p−q ..(vii)
substituting values of p,q,r, we find z=y ..(viii)
again
=(z−p)+(z−p+r)+K(z+x+q−p)
=p+(1−K)(y−q+p)
this gives K(2y+x)+8(x−y)=0 (or)
V=R[x+(x−r)+(x−r+q)+K(z+x+q−p)]
V=R[7x−2y2+2K(2x−)] ..(10)
I=x+2y ..(11)
Vi=Req=R[(7x−2y)+4K(2x−y)2(x+2y)]
=R12[10+4K−5K2]
R is maximum when K=25 and Rmax=9R10
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 5
42 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
Twelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
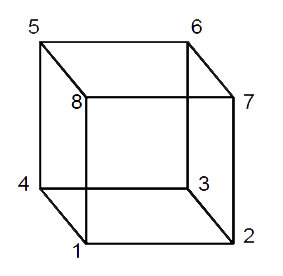
When current enters at 1 and leaves at 2
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
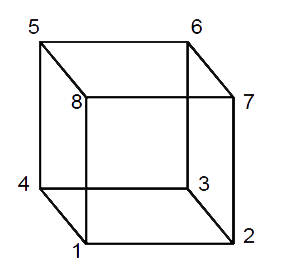
When current enters at 1 and leaves at 3
View Solution
Knowledge Check
Twelve straight uniform wires of length a and resistance R are joined to form the edges of a cube of side a. Current enters the system at one corner andd leaves from a point on one of the edges meeting at the opposite corner at a distance Ka(<K<1) from it.
Q. The maximum value of the equivalent resistance isA9R5B9R2C9R10D5R12Twelve wires each of resistance 6Ω are connected to from a cube as shown in the adjoining figure. The current enters at a cornet A and leaves at erhe diagonally opposite corner G. The equivalent resistance across the corners A and G is
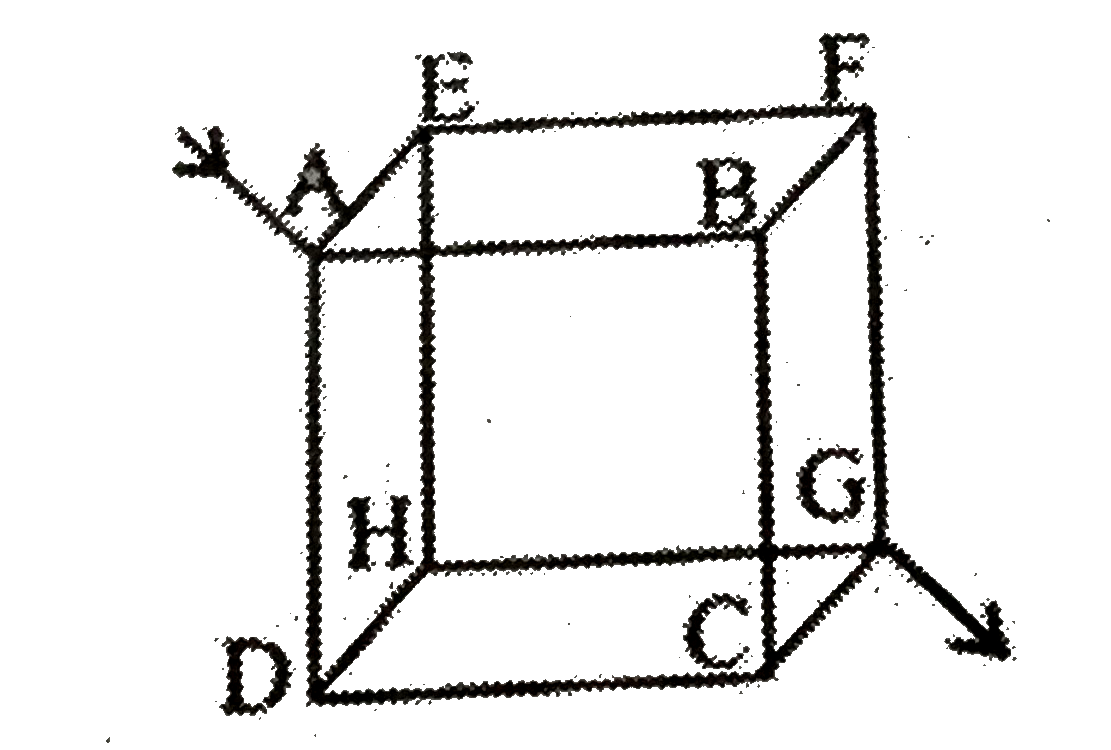 A12ΩB6ΩC3ΩD5Ω
A12ΩB6ΩC3ΩD5ΩSix wires, each of resistance r, are connected so as to form a tetrahedron. The equivalent resistance of the combination when current enters through one corner and leaves through some other corner is
ArB2rCr3Dr2
Twelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View SolutionA regular hexagon is formed by six wires each of resistance rΩ and the corners are joined to the center by wires of the same resistance. If the current enters at one corner and leaves at the opposite corner, find the equivalent resistance of the conductor.
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
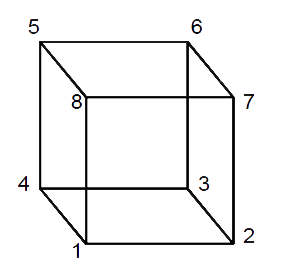
When current enters at 1 & leaves at 6 (body diagonal)
View SolutionIf the edge length of the side of a cube is a, the distance between the body centred atom and one corner atom in the cube will be:
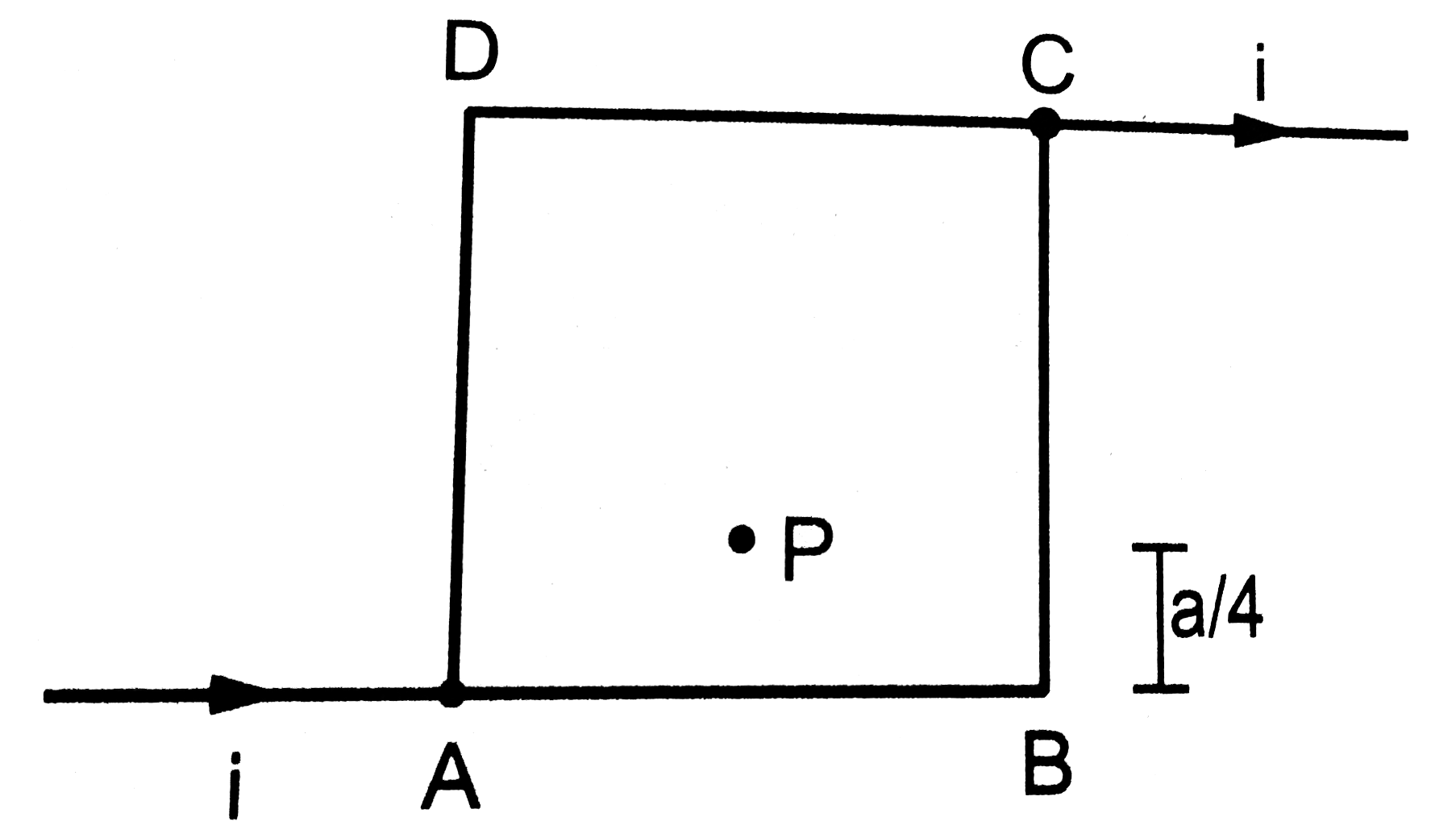
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View Solution
