Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in figure.

R12(10+4K−5K2)
R6(10+4K−5K2)
R12(5+2K−5K2)
R6(5+2K−5K2)
The correct Answer is:A
70Ω
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 542videos
CURRENT ELECTRICITY
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
- BOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.
 View Solution
View SolutionTweleve indentical resistor are arranged on all edfges of a cube. Then find the equivalent resistance between the corners 1 and 6 as shwon in fig 5.126(us nodal method)
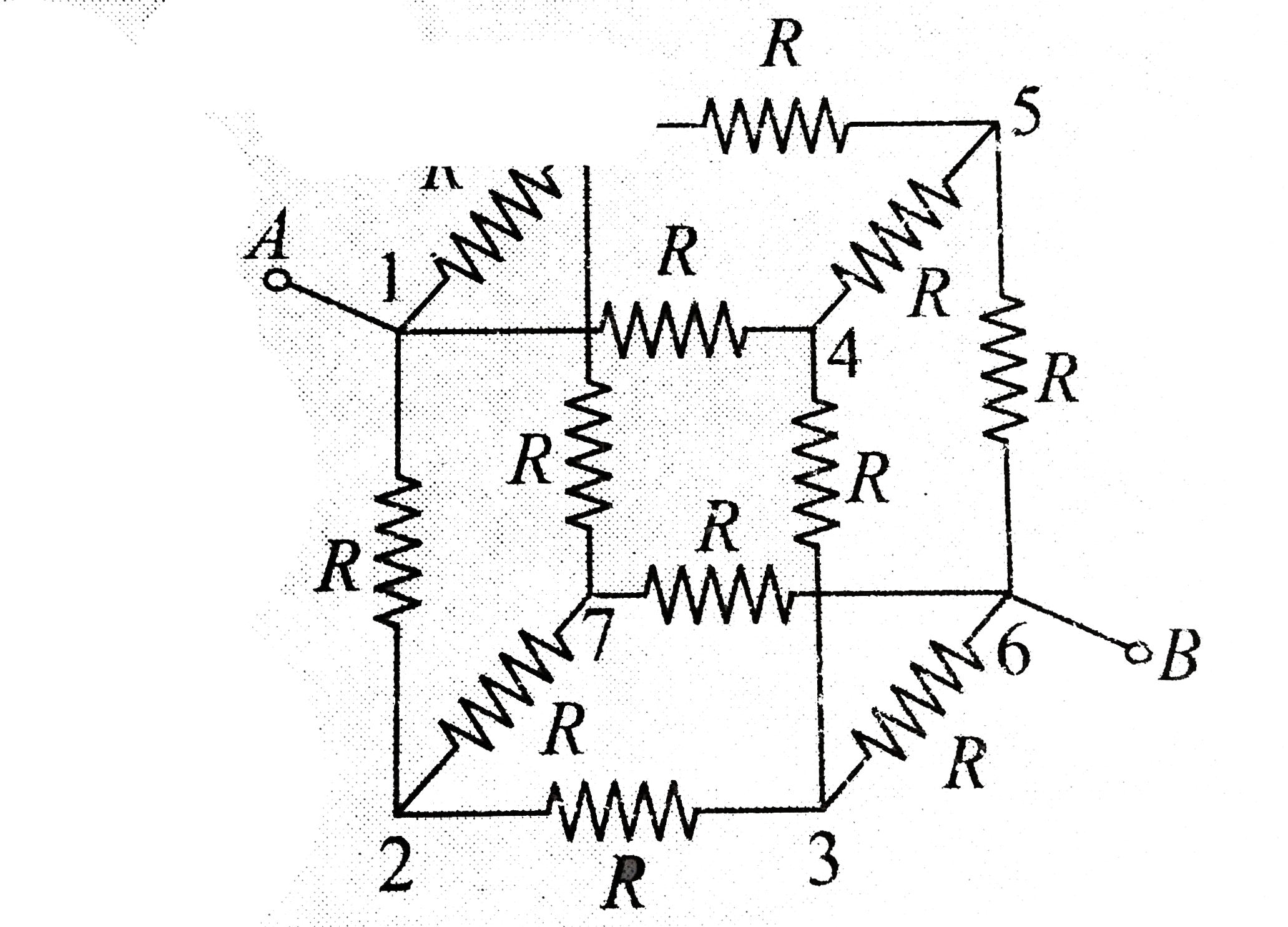 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The equivalent resistance between A and B for the mesh shown in the figure is
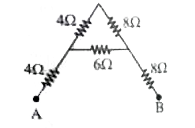 A16ΩB30ΩC4.8ΩD7.2Ω
A16ΩB30ΩC4.8ΩD7.2Ω - Question 2 - Select One
Find the equivalent resistance between A and B in the given figure.
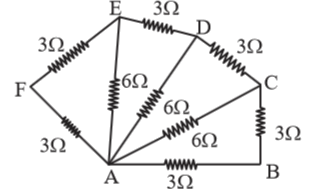 A18ΩB2ΩC9ΩD6Ω
A18ΩB2ΩC9ΩD6Ω - Question 3 - Select One
Find the equivalent resistance between the point a and b of the network shown in figure.
 A3B2C1D5
A3B2C1D5
Find the equivalent resistance between the point a and b of the circuit shown in figure
View SolutionFind the equivalent resistance between point a and b in the network shown in figure.
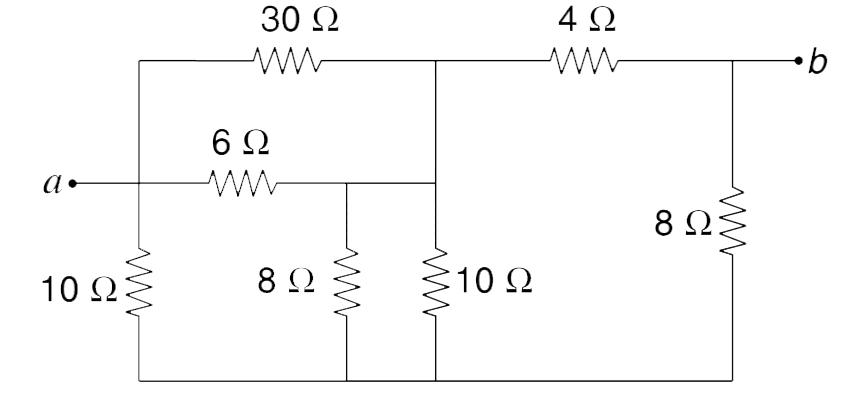 View Solution
View SolutionFind the equivalent resistance between A and B in the give figure .
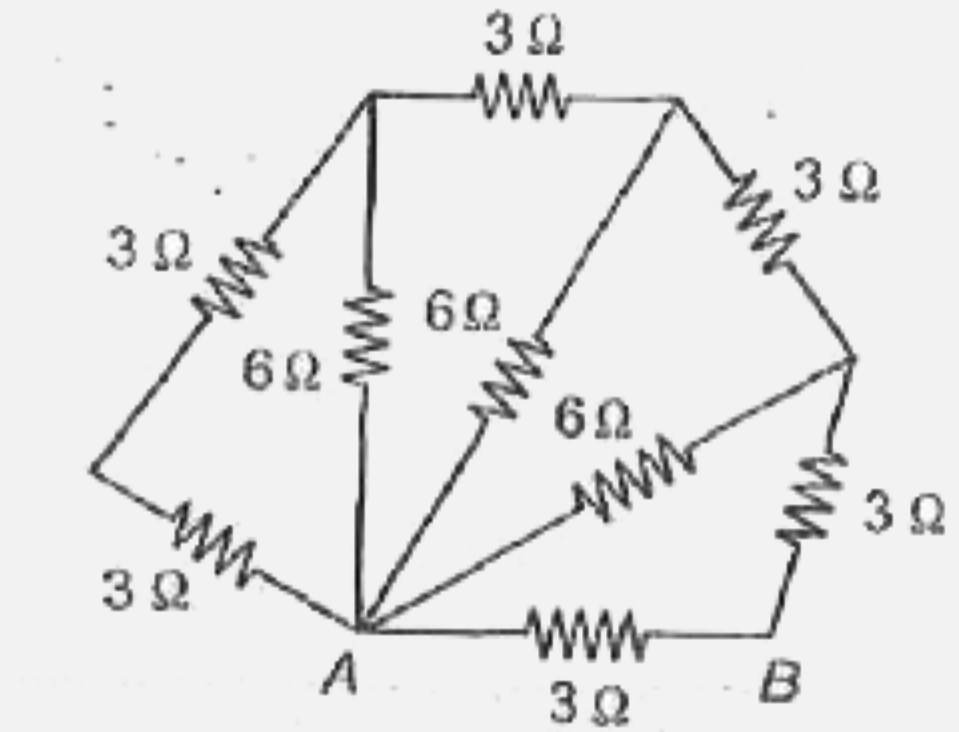 View Solution
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
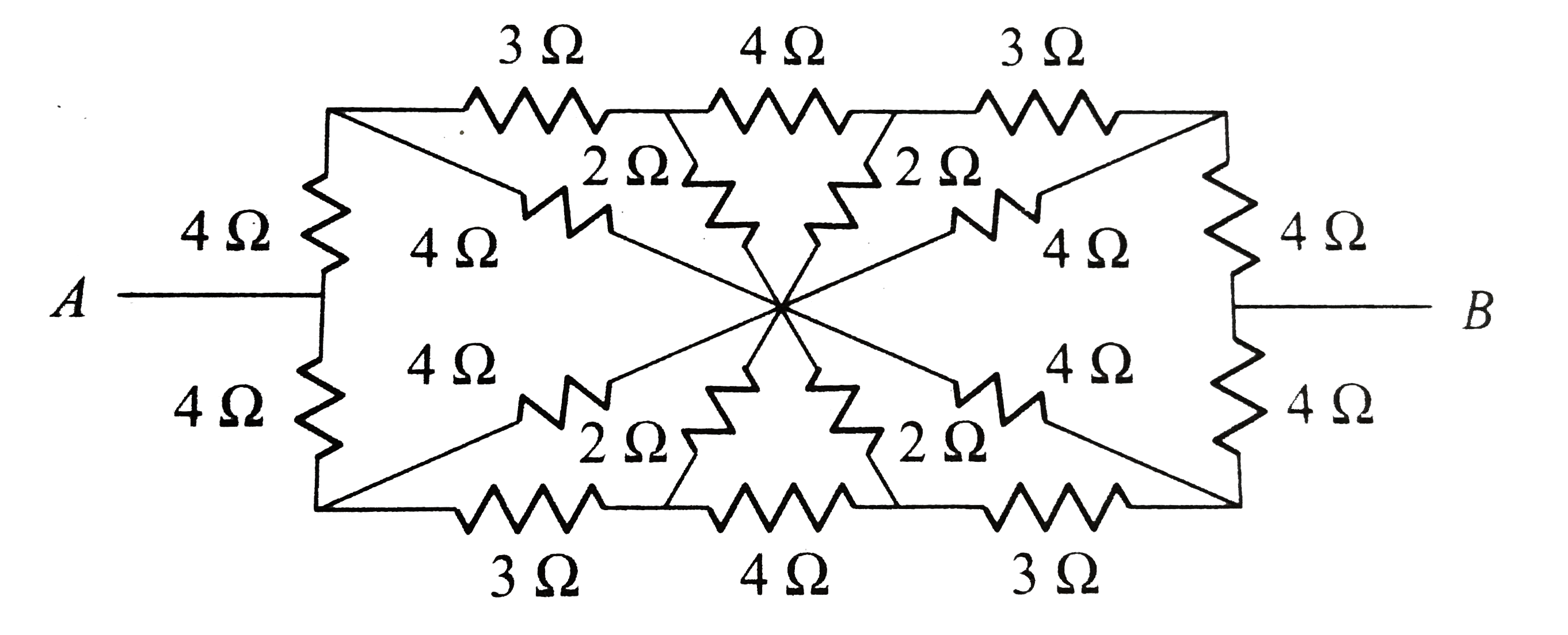 View Solution
View SolutionThe equivalent resistance resistance between A and B of network shown in figure is
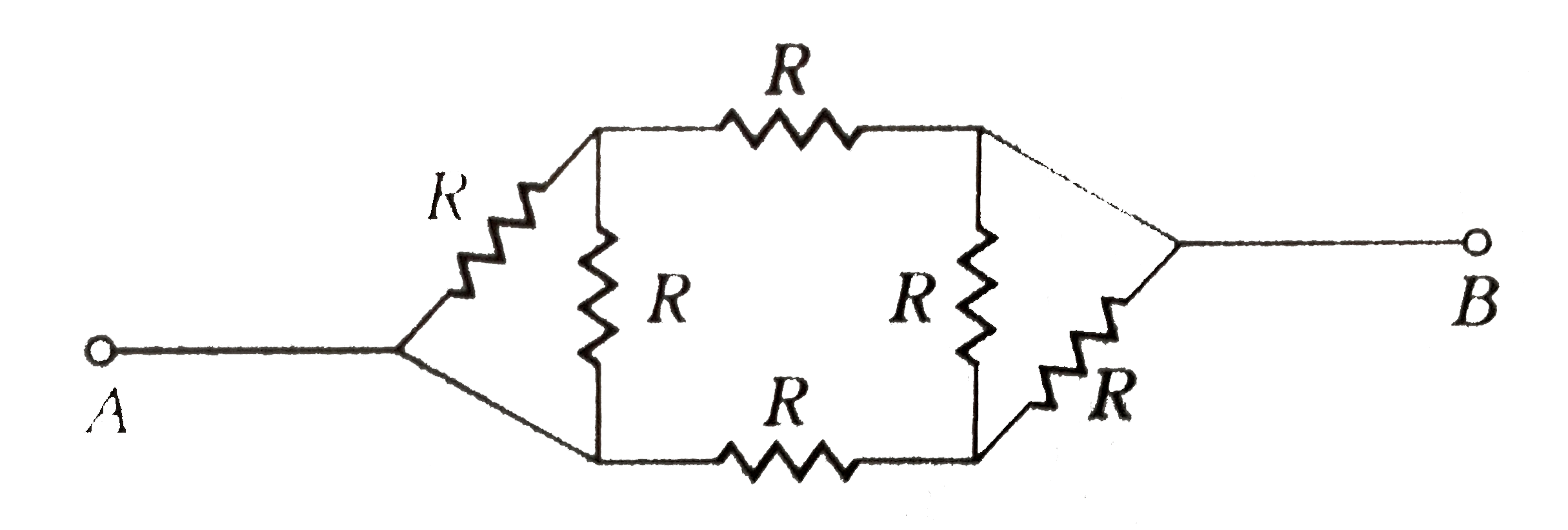 View Solution
View Solution

