In YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

Fringe width on the screen is
0.4 mm
0.1 mm
0.2 mm
0.3 mm
β=λDn2d=3000×10−10×1×23×1×10−3=2×10−4m=0.2m
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionTwo coherent point sources S_1 and S_2 are separated by a small distance d as shown. The fringes obtained on the screen will be
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S_1 and S_2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S_1 and S_2 medium of refractive index n_1 = 2 is present and to the right of S_1 and S_2 medium of n_2 = 3/2 , is present. A thin slab of thickness 't' is placed in front of S_1 . The refractive index of n_3 of the slab varies with distance from it's starting face as shown in figure. If thickness of the slab is selected 1 mum , then position of central maxima will be : (y-coordinate)
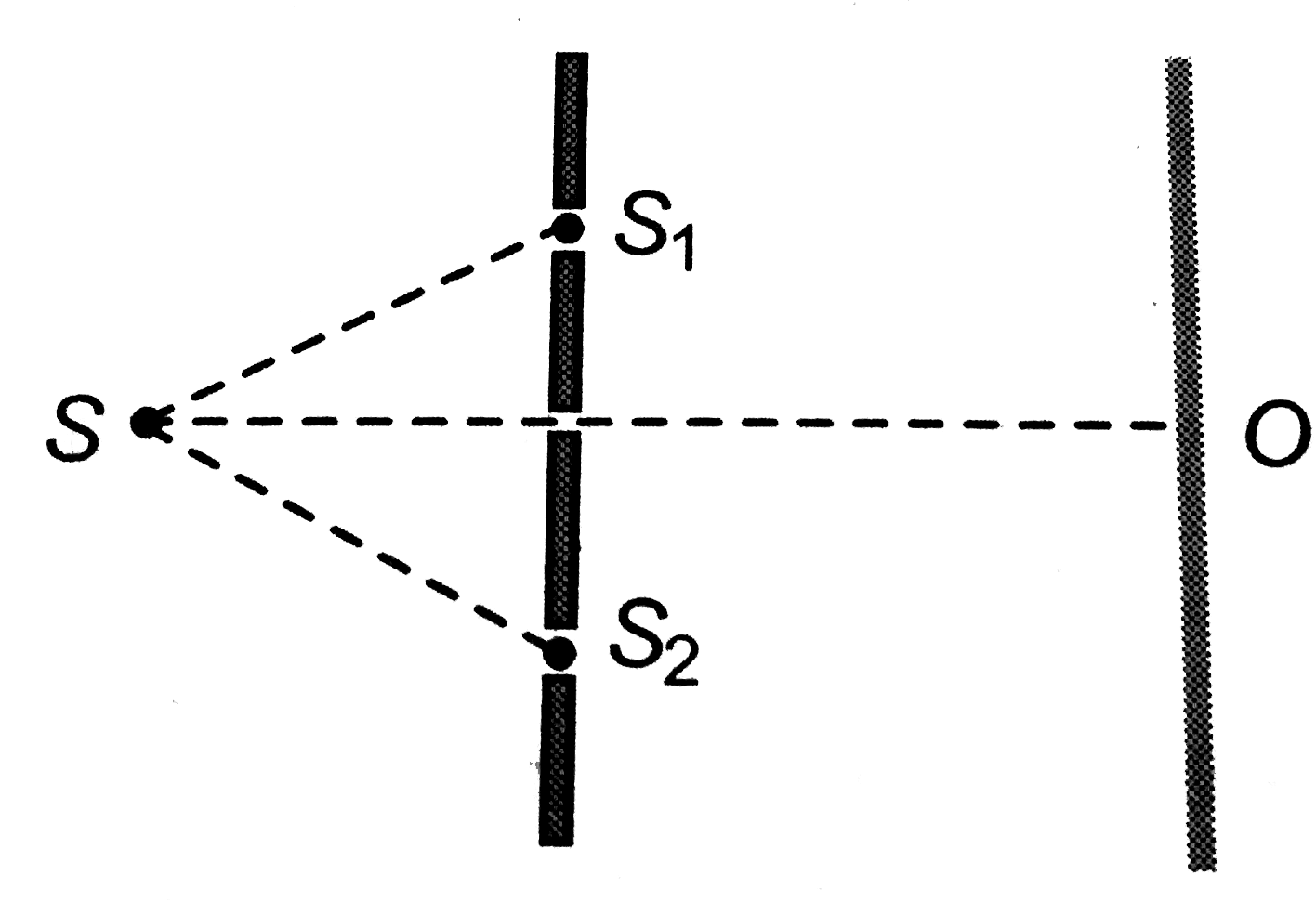
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View SolutionIf S1,S2 and S3 denote the sum of first n1,n2 and n3 terms respectively of an A.P. Then S1n1(n2−n3)+S2n2(n3−n1)+S3n3(n1−n2) equals :
View SolutionIn young's double slit experiment, distance between the slit S_1 and S_2 is d and the distance between slit and screen is D . Then longest wavelength that will be missing on the screen in front of S_1 is
View SolutionTwo coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View Solutionयंग के द्विस्लिट प्रयोग में, माना S1 व S2 दो स्लिटें हैं तथा C परदे का केन्द्र है। यदि ∠S1CS2=θ तथा λ तरंगदैर्ध्य है, फ्रिन्जों की चौड़ाई होगी
View SolutionTwo connected point sources S_1 And S_2 Are distant from each other by a short distance 'd as shown in the figure. Fringe seen on screen
View Solutionदो कलासम्बद्ध बिन्दु स्त्रोत S1 एवं S2 एक लघु दूरी 'd द्वारा एक दूसरे से दूर हैं जैसा कि चित्र में दर्शाया गया है। पर्दे पर देखी गई फ्रिन्जें हैं
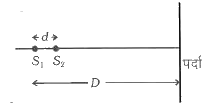
View SolutionTwo coherent point sources S_1 and S_2 are separated by a small distance d as shown. The fringes obtained on the screen will be
View SolutionTwo coherent point sources S_1 and S_2 are separated by a small distance d as shown. The fringes obtained on the screen will be
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then

View Solution
