In parallelogram ABCD, E is mid-point of CD and through D, a line is drawr parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that:
2×AD=GC
To prove that 2×AD=GC in parallelogram ABCD, where E is the midpoint of CD, and a line through D is drawn parallel to EB meeting CB produced at point G and cutting AB at point F, we can follow these steps:
1. Identify the Properties of the Parallelogram:
Since ABCD is a parallelogram, we know that:
AD=BCandAB=CD
2. Use the Midpoint Theorem:
Since E is the midpoint of CD, we can apply the midpoint theorem. The theorem states that if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half as long.
- Here, EB is parallel to DG and E is the midpoint of CD.
3. Apply the Reverse of the Midpoint Theorem:
According to the reverse of the midpoint theorem, if EB is parallel to DG, then B must be the midpoint of CG.
- Therefore, we can conclude:
BG=GC
4. Express GC in Terms of BC:
Since B is the midpoint of CG, we can express GC as:
GC=2×BG
And since BG=BC (because B is the midpoint), we have:
GC=2×BC
5. Substitute BC with AD:
From the properties of the parallelogram, we know that:
BC=AD
Substituting this into our equation gives:
GC=2×AD
6. Conclusion:
Thus, we have shown that:
2×AD=GC
This completes the proof.
Since ABCD is a parallelogram, we know that:
AD=BCandAB=CD
Since E is the midpoint of CD, we can apply the midpoint theorem. The theorem states that if a line segment connects the midpoints of two sides of a triangle, it is parallel to the third side and half as long.
- Here, EB is parallel to DG and E is the midpoint of CD.
According to the reverse of the midpoint theorem, if EB is parallel to DG, then B must be the midpoint of CG.
- Therefore, we can conclude:
BG=GC
Since B is the midpoint of CG, we can express GC as:
GC=2×BG
And since BG=BC (because B is the midpoint), we have:
GC=2×BC
From the properties of the parallelogram, we know that:
BC=AD
Substituting this into our equation gives:
GC=2×AD
Thus, we have shown that:
2×AD=GC
This completes the proof.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:PYTHAGORAS THEOREM
Explore 5 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:RECTILINEAR FIGURES
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:INEQUALITIES
Explore 7 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
In parallelogram ABCD, E is mid-point of CD and through D, a line is drawn parallel to EB to meet CB produced at point G and to cut AB at point F. Prove that :
DG = 2EB
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
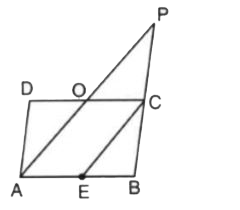
PB=2AD
View SolutionIn parallelogram PQRS. L is mid-point of side Sr and SN is drawn parallel to LQ which meets RQ produced prove that :
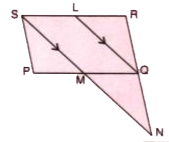
SN=2LQ
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
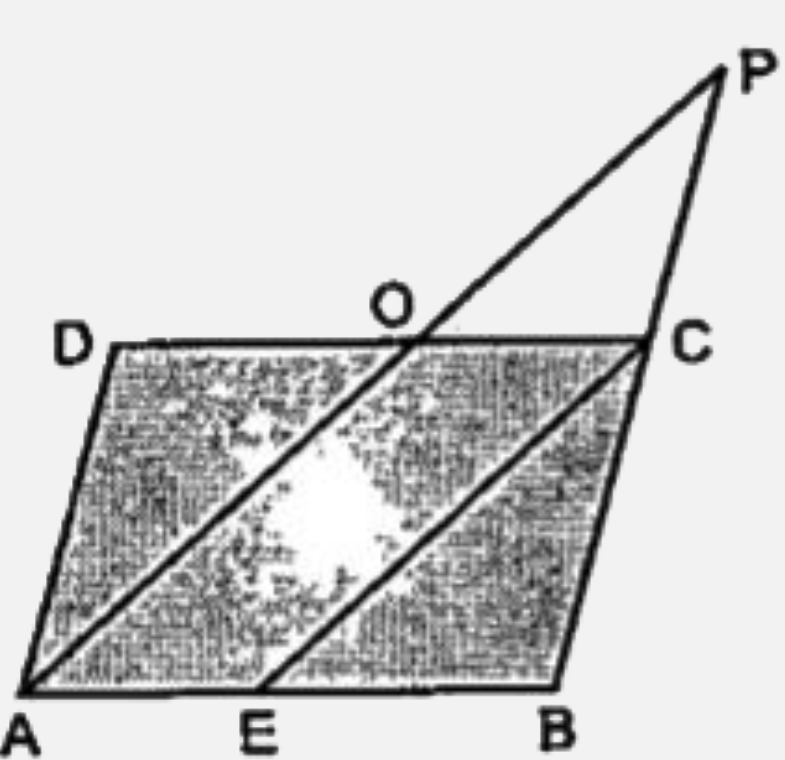
BP=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.
View SolutionIn parallelogram PQRS. L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced prove that :
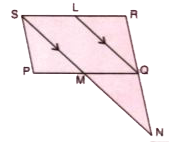
SP=12RN
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View Solution