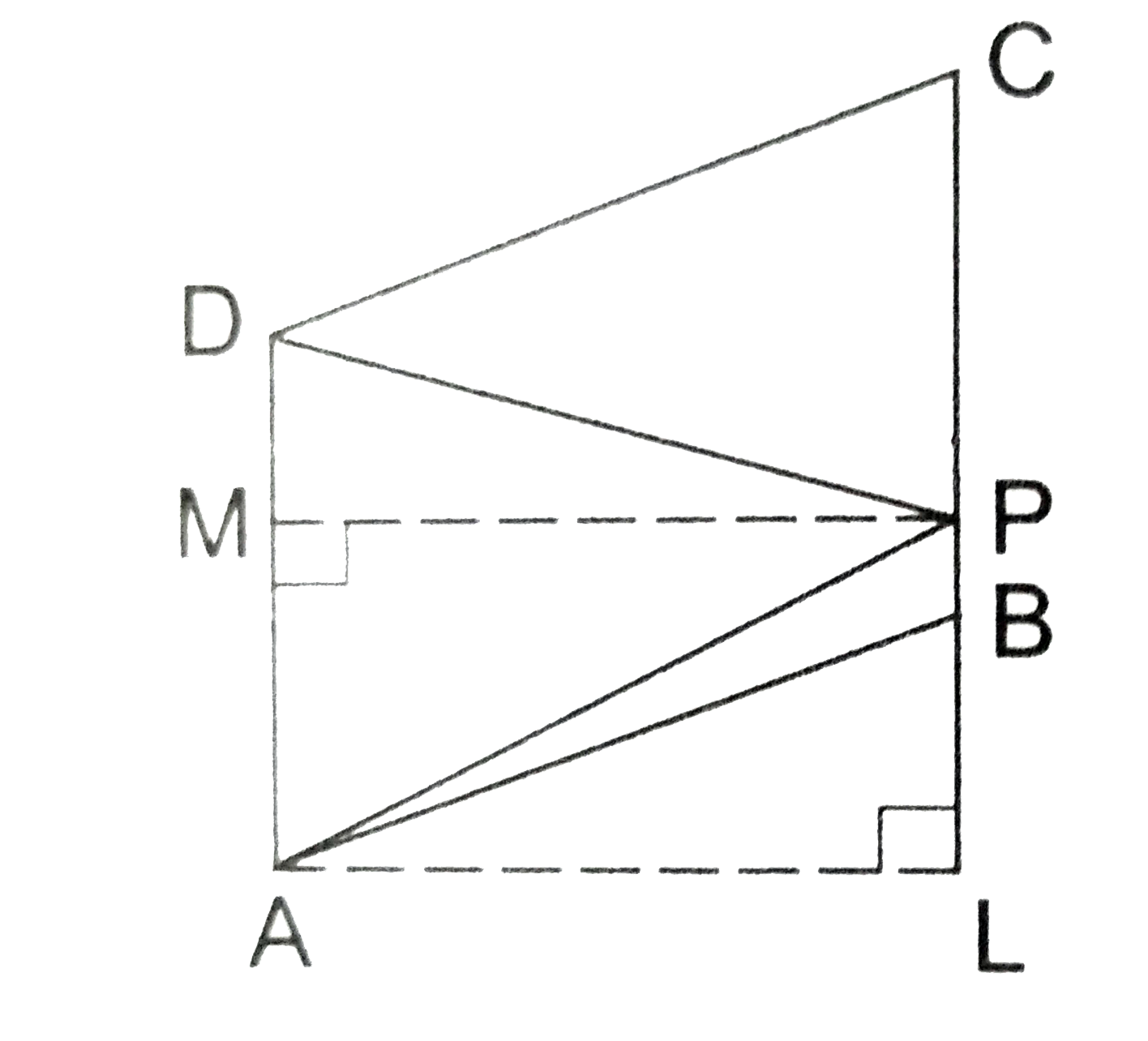
In the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that ar(△ABP)=ar(qaud. ABCD).
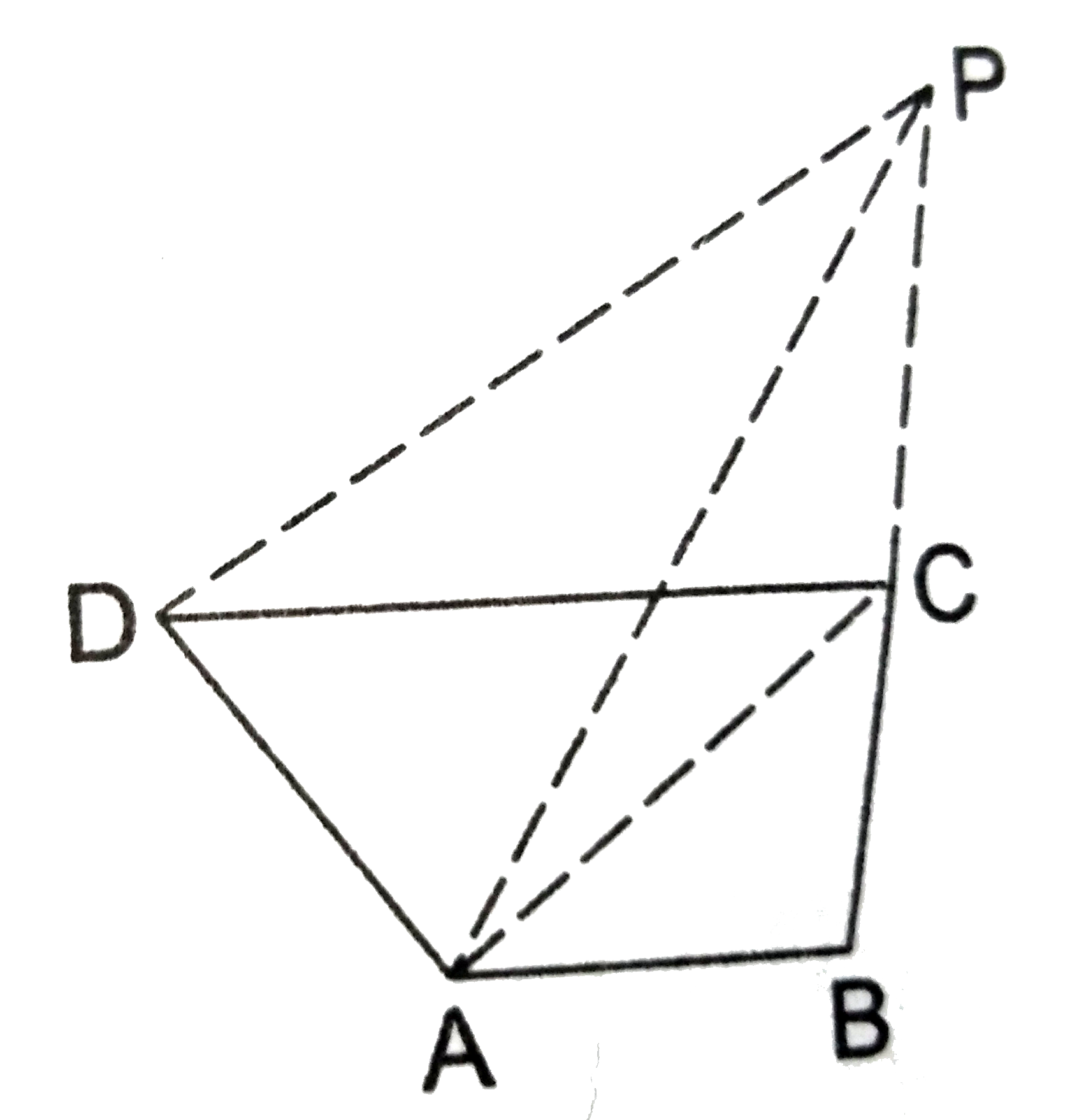
△ACDand△ACP are on the same basea and between the same parallels.
∴ar(△ACP)=ar(△ACD)
⇒ar(△ACP)+ar(△ABC)=ar(△ACD)+ar(△ABC).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In the adjoining figure, the area of quadrilateral ABCD is
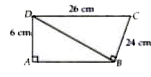 A148 cm2B144cm2C120 cm2D122 cm2
A148 cm2B144cm2C120 cm2D122 cm2In the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
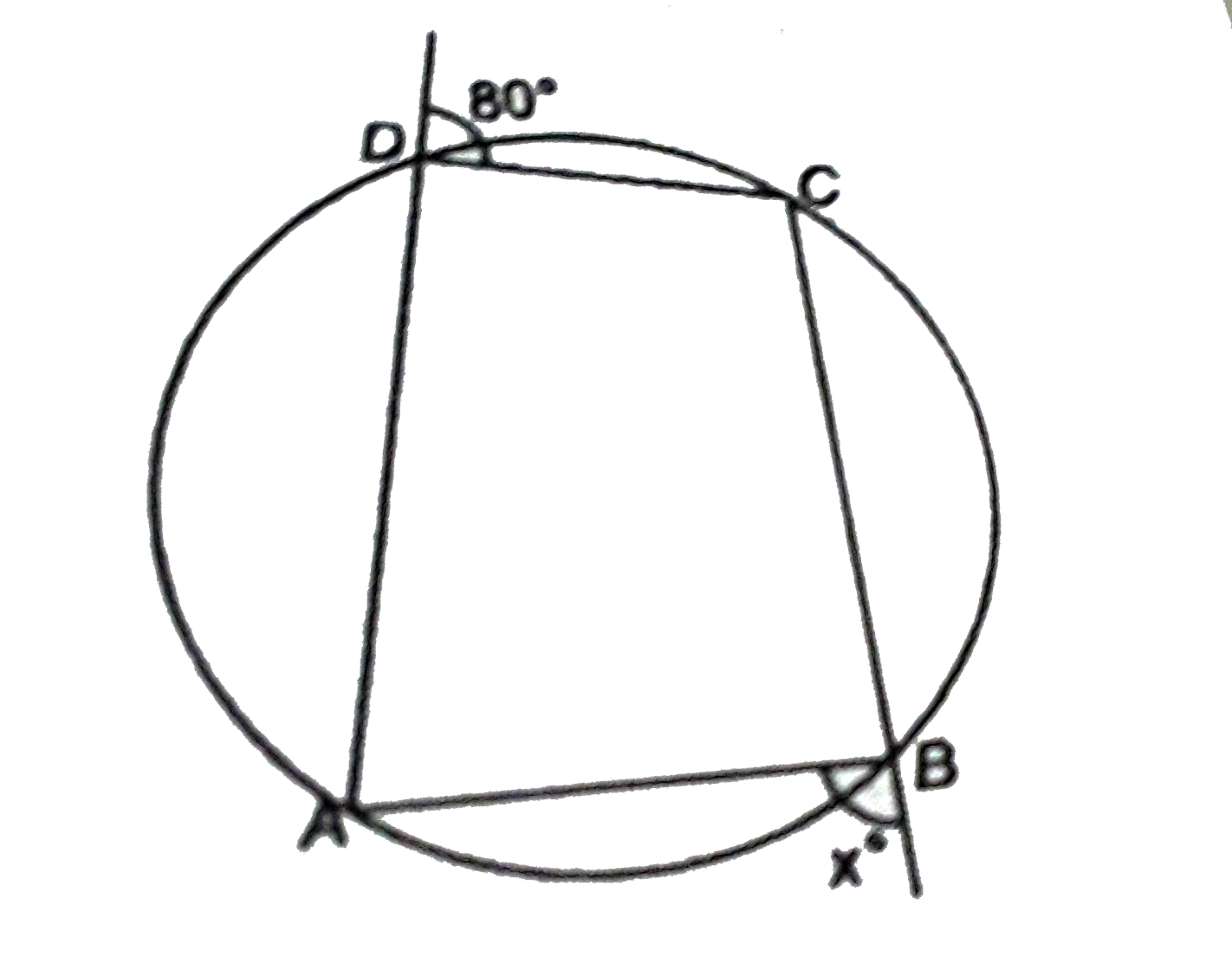 A60∘B80∘C100∘D120∘
A60∘B80∘C100∘D120∘
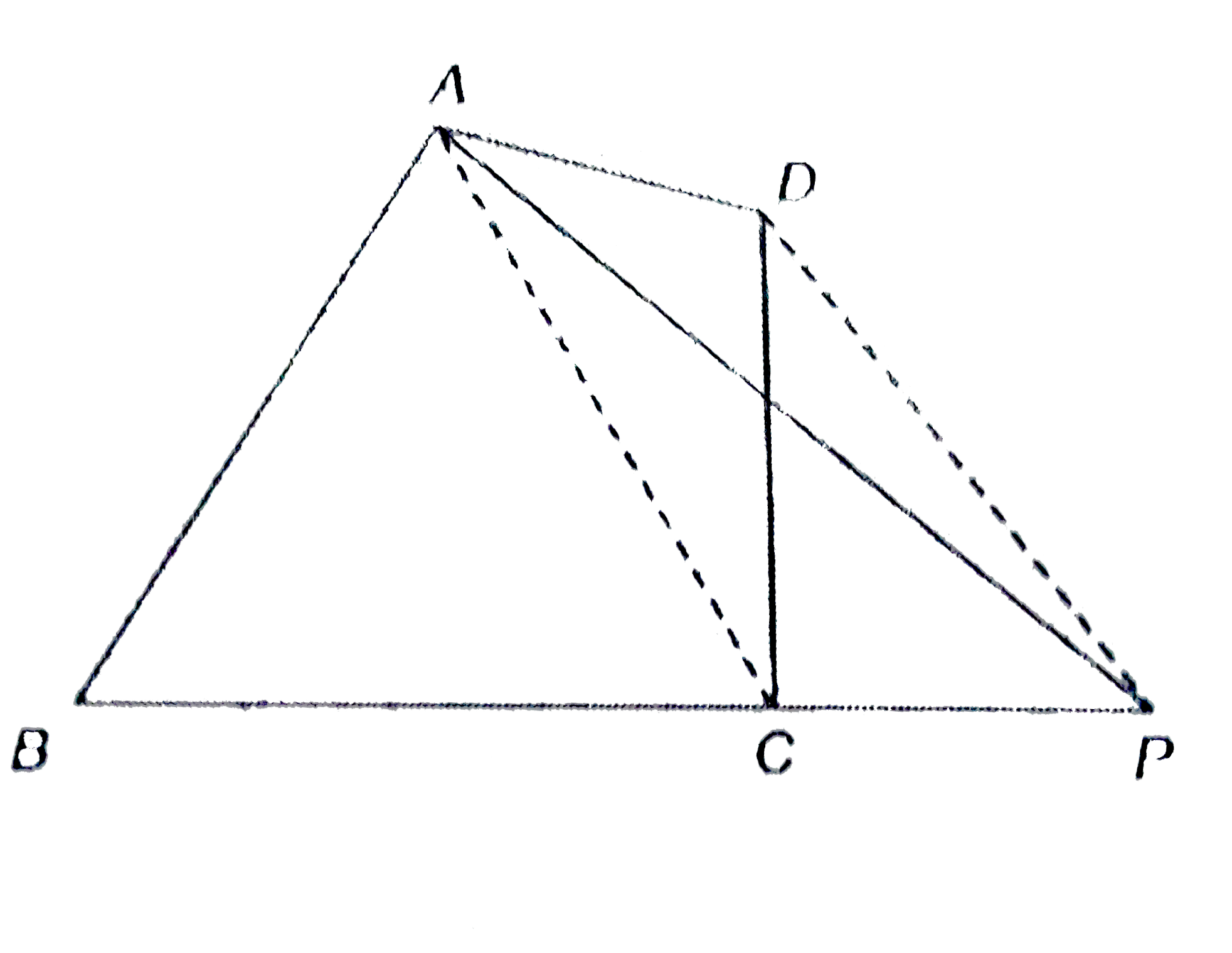
In the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
area of ΔABP= area of □ABCD
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
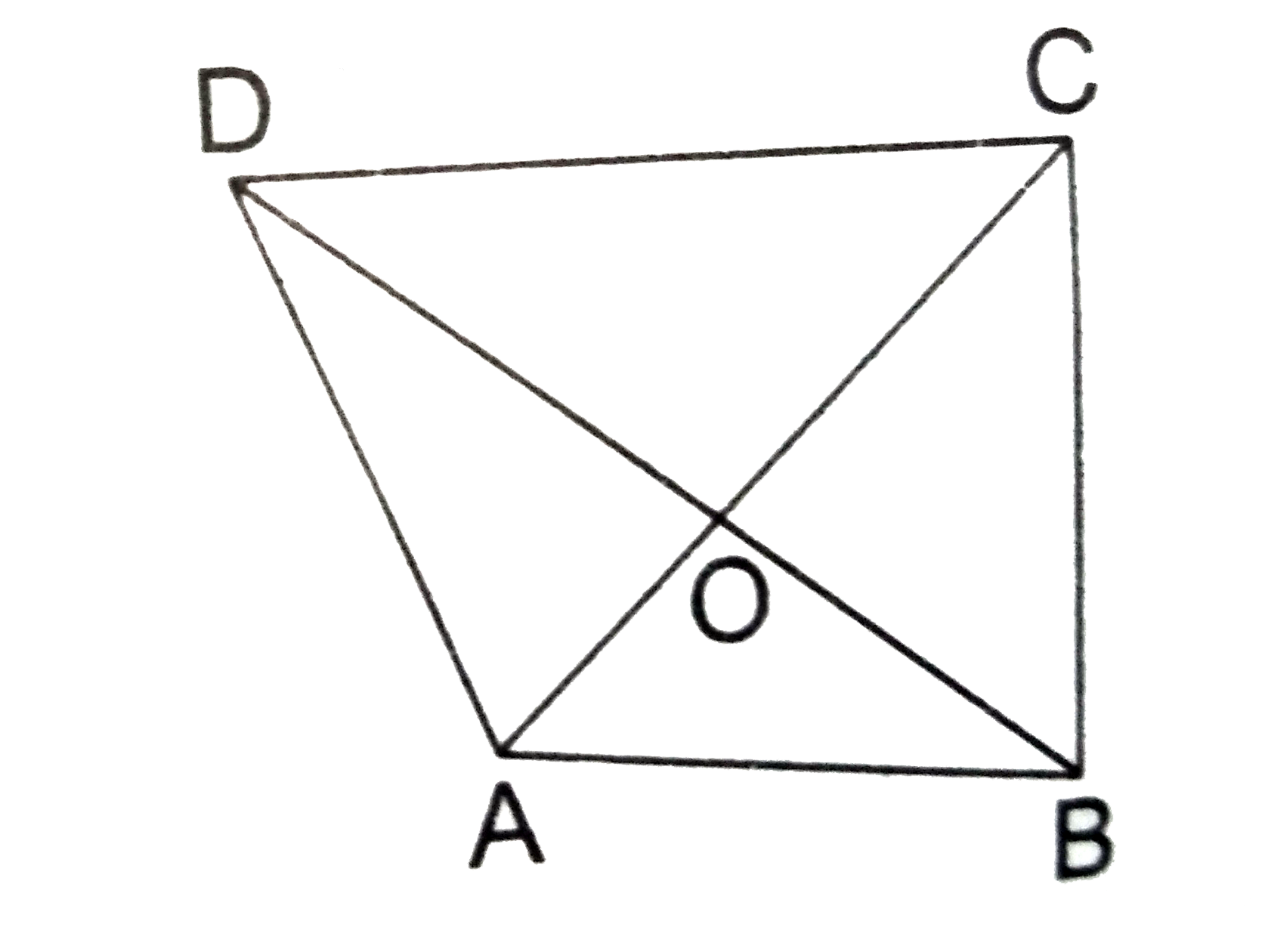
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View SolutionABCD is a quadrilateral. The straight line through C parallel to the diagonal DB intersects AB produced at E. Prove that the ar(quad. ABCD) = ar(△ADE).

View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).

View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View Solution
