If the sum of the two adjacent angles is 180∘; then their non-common arms are two oppposite rays.
To prove the theorem that states if the sum of two adjacent angles is 180∘, then their non-common arms are two opposite rays, we can follow these steps:
1. Identify the Given Information:
- Let the two adjacent angles be ∠ACD and ∠BCD.
- We know that ∠ACD+∠BCD=180∘.
2. Understand the Definition of Adjacent Angles:
- Adjacent angles are angles that share a common vertex and a common arm but do not overlap.
- In this case, the common arm is CD and the common vertex is C.
3. Assume the Opposite:
- To prove the theorem, we will assume that the non-common arms CA and CB are not opposite rays.
- If CA and CB are not opposite rays, we can draw another ray CE which is opposite to ray CA.
4. Construct the Ray:
- Draw ray CE such that A,C,E are collinear, meaning A, C, and E lie on a straight line.
5. Apply the Straight Angle Property:
- Since CD stands on the line ACE, we have:
∠ACD+∠ECD=180∘
6. Use the Given Condition:
- From the given information, we know:
∠ACD+∠BCD=180∘
7. Set Up the Equation:
- Since both ∠ACD+∠ECD and ∠ACD+∠BCD equal 180∘, we can equate them:
∠ACD+∠ECD=∠ACD+∠BCD
8. Subtract ∠ACD from Both Sides:
- By subtracting ∠ACD from both sides, we get:
∠ECD=∠BCD
9. Analyze the Position of Rays:
- Since CE and CB are on the same side of CD and ECD equals BCD, it implies that rays CE and CB must coincide.
10. Conclude the Proof:
- This leads to a contradiction because we assumed that CA and CB were not opposite rays. Therefore, our assumption must be incorrect.
- Hence, we conclude that CA and CB are indeed opposite rays.
Final Statement
Thus, we have proved that if the sum of two adjacent angles is 180∘, then their non-common arms are two opposite rays.
- Let the two adjacent angles be ∠ACD and ∠BCD.
- We know that ∠ACD+∠BCD=180∘.
- Adjacent angles are angles that share a common vertex and a common arm but do not overlap.
- In this case, the common arm is CD and the common vertex is C.
- To prove the theorem, we will assume that the non-common arms CA and CB are not opposite rays.
- If CA and CB are not opposite rays, we can draw another ray CE which is opposite to ray CA.
- Draw ray CE such that A,C,E are collinear, meaning A, C, and E lie on a straight line.
- Since CD stands on the line ACE, we have:
∠ACD+∠ECD=180∘
- From the given information, we know:
∠ACD+∠BCD=180∘
- Since both ∠ACD+∠ECD and ∠ACD+∠BCD equal 180∘, we can equate them:
∠ACD+∠ECD=∠ACD+∠BCD
- By subtracting ∠ACD from both sides, we get:
∠ECD=∠BCD
- Since CE and CB are on the same side of CD and ECD equals BCD, it implies that rays CE and CB must coincide.
- This leads to a contradiction because we assumed that CA and CB were not opposite rays. Therefore, our assumption must be incorrect.
- Hence, we conclude that CA and CB are indeed opposite rays.
Thus, we have proved that if the sum of two adjacent angles is 180∘, then their non-common arms are two opposite rays.
Similar Questions
If the sum of two adjacent angles is 180∘, then the ___ arms of the two angles are opposite rays.
View SolutionIn a rhombus, the sum of adjacent angles is
View SolutionFill in the blanks so as to make the following statements true: (i) If one angle of a linear pair is acute, then its other angle will be .......... (ii) A ray stands on a line, then the sum of the two adjacent angles so formed is .................. (iii) If the sum of two adjacent angles is 180∘, then the ............ arms of the two angles are opposite rays.
View SolutionLINEAR PAIR Two adjacents angles are said to form a linear pair of angles if their non-common arms are two opposite rays.
View SolutionIn a parallelogram the sum of any two adjacent angles is 1800.
View SolutionAssertion : The value of x in the following figure is 40°.
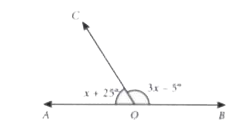
Reason: A linear pair is a pair of adjacent angles whose non-common arms are opposite rays.
View SolutionThe sum of the three angles of a triangle is 180∘
View SolutionRead the following two statements which are taken as axiom:
(i) If two lines intersect each other , then the vertically opposite angles are not equal.
(ii) If a ray stands on a line , then the sum of two adjacent angles, so formed is equal to 180∘.
Is this system of axioms consistent ? Justify your answer.
View SolutionIf the sum of two angles is greater than 180∘, then which of the following is not possible for the two angles ?
View SolutionThe sum of adjacent angles of a parallelogram is
View Solution
