Assertion : The value of x in the following figure is 40°.
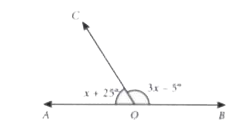
Reason: A linear pair is a pair of adjacent angles whose non-common arms are opposite rays.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If assertion is false but reason is true.
Step by step video & image solution for Assertion : The value of x in the following figure is 40°. Reason: A linear pair is a pair of adjacent angles whose non-common arms are opposite rays. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If a & b forms a pair of adjacent angles then which figures proves it .
A
B
C
D
- Question 2 - Select One
Which of the following pairs of angles are not adjacent angles?
A∠AOB,∠BODB∠BOC,∠AOCC∠COD,∠AOCD∠BOC,∠AOB - Question 3 - Select One
Which of the following options is correct :-
A pair of adjacent angles have.
(i)Common vertex
(ii)Common Arm.
(iii)Non Common arms are an opposite sides of common arms.
(iv)Non Common arms are on the same side of common arms.A(i) & (ii) are sufficientB(i),(ii) & (iii) are sufficientC(i) ,(ii) & (iv) are sufficientDAll are sufficient
LINEAR PAIR Two adjacents angles are said to form a linear pair of angles if their non-common arms are two opposite rays.
View SolutionName the pairs of adjacent angles in the figures given below :
View SolutionIn Fig.24, write all pairs of adjacent angles and all the linear pairs.
View SolutionWrite down each pair of adjacent angles shown in the following figures:
View SolutionHow many pairs of adjacent angles, in all, can you name in Figure.
View Solution