The angle subtended by an arc of a circle at the centre is double the angle subtended by it any point on the remaining part of the circle.
To prove that the angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle, we will consider two cases: when the arc is a minor arc and when it is a major arc.
Step 1: Define the Circle and Angles
- Let O be the center of the circle.
- Let P and Q be the endpoints of the arc PQ.
- Let A be any point on the remaining part of the circle.
- We need to prove that ∠POQ=2×∠PAQ.
Step 2: Case 1 - Minor Arc
- In the case where PQ is a minor arc, extend line OA to point B such that B lies outside the circle.
- The angles we are interested in are ∠POQ at the center and ∠PAQ at point A.
Step 3: Use Isosceles Triangle Properties
- Since OP=OQ=r (the radius of the circle), triangle OAP is isosceles.
- Therefore, ∠OAP=∠OPA.
Step 4: Apply the Exterior Angle Theorem
- According to the exterior angle theorem, we have:
∠BOA=∠OAP+∠OPA
- Since ∠OAP=∠OPA, we can write:
∠BOA=2×∠OAP
Step 5: Relate Angles
- The angle ∠BOA is equal to ∠POQ since they subtend the same arc.
- Thus, we have:
∠POQ=2×∠OAP
- Since ∠PAQ=∠OAP, we conclude:
∠POQ=2×∠PAQ
Step 6: Case 2 - Major Arc
- Now consider the case where PQ is a major arc.
- Extend line OA to point D such that D lies outside the circle.
- The same reasoning applies as in the minor arc case, using the exterior angle theorem with triangles OAP and OAQ.
Step 7: Conclude for Major Arc
- By similar arguments as in the minor arc case, we can show that:
∠POQ=2×∠PAQ
Step 8: Special Case - Straight Line
- If P and Q are such that ∠POQ=180∘, then:
∠PAQ=90∘
- Thus, ∠POQ=2×90∘=180∘, which holds true.
Conclusion
In all cases (minor arc, major arc, and straight line), we have shown that:
∠POQ=2×∠PAQ
This completes the proof.
- Let O be the center of the circle.
- Let P and Q be the endpoints of the arc PQ.
- Let A be any point on the remaining part of the circle.
- We need to prove that ∠POQ=2×∠PAQ.
- In the case where PQ is a minor arc, extend line OA to point B such that B lies outside the circle.
- The angles we are interested in are ∠POQ at the center and ∠PAQ at point A.
- Since OP=OQ=r (the radius of the circle), triangle OAP is isosceles.
- Therefore, ∠OAP=∠OPA.
- According to the exterior angle theorem, we have:
∠BOA=∠OAP+∠OPA
- Since ∠OAP=∠OPA, we can write:
∠BOA=2×∠OAP
- The angle ∠BOA is equal to ∠POQ since they subtend the same arc.
- Thus, we have:
∠POQ=2×∠OAP
- Since ∠PAQ=∠OAP, we conclude:
∠POQ=2×∠PAQ
- Now consider the case where PQ is a major arc.
- Extend line OA to point D such that D lies outside the circle.
- The same reasoning applies as in the minor arc case, using the exterior angle theorem with triangles OAP and OAQ.
- By similar arguments as in the minor arc case, we can show that:
∠POQ=2×∠PAQ
- If P and Q are such that ∠POQ=180∘, then:
∠PAQ=90∘
- Thus, ∠POQ=2×90∘=180∘, which holds true.
In all cases (minor arc, major arc, and straight line), we have shown that:
∠POQ=2×∠PAQ
This completes the proof.
Similar Questions
Theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
View SolutionConsider the following statements
1. the opposite angles of a cyclic quadrilateral are supplementary.
2. Angle subtended by an arc at the centre is doubled the angle subtended by it any point on the remaining part of the circle.
Which one of the following is correct in respect of the above statements
View Solution
Knowledge Check
The total plane angle subtended by a circle at its centre is
Aπ radB2π radC2π3 radDπ2 radIf the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
A120∘B150∘C100∘D110∘
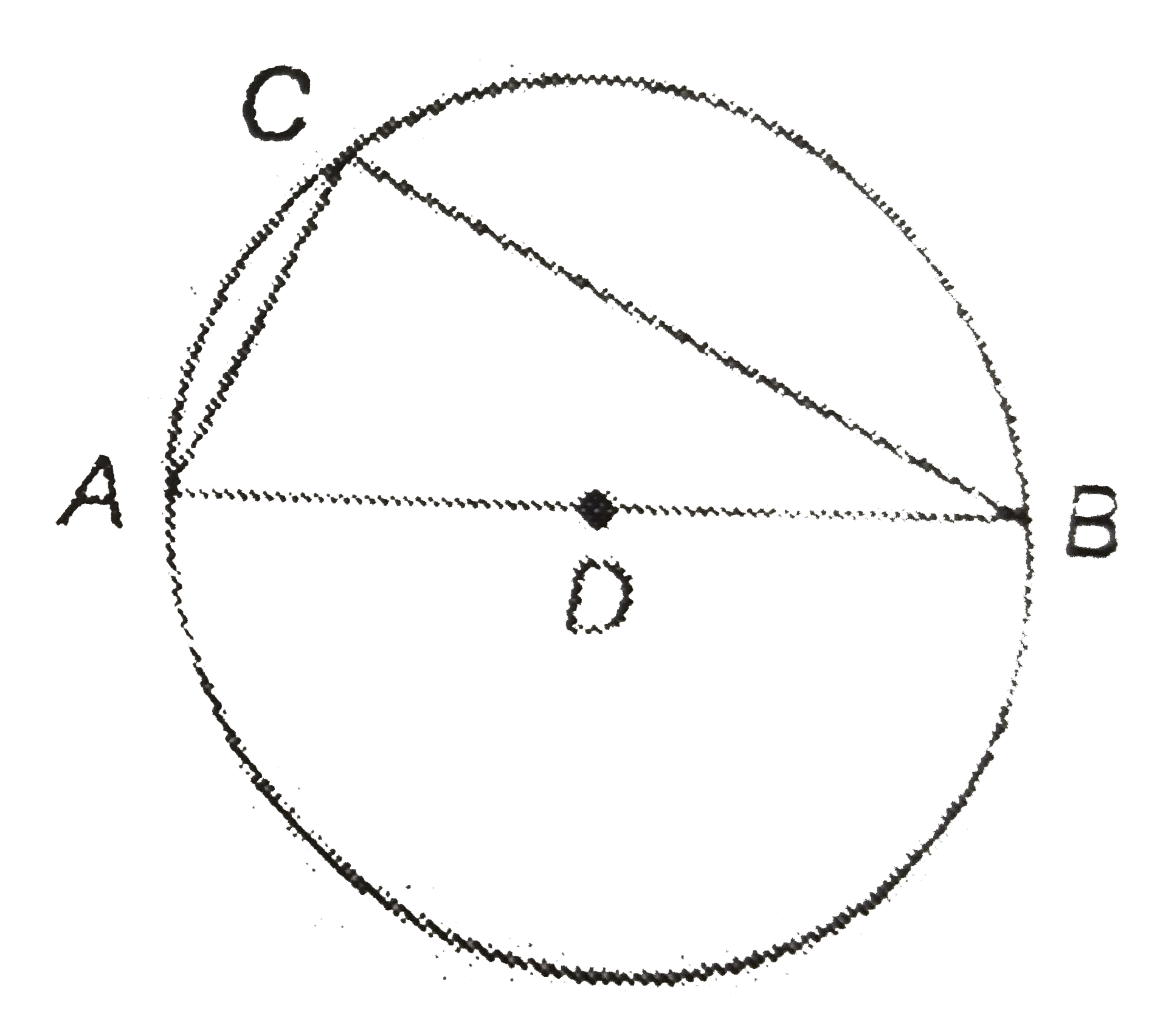
Show that any angle in a semi-circle is a right angle.
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
View SolutionTheorem:-5 (i) The degree measure of an arc or angle subtended by an arc at the centre is double the angle subtended by it at any point of alternate segment. (ii) Angle in the same segment of a circle are equal (iii) The angle in the semi circle is right angle.
View SolutionAngle subtend by an arc at center is double the angle subtend b it at any point on remaining part OF circle||Angle is a semi circle is a 90 ||Example ||Congurent arc|| Equal arc||Cyclic quadrilateral
View SolutionA piece of wire of length 33 cm is bent into an arc of a circle of radius 14 cm. What is the angle subtended by the arc at the centre of the circle ?
View SolutionThe length of a minor arc is 29 of the circumference of the circle. Write the measure of the angle (in degrees) subtended by the arc at the centre of the circle.
View SolutionGiven an are PQ of a circle subtending angles POQ at the centre PAQ at a point A on the remaining part of the circle. We need to prove that ∠POQ=2∠PAQ.
View Solution
