Consider the following statements
1. the opposite angles of a cyclic quadrilateral are supplementary.
2. Angle subtended by an arc at the centre is doubled the angle subtended by it any point on the remaining part of the circle.
Which one of the following is correct in respect of the above statements
Statement 1 → Statement 2
Statement 2 → statement 1
statement 1 = statement 2
Neither statement → statement 2 nor statement 2 → statement 1
To solve the question, we need to evaluate the two statements provided and determine their correctness and relationship.
1. Analyze Statement 1:
- The first statement claims that the opposite angles of a cyclic quadrilateral are supplementary.
- A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle.
- According to the properties of cyclic quadrilaterals, the sum of the opposite angles is indeed 180 degrees (supplementary).
- Conclusion: Statement 1 is True.
2. Analyze Statement 2:
- The second statement asserts that the angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the remaining part of the circle.
- This is a well-known theorem in circle geometry known as the Angle at the Center Theorem.
- If an angle is formed at the center of the circle (let's say angle AOB), and the same arc subtends an angle at any point on the circumference (let's say angle ACB), then angle AOB is indeed twice angle ACB.
- Conclusion: Statement 2 is True.
3. Determine the Relationship Between the Statements:
- Now, we need to check if there is any relationship between the two statements.
- Statement 1 discusses properties of cyclic quadrilaterals, while Statement 2 discusses angles subtended by arcs in a circle.
- There is no direct relationship between the two statements; they are both true but pertain to different properties of circles and quadrilaterals.
- Conclusion: The two statements are not related to each other.
4. Final Answer:
- Since both statements are true but not related, the correct answer is that neither statement 1 is related to statement 2, nor statement 2 is related to statement 1.
- The first statement claims that the opposite angles of a cyclic quadrilateral are supplementary.
- A cyclic quadrilateral is a four-sided figure where all vertices lie on the circumference of a circle.
- According to the properties of cyclic quadrilaterals, the sum of the opposite angles is indeed 180 degrees (supplementary).
- Conclusion: Statement 1 is True.
- The second statement asserts that the angle subtended by an arc at the center of a circle is double the angle subtended by the same arc at any point on the remaining part of the circle.
- This is a well-known theorem in circle geometry known as the Angle at the Center Theorem.
- If an angle is formed at the center of the circle (let's say angle AOB), and the same arc subtends an angle at any point on the circumference (let's say angle ACB), then angle AOB is indeed twice angle ACB.
- Conclusion: Statement 2 is True.
- Now, we need to check if there is any relationship between the two statements.
- Statement 1 discusses properties of cyclic quadrilaterals, while Statement 2 discusses angles subtended by arcs in a circle.
- There is no direct relationship between the two statements; they are both true but pertain to different properties of circles and quadrilaterals.
- Conclusion: The two statements are not related to each other.
- Since both statements are true but not related, the correct answer is that neither statement 1 is related to statement 2, nor statement 2 is related to statement 1.
Similar Questions
The angle subtended by an arc of a circle at the centre is double the angle subtended by it any point on the remaining part of the circle.
View SolutionTheorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
View Solution
Knowledge Check
- Question 1 - Select One
Which of the following can be the angle subtended by a minor arc at the centre?
A100∘B220∘C180∘D270∘
Angle subtend by an arc at center is double the angle subtend b it at any point on remaining part OF circle||Angle is a semi circle is a 90 ||Example ||Congurent arc|| Equal arc||Cyclic quadrilateral
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionShow that any angle in a semi-circle is a right angle.
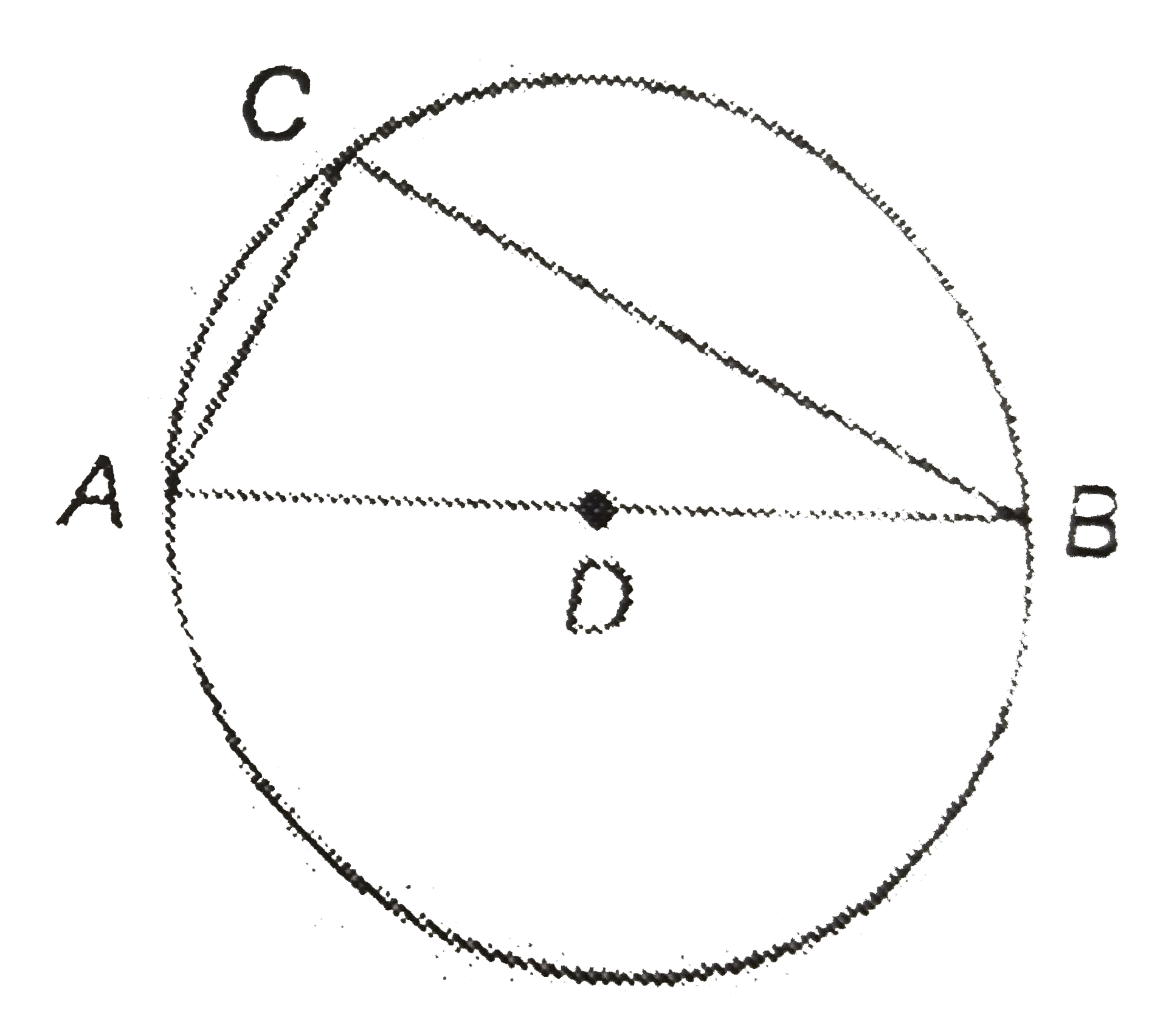
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
 View Solution
View SolutionTheorem:-5 (i) The degree measure of an arc or angle subtended by an arc at the centre is double the angle subtended by it at any point of alternate segment. (ii) Angle in the same segment of a circle are equal (iii) The angle in the semi circle is right angle.
View SolutionGiven an are PQ of a circle subtending angles POQ at the centre PAQ at a point A on the remaining part of the circle. We need to prove that ∠POQ=2∠PAQ.
View Solution

